Bombeとかいうゲームについての手記 その16

このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。

今回検討する盤面はこちら。

盤面自体はあんまり難しくないはず。

0,0,0という組み合わせがあるのが問題。それさえなければ……。

なんかこの絵面に見覚えが……。

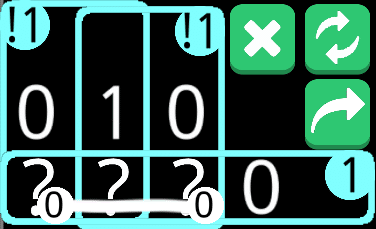
なんだかそのものズバリなルールが設定してあった。これで解けないのは1ではなく1-でも成り立つから。
もう一つやりましょう。

1/3の選択肢を!1で消していることが重要で、それによってaだけで爆弾の個数を調整する際には3であることを強制している。それぞれの範囲のみに含まれるマスが無いというのもポイントか。

これは大丈夫だが、

ψ以下にすると無制限になるらしい。もうよくわからんな。でも多分探索に時間がかかりすぎるようなせいなんだとは思う。

2値で確かめてみたところこの様になりました。

そしてそれは正しいらしい。だからこのパターンは成り立つんですね。
一応考え方を示すと、まずbに爆弾が少しでも入ろうものならばχ+ψという爆弾の最低個数に到達できないため不可能。だから具体的にはcとdに必ず、すべての爆弾が入らないとダメ。

あれ、でもこれ元の盤面解けてないような……。

変換時になにか間違っている。ここまでなら解けるルールであるはず。

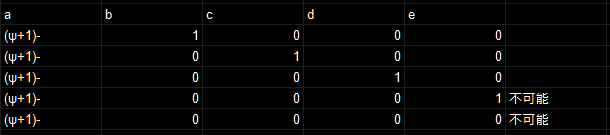
aはどこに入ろうともあまり個数の指定自体は変わらないが、b,c,dに爆弾が入らない場合は不可能である。なぜならば、b,c,dに爆弾が入らない場合、最低でもχ+ψの個数を満たさないといけない。その場合aのマス数がψ+1までであることを鑑みればψ個またはψ+1個であるだろう。ψ個入った場合に、χは0である。そのときにχ+ψ+2は満たせない。χが0である場合は!χ+ψも!ψである。そのためこの場合はすべてが不可能である。

どのようなパターンであっても、とにかくb,c,dに一つしか入らない。2つ以上入っても先程と同様にχの許容値が変わるだけでψに都合の良い数字を設定すると!χ+ψと矛盾する。

また、aのマス数が増えると今度はκ部分の下げられる次数が減る。

この場合はb,c,dには1つも爆弾は入らないということ。結局合計でa,b,c,dの合計の爆弾がψ+2までであればκ-のみに含まれる範囲は(κ-((ψ+2)-(aのマス数)))-であることが確定するということだろう。

わかったような、わからないような。ちなみにここの+2という値はχ+ψ/χ+ψ+2の2であろう。多分。確証はないけど。