Bombeとかいうゲームについての手記 その29
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
そろそろ盤面を見て考えていくのも辛くなってきたので、今まで作ったルールを改めて見てみようと思う。特に雑に作ったルールを。
雑だなあ、これいるのかなあなどと思ったものはすべて加速マーク、あるいは炎上マークがついている。具体的には最適化不足と思われるものが加速マーク、重すぎたり適用回数が少ないものは炎上マークとしている。

最初のルールはこれ。初期に作ったやつなのでかなり作りが甘い。まず右上のχ+2から2個あふれるのが確定している。2個溢れたときは確実に1-と1にそれぞれ1個爆弾が入る。よってまず1は1-に拡張可能である。
次にあふれる個数は他の領域の爆弾の個数と一致していればよいので、右下と左上の爆弾の個数は文字化できる。
さらに、右上の爆弾の個数はあふれる系なので、以上でもよいはずである。つまり、

2ルールのあふれる系の基本形を元にした基本的な3ルールのあふれる系である。なんでこんなの残ってたんだろう……。

次のルール。これは考えるのが面倒で最適化不足としていた、否定形の初期に作ったルールな気がする。考え方は簡単で、!2の範囲内に1が入っているのであれば、残りのマスは当然!1となる。ということ。ここでは2マスに対して0/2としている。

これが意味合いとしては正しい気がする。

既に存在していた。じゃあこれは数字が指定されていて軽いだけで意味ないので廃止。

このよくわからないor3のルール。これも考え方は簡単で、左の最大がχ+2で右の最小がχ+4なので、右のみに含まれる範囲には2個以上の爆弾が確定するというだけ。
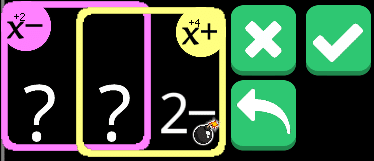
こういうことなので、

こうなって、

こう。このルールないの!?

なんだか絶妙に縛りをつけているようなルールがあった。これはダメです。いらない。いま最適化したほうが上位互換です。

これも考え方は簡単だが、最適化検討はちょっと難しいかも……。
偶数領域と偶数領域が重なっているとき、重なり合う範囲内が偶数個の場合、やはりそれぞれのみの領域の合計も偶数である。
何故ならば、偶数+偶数は偶数であるのに対して、偶数+奇数は必ず奇数であるからである。仮にbを奇数とおくと、a,cはどちらも奇数でなければならない。その場合でも2*が成り立つ。
じゃあbに対する2*という制限はなんで入れたんだろう……。(自問自答)
適用が多すぎて重かったのかな……。しかもこれ文字でも成り立つな……。

文字化した場合は爆弾個数が奇数である場合も存在するが、どちらにしろ上記箇所の合計は常に偶数。
偶奇両対応にしたら何個か追加で問題解けた。しかもクソ軽くなった。最適化って大事なんだなぁ……。

意味わかんない。どういうルールこれ……。

しかもすごいCPUスコア悪い。私のPCに負担をかけるな!(逆ギレ)
これあれか、多分ψ-のところが0個でクリアできるやつなんだろうな。さっき最適化してたルールの応用で、χ+とχ-が重なっているときはbがχ。故にχ-側には爆弾が入らないので、ψ-は実質0個。これはさっきのルールで概念的には全部カバーできてそうな気はするが、3ルールだと違うんだろうか。
うーん、無いと思うけど……。この場合で確定しないのはaにどのくらい爆弾が入るかということなので、得られる結論がψ-であれば不要な気がする。

と思ったら必ずしもそういうわけでもないらしい。んーーー?


bに確定しているのはχ個以下だった。χ+側は0+であることがわかる。(つまり何もわからない)


では何故ψ-が成り立つのか。ここで検討しているルールが入っていることは少なくとも下段右には最大数の爆弾は入らないということだけ。

いや最大個数はいるんかい。ルールを作ったときの私は何を考えていたんだ?

こうなんだからそりゃそうじゃない?じゃあこれで解ける場面は存在しなくない?いや違うか。多分ψ-をより狭い範囲で表現できるのが重要なのかもしれない。

これ作って大丈夫なやつかな……。とんでもなく適用されたりしないかな……。
0-は必要ないので、ψに1足していい。また、ψ-に対して残マスがψマス以下の場合は必要ない情報なのでそれもいらない。

こんな感じか。

あっ、まあまあスコアがいい!そしてこれは概念拡張的なルールなのでそっちに振り分けておく。
これって+の方面にも適用できないだろうか?……できないな。ある個数以上の範囲について、その範囲の中の特定のマスが常にある個数以上ということはありえない。

またおんなじようなのが来たぞ……。何個あるんだこれ系……。

χ/χ+1はχ+に書き換えられるので、下位互換になる。
マス数?であるので0でも対応できるかつ、0の場合のルールも別途ルールで示されている。


だからこれらのルールはいらない。
Bombe Rules (5):
💣⠨⢵⠯⣽⡣⡂⣯⠺⠅⠱⠂⠅⠄⠀⢔⠃⡻⠢⡲⡵⡬⡥⡧⡲⡯⡵⡰⡡⡵⡳⡥⡤⡲⡩⡯⡲⡩⡴⡹⠶⠶⠰⠴⠸⠬⠶⠸⠰⠹⠱⠹⠷⠳⠷⠱⠳⠱⠵⠸⠴⠸⠶⠵⠸⠴⠰⠬⠳⠰⠵⠲⡝⡽⠚⢰⠠⡉⡄
⢪⠵⡵⡙⢐⠐⠑⡊⠋⠏⣧⠙⠒⣊⠰⢖⢮⠬⡅⣁⠠⢀⠇⣩⣁⡰⠃⠔⣶⢟⠁⣆⡧⠓⠲⡻⡴⣠⠫⢲⢔⣁⢁⠩⡅⢾⣞⡆⠬⢟⢘⠜⣘⣨⢝⡁⠄⣡⠇⠶⢛⣥⡄⠂🛑

1個以上溢れ出す以外に特になにもないルール。なんで次数上げたまんまなんだろう。
1個でも爆弾が入ったら0が否定されるので、これは成り立つのだが、1個以上入ったときに否定されるのは0だけだよなぁ……。

これでWrapperできてない?

これもあるんだし。

これもあるので。大丈夫そうだな?消そう。

偶数個で3マス以内ってことは2なんじゃないの?

まあ2*のほうが範囲が広いようで実質変わらない。ってか!1で2マス以内ってことは0/2なんじゃないの?

あるやん。じゃあこれも廃止で。

なんかこれもさっき見た形と似てるなぁ……。
まずこのタイプは+と-になると思う。

なった。χ個が溢れるが、溢れ先がχと1-に確定しているので、それぞれχ-1個、1個、もしくはχ個、0個入ることになる。
前者であれば、1-から言って下段左はクリアできる。後者であれば、χ-から言って下段左はクリアできる。故に常に下段左はクリアできる。

まあまあ実績もあるしなんだかうまくできてそうな気はするが、1-が固定なのが気になる。これって例えば2-では成り立たないのか?
2-としたとき、溢れ先がχと2-に確定しているので、それぞれχ-2個、2個、χ-1個、1個、もしくはχ個、0個入ることになる。これだと3パターンに増えるが……。下段左について……
χ-2個、2個のとき
2-から言ってクリアできる。
χ-1個、1個のとき
χ-から見て1個入る可能性がある。2-から見ても同様。
χ個、0個のとき
χ-から見てクリアできる。
なるほど、ちょうど間になる方が問題なのか。ということは1-にしなければ文字化できるのかもしれない。

うーん、なんかちょっと違う気がする……。これは完全にそれぞれの個数溢れるから、上段真ん中と下段右が確定してそれで他には爆弾が入らないというだけ。
π=1のとき(χ+ψ)+であった部分が(χ+ψ+1)+になってしまうので、絶妙に範囲が違う。

元々のルールで同じ結論を得ようとした場合、該当箇所が引っかかる。でも0のときは対して意味ないんだよなぁ……。

こうすれば同じになる。κとπの合計値以上であることを強制される形になる。1-であることが固定になっている場合、何故下段左だけクリアできてしまうのか。
適当に代入してみるか。
χ=1 : 1-, (ψ+2)+
χ=2 : 2-, (ψ+3)+
χ=3 : 3-, (ψ+4)+
そうなんだよな……結局χ=0のときって意味ないんだよな……。

そうなるとこうなる。そう考えてみると別にいいのか?κとπの合計値以上であることを前提としても……。いや!こうか!

これで前述の通りπ=0のときに対応範囲が同じ。

更に下段真ん中もあっても良い。長々と考えたかいがあった。

んー……。0のとき当然に0で、1のときbは奇数個ではないので当然0となる。
これはこれ以上最適化できないのでは。0/1以外にも適用できるのか?
でもχにしちゃうと1/2とかが普通に成り立たない。これはこれでいい気がする。あ、あと0/3とかもどうだろうか。

これも成り立つだろう。うん。意味あるのかなこのルール。ありそう。多分。

これについては、

この形でも成り立つのだが、全く意味がない。何故ならば、
2*∋2+2*∋4+2*……∋2*+2*
同様に、
1+2*∋3+2*∋5+2*……∋1+2*+2*
要はすべての偶数と奇数をこの2つが含んでいるので全く意味がない。

そのまま要見直し対象から外す。

なんでやねん。

今回の冒頭で書いたこれと同じ。これも削除。

これは実質χ+1/χ+2が(χ+1)+に書き換えられるのでこれもいらない。

これも0/1が1-と同じなのでやっぱりいらない。

なんかこれもさっき見なかったか?そっちは2*のほうか。というかこれはもうbは0/2というだけなのでは。でもこれなんでも成り立つのでは?

何でも成り立つやんけ!

これも成り立ちはするが……この場合、1マスについて1-が確定しても何も確定できてない。0/2までにとどめておくのが良かろう。多分。

クソルール臭がする。

そうだよなあ!だって、
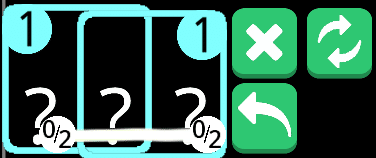
こうだもんなあ!許せねえ!ちなみにこのルールはいるのだろうか。1同士でしか成り立たないけど。

まあまあ強そうなので残しておく。

んん?……うん……うん?
いや待ってほしい。これは3つ目がいらないのでは。

えっ、違うのか?そういうことではないのか……。
他の領域に進出していって確定するのが重要なのか?
まあ3ルール必要なところを2ルールで解けるようになるならば有用か……。
一旦ここらへんで区切る。次回以降も多分続く。
