Bombeとかいうゲームについての手記 その27
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
今回検討する盤面はこちら。
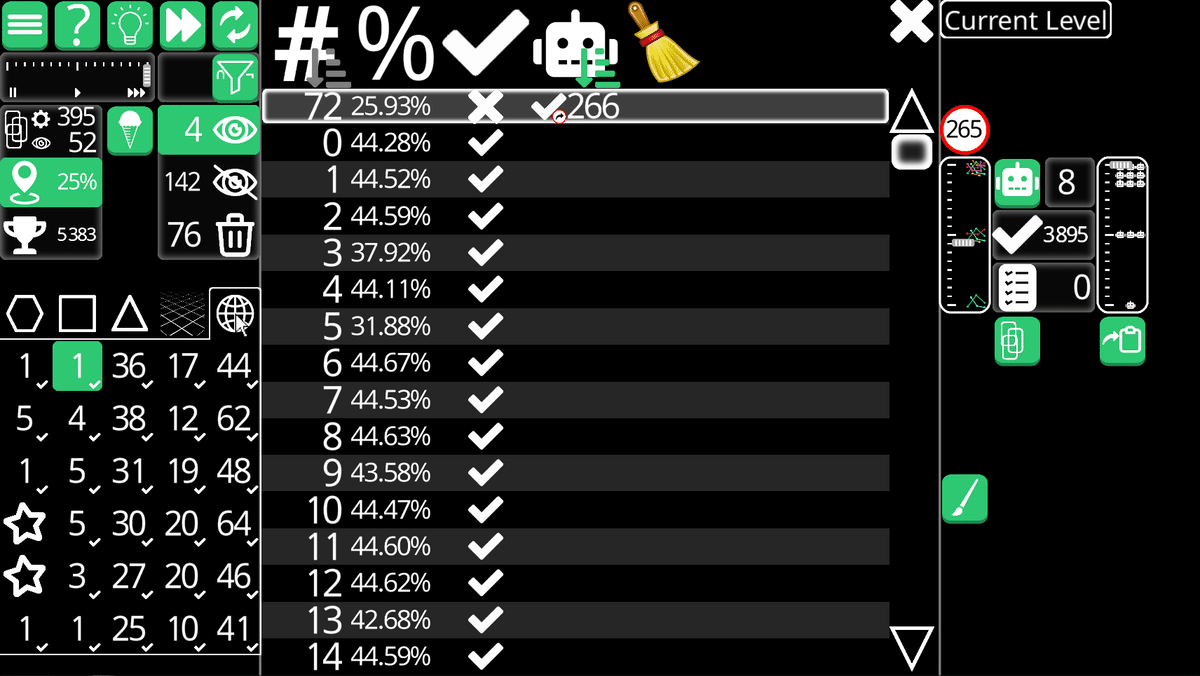

わかるけどわかりたくない盤面。これは多分4ルールから抜け出せないんじゃないかな……。

左上の0/3を0とすると、もう一つの0/3も0となる。1/4についても4がありえなくなる。これはマスが爆弾の可能性があるマスが、4マス以上残っていないからである。
左上の0/3を3とすると、もう一つの0/3も3となる。1/4についても4がありえなくなる。これは既に1の範囲の爆弾が埋まっているからである。
故にこれらの爆弾の個数は001もしくは331のパターンしか無い。
001のとき、1/4のみの範囲に属するマスは爆弾ではない。
334のとき、1/4のみの範囲に属するマスは爆弾ではない。

多分こういうことになるんだろうが、0/3の範囲のマス目の散らばりようが様々すぎて……。

囲った部分のマス数の総和が一定以下であれば多分成り立つ。たまに登場する、◯/◯+XのXの部分のマス数が関係しているやつ。
……いいか、文字化しなくて……。これ文字化しても結局、あんまり一定以下であれば成り立つ条件のせいで対して汎用化できないからな……。
次の盤面。




まあこういうことでしょうな。こんなルール作ってなかったっけ?
つくって……ないなあ……。

2/3と1-のパターンについての結果。
左の爆弾の個数からして、χ個以上あふれることが確定している。ということはcには当然爆弾が入らない。


bは当然χで、χ+2が該当することは絶対にない。

わかったことをすべてルールにしてみたが他のを使っているのかどうかは謎。
次の盤面。



これもすごく簡単でわかりやすいのにルールを書きたくない。3/4に着目するとどこかに1マス爆弾でないますを確定させると盤面の内訳が確定する。
爆弾でないマスが1-の範囲内であるとき、1/2は2個の爆弾を満たしている。そのため、1+と被る範囲は爆弾ではないので、1-と1+が被る範囲内に爆弾が一つ確定する。故に1-のみに属する範囲には爆弾は存在しない。
爆弾でないマスが1/2の範囲内であるとき、1/2の範囲内について爆弾が1つはいっていることになる。1-の範囲には既に爆弾が含まれているため、残りのマスはすべて爆弾ではないはずである。故に1+の範囲について爆弾が入る余地が残っているのは1/2の範囲と被っている部分のみであり、1/2は結局2であることがわかる。
3/4のみに属する範囲のマスが爆弾でない場合、1/2は2を満たしており1-については残りのマスが爆弾ではないため、1+の範囲に爆弾が存在できない。よって不可能。
つまりどちらにしても1/2は常に2であり、1-のみに属するマスは常に爆弾が入らない。

このくらいまでは文字化できたがやはり軸は1/2と1-の関係性だろうか。3/4であった部分については2+ψ個爆弾があふれるいつものパターンである。それが1-経由で1+に届くか、1/2経由で1+に届くかの違いなのだろう。1/2も常に2だったのでそこら辺を少し整理したい。

このままだと成り立たないので、つまるところこの反例のパターンのみ否定できれば良い。……結局4ルールなのでは?私は考えるのをやめた。

それでもまあまあ解けている。うーん……もうちょっと汎用的になってほしいなあ……。
もう1盤面。





01の組み合わせか32の組み合わせしか無い。1/4は内訳から見るに4ではありえず、どちらにしてもb,cに爆弾があるため該当箇所は爆弾ではない。
これ文字にできないなあ……。
0/3と1/2の関係性を1/4の存在で一部で補強して可能性が一つに収束するのはわかるのだがそれが文字にならない。なんで。もう少しうまいやり方があるのだろうか。
