Bombeとかいうゲームについての手記 その36
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
今回検討する盤面はこちら。


5ルールからの圧縮方法全然わからん問題の解決策となれるか。
整数だけなので、だいぶ情報量が多いはずだが……。


偶奇もルールにできなさそうだし、うーん……。差分が2*とかもルールには奈ならなさそう。やっぱり先に答えがどうあるのかを調べるか……。
これ思ったよりパターン多いな……。
一つわかることは、7個の爆弾について8マスあるから、どこが爆弾でないかを確定させていけばおそらく答えは得られるのだが、つまりそれは8通りあるということである。面倒。


色々弄ってたら4ルールのバージョンを見つけてしまった。
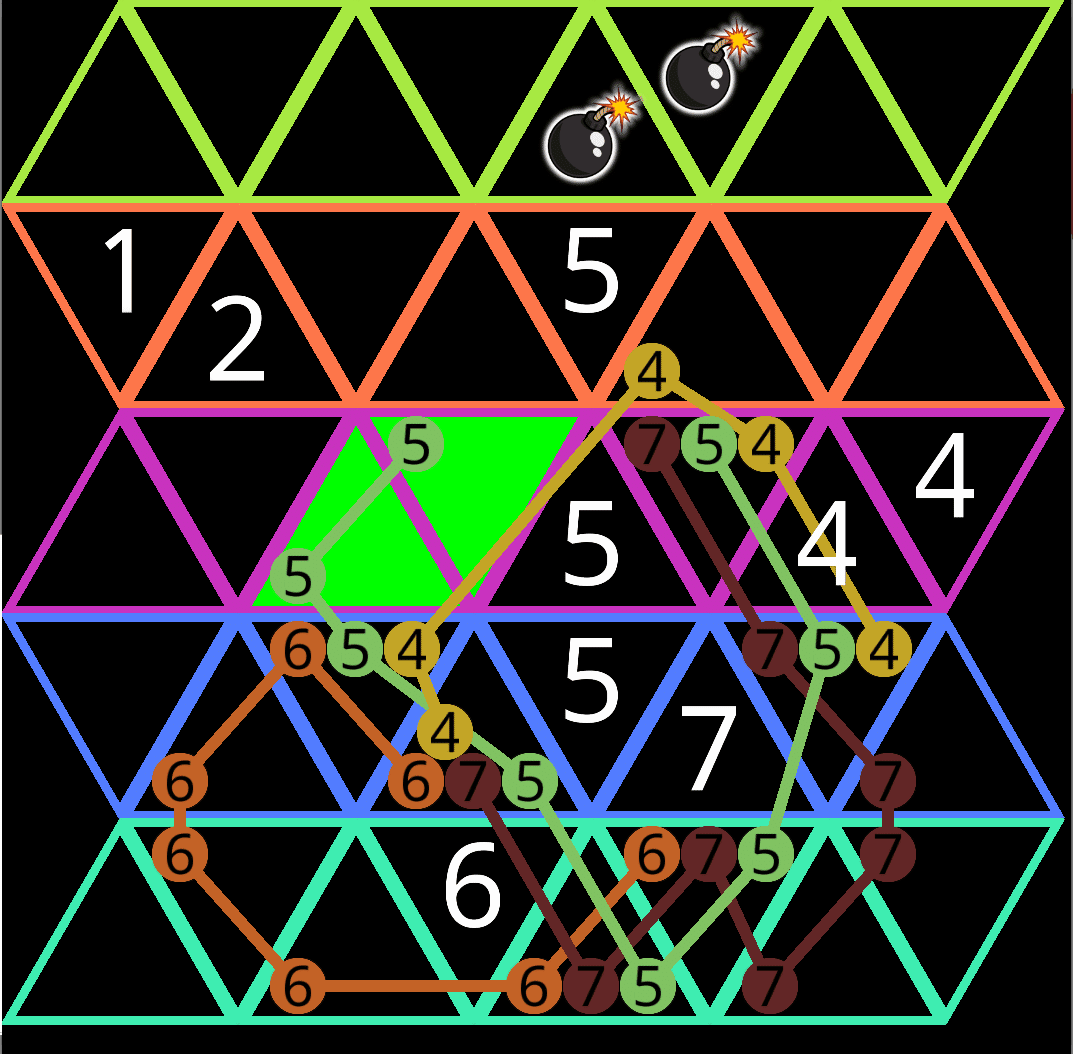

どうやら該当箇所はクリアできるセルらしい。それはともかくとして。

これは前に作ったこれ系だと思う。溢れる方の合計が受け入れる方の合計と一致している系。これを作ったときはそれぞれの合計値以外に相関がなくてルール化できなかった。しかもこれは次数が高いので尚更そう。

文字で表せるタイプはこっち。これは溢れる個数と受け入れる個数がそれぞれ一致しているだけ。それぞれの合計も、もちろん一致する。

今回のはそれの亜種で、溢れる方と受け入れる方が一致はしていないが、あふれ先がほとんど5に偏っているのがポイント。溢れる個数だけ考えれば7個溢れるが、受け入れ先はすべて5の範囲内なので、合計は5個である。つまり合計の溢れる爆弾の個数が、4+3,3+2,2+1,1+0……7,5,3,1の個数があり得る。それぞれ、あふれ先について真ん中列に入る爆弾の個数が0,1,2,3個の場合である。今回は5に確定しているので、それぞれ真ん中に溢れる個数は1個以上に確定する。……もしかしてこれが新ルール、欠けていた視点じゃないか?それは一旦置いておくとして、次のように真ん中の個数が狭まる。

さてここで、下の4の関係性が見えてくる。これも溢れる系だ。

つまりこれは3方面から溢れる系の盤面である。そしてそのすべてが5に集まっている。

わかりやすくするために、0にできるところをすべて0にした。この場合、κから溢れ出した先にはχの範囲しか無い。つまりχの範囲に爆弾3つが確定して、下段左が2個、下段真ん中が1個である。さらに上段真ん中が1個に確定する。……しかしそうすると、実際にはψの範囲に爆弾が足りない。なので実際はこれは不可能で、χ=1以上の場合のみ成り立つ。故に、上段真ん中は2個となる。

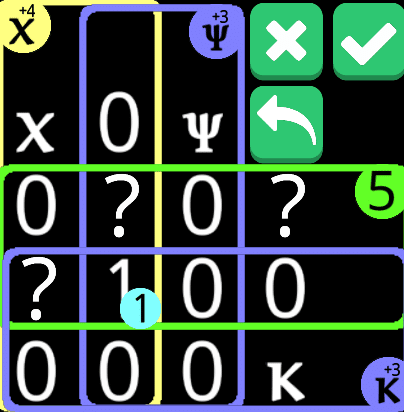


とにかくこのように真ん中の方だけで爆弾の個数が満足されるので、とにかくこれは5についてその範囲のみに該当するマスはクリアできる。
では他のマスに存在を許した場合はどうか?

それぞれa,b,c,dとした。aが0でない時、しかしこの場合はκによって爆弾の位置が決まる。余った部分は確かにaに入れてもいいものの、入れると不可能になる。

bも同様で、κによってχの爆弾が定まるので、b2爆弾を入れる余地が存在しない。ただし、それはあくまで前述のとおりに推測される場合であって、例えばχの数がほかと同等である場合にbに爆弾が入る可能性がある。

次にcは全くbと同様。ただし、少しだけ例が違う。

dに関してもbと同様で、こちらはκから溢れ出す個数が減るので、実質χの範囲の爆弾の位置の確定度合いが少しだけゆるくなる感じである。
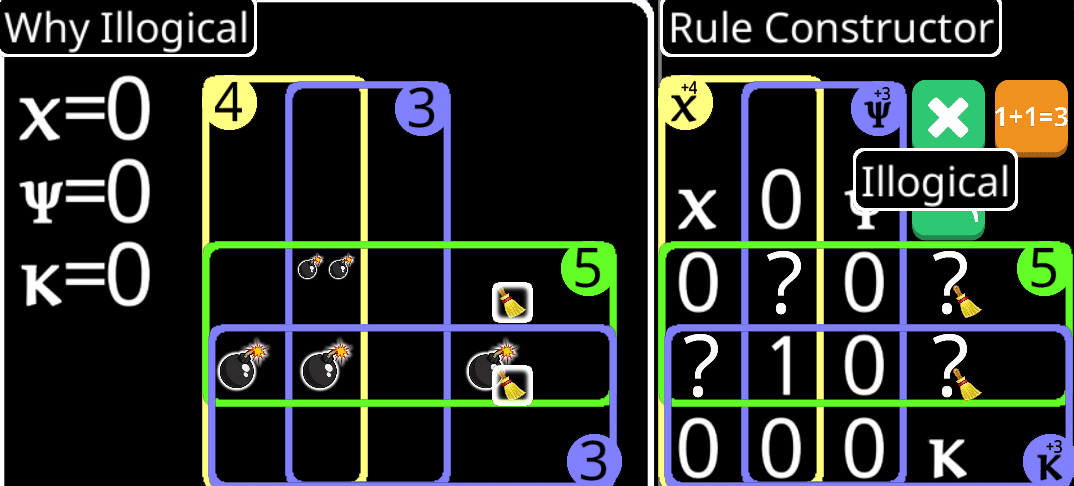
しかしどのパターンにしてもやはり5のみに属する範囲に爆弾は入らない。
この時点で、それぞれ4,3,3個溢れ出しているので、普通に考えれば合計で最大個数は10個になる。ここで、先程書いたように、共通の部分に爆弾を入れることによって、爆弾の個数を減らせる。方程式に表すと次のようになる。
10 - 1*x - 2*y = 5 → x + 2y = 5
xとyは爆弾の個数なので当然、正の整数である。(正の整数ではない可能性がアプデで増えたので正の整数とは言えないのだが、ここでは正の整数とする)
この場合の解は、xとyについて、(x, y) = (1, 2), (3, 1)となる。

実際には(1, 2)は盤面の制約上存在しない。(yは最大1まで)
故にこの場合のみが解となり、成立することになる。

さて、では5は何故この数なのかと言うと、これはyが1である場合に許される最小の数が5だからである。方程式上は、仮にyが2まで許されるのだとすれば、最小の数は4に。3まで許されれば3になる。

しかし実際には最低値は4である。

これは方程式上は無制限に爆弾の個数を圧縮できるようになっているが、実際はχから溢れ出す個数が4つであり、それを下回ることはできないからである。
そのくらいにしておいて、
>>……もしかしてこれが新ルール、欠けていた視点じゃないか?
とか言っていたところを考察する。
でもよく考えたら、3つ溢れる系のあふれ先マスを適当に選んだら、0~3になるのは当然だな。じゃあ別に新発見でもないか。0を排除できたのは何故だったっけ?他のマスの都合で0にすると個数の都合が合わないのか。
でもこれ同じ盤面ならクリアできるセルが見つかってるわけだしいらんよなぁ……。やっぱいらんのか……。
結局今日も5ルール圧縮できない問題は片付かなかった。答えはわかるのに……。
