[高校数学] 一度分かれば忘れない「数列の和」のイメージ図

とする。

■等差数列の和

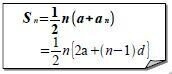
初項；a, 公差；d　とする。幅が１で、長さが a, a+d, a+2d ┈ のテープを並べると段々の台形のような形になる（下の緑の部分）。

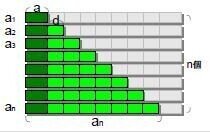
それを180度回転させて（灰色）、組み合わせてできる長方形の面積　

が求める和の２倍、２Sなので、長方形の面積を求めて２で割ればよい。つまり、台形の面積の求め方と同じ考え方で、

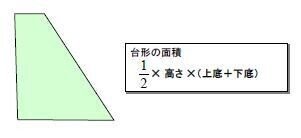
ただし、高さ＝n, 　上底＝a, 下底＝a↓n　とすれば求められます。

■自然数の数列｛n｝の和

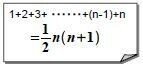
等差数列なので、上と同じ考え方。下の図では、青い 1x1 のマス目の数です。

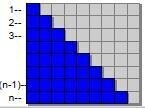
高さ＝n, 　上底＝１, 下底＝n　の台形の面積を求めるのと同じです。Σ公式で表すと、

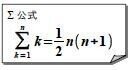
●教科書でおなじみ、「２S法」

☐奇数の数列｛2n-1｝の和

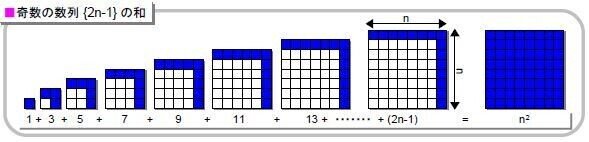
覚える必要はありません。図にすると面白いから取り上げただけです。Σ公式で求められます。

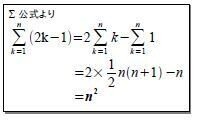
２S法でも求められます。↓

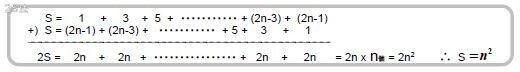
■２乗数の数列｛n＾2｝の和

↑この公式です。１～n の数を使った和で表すと↓

となり、正三角形に並べるとこうなる。

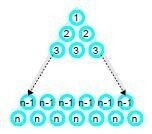
向きを変えた正三角形を２つ作り、↓

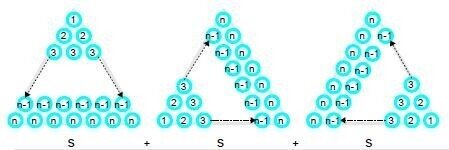
それぞれの同じ位置の数を足すと、2n+1  が並ぶ正三角形ができる↓。これが、３S を表す図！　

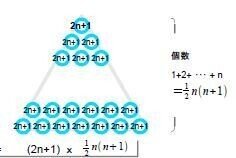
個数は 1+2+3+⋯+n  なので、この図と

３S＝(2n+1) ｘ1／2  n(n+1)　であることを覚えておけば、公式を忘れてもすぐ作れます。　 まとめ

■３乗数の数列｛n＾3｝の和

印刷用PDFダウンロード