
学ぶことは大人の贅沢
こんにちは!
20年くらい前にハマって読んでいた書籍の続編を今頃買いだしたBFT名古屋支店・インフラ女子(?)のやまぐちです。
中学一年生の甥っ子から「問題の意味が全くわからない。ヘルプ!」と連絡が来た数学の宿題。簡単にまとめると
正二十面体の各頂点から切り取ったあとの立体の辺の長さがすべて等しくなるように正五角錐を切り取るとして、その後の立体について次の問いに答えよ。
(1)正五角形の面の数を答えなさい。
(2)正六角形の面の数を答えなさい。
というもの。・・・はい?というのが最初に思ったことでした。
しかしこれが意外と面白くて子供の勉強を見るのって復習&深く知るいい機会だなと思ったので、今回は正二十面体と切頂二十面体(せっちょうにじゅうめんたい)について調べた内容を書いていこうと思います。
まずはしばらく考えて甥っ子へ返した内容から。以下が正二十面体です。WikipediaのGIFは回転が速いです。
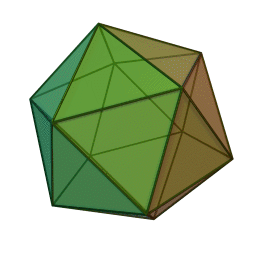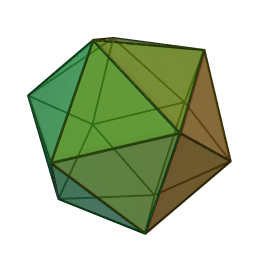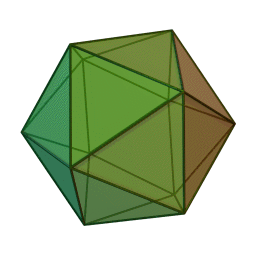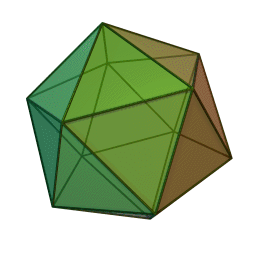
これの各頂点から正五角錐を切り取ると以下の切頂二十面体になります。「せっちょう」って全然読み慣れません。相変わらず回転が速いです。
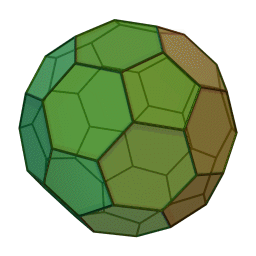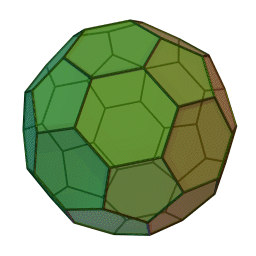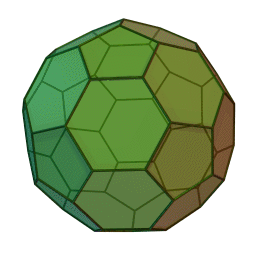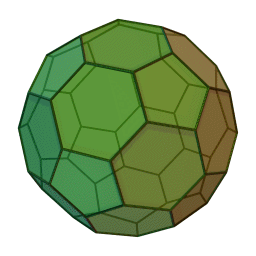
(1)正五角形の面の数を答えなさい。
「頂点から見ると5つの面が集まってるじゃん?頂点から正五角錐を切る取るって言ってるから、正五角形の数は切り取った正五角錐の数、つまり頂点の数と同じになるんじゃない?」
(2)正六角形の面の数を答えなさい。
「元々正三角形だったけど、頂点で正五角錐を切り取られたら辺が3つ増えて六角形になるんだから、元々の面の数と同じになるんじゃない?」
立体が苦手な私から言える最大限の回答は甥っ子にわかりにくかったらしく、結局数学の先生のわかりやすい図説で理解したらしいです。
正多面体ってなんだっけ・・・
![]()
問題と一緒に正多面体とはという画像も送ってくれて、そこには5つの立体が写ってました。
すべての面が同一の正多角形で構成されてあり、かつすべての頂点において接する面の数が等しい凸多面体のこと。正多面体には正四面体、正六面体、正八面体、正十二面体、正二十面体の五種類がある。
エンジニアになって「疑う」というクセがついてしまった方も多いと思います。え?なんで5つしかないんだろう?今後出てこないの?と疑問に思った私への回答はきちんと数式で証明されていました。
数学が苦手な私はきっと当時そんな疑問も浮かばなかったことでしょう。
正二十面体を見て思ったこと・改めて知ったこと
![]()
すべらない話のサイコロだ!
正二十面体を見た瞬間に問題そっちのけでそう思っていました。
番組を見ていてうっすらと「あれって何面あるのかなー」なんて思っていましたが、思わぬところで回答が出てきました。今まで番組では正六面体(普通のサイコロ)、正八面体、正十二面体、正二十面体が主に使われているそうです。出場される人数はこの面の数から★を引いた数になるので、出場人数からどのサイコロが使われるのか予想できるという何にも使えない能力を得ました。
あともう一つ、正二十面体を見て思い出したのがファージ(正式には「バクテリアファージ」)の頭でした。
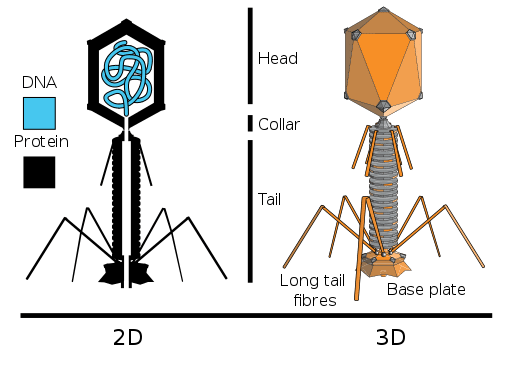
Autor:Adenosine、CC by SA-2.5、ウィキペディア(Wikipedia)『ファージ』より
高校の生物で習う大腸菌に感染するT2ファージの話は覚えている方もたくさんいらっしゃると思います。このバクテリアファージの頭にはRNAやDNAが詰まっているのですが、最大限効率的に格納できるのが二十面体だそう。
ハチの巣がなぜ正六角形なのかということを学生の頃に習ったのを思い出しました。多面体の中で最も外接球(または内接球)の容積が最大になるのが正二十面体なんですね。なるほど。
サッカーボールは切頂二十面体!
![]()

サッカーボールがどうして六角形と五角形なのか、別に調べるほどではないですが学生の頃からずっと疑問でした。それこそ六角形のハニカム構造が最も衝撃に強いのにどうしてサッカーボールには五角形が入っているんだろうかと。もちろんすべてのサッカーボールがこの構造ではないのですが…。
問題の「正二十面体の各頂点から切り取ったあとの立体の辺の長さがすべて等しくなるように正五角錐を切り取」った面がサッカーボールの黒い部分ですね。
正二十面体をより球体に近づけたものが切頂二十面体。え?じゃあどうして他の球技の球、例えばバスケットボールやテニスボールや野球のボールはあのデザインなんだろうか。…と色々調べていたら全然記事が終わらないので気になった方は調べてみてください。それぞれのスポーツには歴史があるんだなぁとそれはそれで興味深かったです。
終わりに
![]()
今回は中学一年生の数学の問題を例に、既存の知識から更に深く学ぶ楽しさを記載しました。
「大人の贅沢」と表現したのは学生の頃問題を目の前にした時にこのような学ぶ楽しさを実感することが私自身できていなかったからです。知っていることの範囲が狭かったのは反省すべき点ですね。
こじつけみたくなりますがITの技術は、
① 言葉の意味を調べながら何となく大まかに捉える
② 何度も同じような表現を見聞きして「知っている」状態になる
③ 実際に手を動かして体で覚える・理解する
④ 他の技術を見聞きすることで更に理解が深まる
というプロセスで理解することがよくあると思います。しかし日々の答え・成果を出すことに追われてしまうと、その技術の本当の面白さを実感する時間を持ちにくくなりがちです。
これからも毎日がその日の仕事でいっぱいいっぱいにならず、新しく学ぶ時間と心の余裕をもって過ごしていきたいと改めて感じました。
誰得な長い話になってしまってすみません。
ここまで読んでいただきありがとうございました!
