ランゲルハンス島の眠りと目覚めと協調性【統計力学の不思議世界探索】#28
ランゲルハンス島(pancreatic islets)とは、すい臓(pancreas)の体積のうち約5%を占め、島のように散在する内分泌腺の細胞群である。主な機能としては、血中の糖分濃度の変化に反応してβ細胞がインスリンを分泌し、全身の細胞が健康に活動できる範囲に血糖値を調整する。
すい臓の残りの約95%は外分泌腺で、消化酵素を十二指腸に送り出す。(血液が巡る範囲が"内"で、それに対して腸管の中は"外"とみなす。)
ここまでは、生物の教科書や一般教養のレベルだと思うが、本論文を読むと、インスリン分泌だけでなくこんな興味深いネットワーク転移が毎食後すい臓で起こっているのか!と感心するし、こんなデリケートな仕組みだから糖尿病って起きやすいのかとも考えられる。
統計力学の不思議世界探索、今回紹介する論文はこちら。
Critical transitions in pancreatic islets
ランゲルハンス島の臨界相転移
2410.17756 (arxiv.org)
(※あくまで現象としての興味深さに触れるだけで、糖尿病の治療や予防などには一切触れません。)
本研究では、膵臓の新鮮組織スライス中の無傷のランゲルハンス島において、グルコース濃度をゆっくりと増加と減少をさせて反応を見る。知られている反応閾値である約7mmol/Lの上下を行き来させ、β細胞の活性は細胞膜の電位と細胞内のカルシウムイオンの変動で検知する。(論文ではmmol/LをmMと略記している)
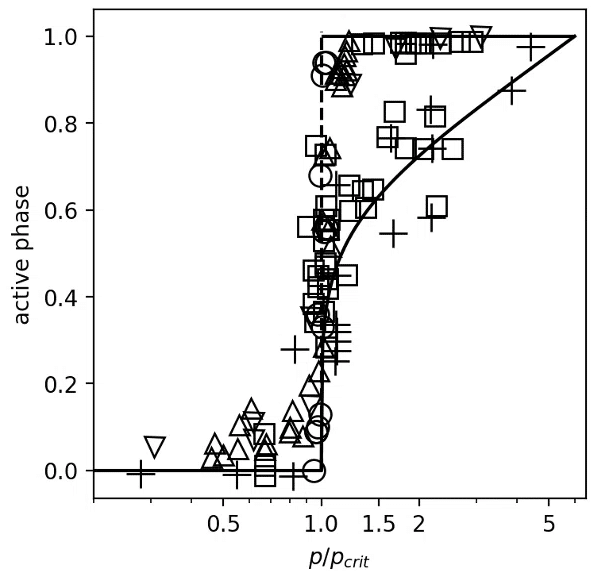
7mmol/Lで急激にβ細胞が活性化する様子を捉えたデータがまず図1。

□:本実験のスライス、+,○:先行研究[14]、▽,△:Kir6.2変異を持つもの
下:活性化遅延(β細胞が活性化し始めてからある値まで達する時間)
横軸は最終的なグルコース濃度、縦軸は活性化時間でこれも最大値を1に規格化している。
□,○:グルコース濃度上昇時、♢,△:下降時
まず図1上では、真ん中の点線で表されるようにほぼ垂直に立ち上がるデータ点と、実線のように滑らかに上がるデータ点がある。
この違いは、細胞間コミュニケーションが損なわれていないランゲルハンス島群から採取されたデータでは、鋭いほぼ垂直な立ち上がりが観察される。
一方、細胞間コミュニケーションが損なわれているものは滑らかな立ち上がりとなる。
また図1下では、滑らかな立ち上がりを示すもので活性化にかかる時間を調べた。閾値を超えない6mmol/Lでは何も反応はないが、最終的なグルコース濃度を上げていくと、遅延が急激に小さくなっていく。
この、立ち上がりが連続か不連続かの差に現れる、細胞間ネットワークの違いについてより詳しく見ていく。
各ランゲルハンス島が発するカルシウムシグナルは、膵臓内の灌流によって隣の島を刺激して反応を誘発する。反応のタイミングが近い者同士を"つながっている"とみなして島同士のネットワークを考える。範囲は、タイミングの近い10個までとする。
このつながりは、膵臓内の灌流が単なる拡散ではないために、近い順の同心円ではなく、ある程度樹枝状に広がりを持ったつながりとなる。
この辺りは、都市内の渋滞ネットワークに似ているとも思う。都市交通のボトルネックが都市全体に及ぼす影響【論文紹介】#23|喜多見奈美 (note.com)

上から、カルシウムシグナルの全体平均、グラフラプラシアンの最大固有値、クラスタ係数、グラフラプラシアンの2番目の固有値
図2縦の青線は、左から1番目と3番目が、グルコース濃度が臨界値を通過した時刻、2番目と4番目は活性化と非活性化にかかった時間幅を示す。
まず一番上のカルシウムシグナルは、左側の不活性状態ではノイズ的だが、活性状態になると一定周期で激しく振動する。活性化前半では全体の周期が揃っていないせいでまだ平均としてはノイズ的だが、後半には全体の周期が揃って平均としても激しい振動が見て取れる。
2番目は、グラフラプラシアン(Graph Laplacian)の最大の固有値である。説明は↓こちらのサイトに任せるが、ネットワークのつながりの強さの値と思えばよい。
【ネットワークの統計解析】第7回 グラフラプラシアン・グラフフーリエ変換を簡単に振り返る - Sansan Tech Blog (corp-sansan.com)
閾値を超えると、つながりの数は10で変わらないのにネットワークのつながりが強くなりカルシウムシグナルの振動が同調しやすくなる(下の図4で詳述)。
3番目はクラスタリング係数で、各セルから見たクラスタの大きさの平均値である。これも、活性状態になるとほぼ全体がつながるほどの巨大クラスタが構成されるのが見て取れる。
4番目は特に興味深く、グラフラプラシアンの2番目の固有値は活性化に先立って鋭いピークを持って立ち上がっている。これはいわば、2番目に大きいクラスタのつながりの強さである。最大クラスタが台頭してくるよりも先に、小さめのクラスタが急成長する。そして2番目のクラスタも最大クラスタに取り込まれると、それまであった2番目のクラスタとしての構造は崩れてしまう。

下:グラフラプラシアンの最大固有値と2番目の固有値の比の変化
同類選択性係数(Assortativity coefficient)とは類似した次数のノードとつながるノードの選好性を定量化する係数である。これも説明は↓こちらのサイトに任せるが。
ネットワーク構造の Assortativity とは何か (hirokazaitsu.com)
活性化時には、まず同類選択性係数が上がって、下がると同時にグラフラプラシアンの番目の固有値が上がるという動きがある。
まず同類のものとつながってたくさんの小さいクラスタが成長する段階があり、その次に異種のクラスタとつながって大きなクラスタになっていくという段階性が見て取れる。
ここまで見てきたネットワーク構造の統計量の変化は、単純なネットワークで見てみると図4のようになる。

⑦ー⑥のつながりがなくなり、⑦ー②につなぎ変わる
図4のようなつなぎ変わりが起こると、同類選択性係数 r は1/3から-1/5に急激に落ちる。異種とのつながりも増えたということだ。
各頂点から出る辺の数は変わらないが、このつなぎ変わりによってネットワークの構造が変わり、全体の性質も変わる。全体への信号伝達完了にかかる時間が減り、ネットワークのつながりが強くなる。
このようなネットワークの性質の変化が膵臓全体で起こり、グルコース濃度閾値に対する反応性が高まる。
図1で見たように、細胞間コミュニケーションのない細胞1個1個では、反応の立ち上がりは滑らかである。
ただ、滑らかといっても0.4くらいまでは急激な立ち上がりはある。
0.4くらいの力でもみんなでタイミングを揃えれば全体としては、閾値を超えた瞬間に急激な反応ができるようになる。
全体が総和とは違って急激な立ち上がりになるという、全身の細胞の健康を維持するための驚くべき創発現象が膵臓で毎食後起こっているのである。
(余談)
このタイトルは、一度はどこかで(家庭によっては毎日)聞いたことがあるだろうこの曲と掛けてみました。食後というよりお風呂?
これまたあんまり関係ないものをノリでタイトルにしてしまった気がする。
最後まで読んでいただきありがとうございます。気に入っていただけたら「スキ」ボタンを押したりフォローしたりしていただけますと私のモチベが上がります。内容についての質問や感想もお待ちしております。
また、研究機関には所属せずにやっておりますので、有料ジャーナルのアクセス料程度のサポートをいただけるとありがたいですし、今後の記事の質が上がるかもしれません。どうぞよろしくお願いいたします。
