「関係がない」のに「当てはまる」気がする

今回は，無関連なのに当てはまる気がする，という例について書いてみたいと思います。

どうしてですか

授業をしていて「これまでの研究だと，これとこれはほとんど関連がないのですよ」という話をすることがあります。そのときによく出る質問のひとつは，「でも私の知り合いはこれとこれに当てはまる人なのですが，それはどうしてですか」というものです。

出生順で考える

たとえば，「出生順は性格にほとんど関連しません」ということを考えてみましょう。この論文（The associations of birth order with personality and intelligence in a representative sample of U.S. high school students）では，37万人以上の調査から，出生順と知能や性格との関連を検討しています。

そしてその結論は，
◎出生順と性格との相関係数：0.02
◎出生順と知能との相関係数：0.04
というものであり，調べてみたけれど「ほとんど関連はありませんでした」というものになっています。

ScienceDirect

この著者たちはもっと短いコメント論文も書いています（Settling the debate on birth order and personality）。そこでも，結論として「科学的な証拠は，出生順がほとんどパーソナリティ特性や知能の発達に関連しないことを示している」ということが書かれています。

Settling the debate on birth order and personality

でも

さて，これまでの経験上，このような話をすると「でも私の姉は私とは違ってしっかりした性格で，頭も良いのですがどうしてですか」という質問が出てくることが予想されます。本当にこういう質問は毎年多くて，この手の話をしたときの定番になっています。たぶん，日本中でされているのではないかと。

いないわけではない

その答えは，「関連がないことは，そのような人がいないことを指すのではありませんよ」というものになります。

相関係数0.02というのは，次のようなグラフの状態です。そして相関係数0.02というのは「実質的にほとんど関連が見られない」状況にあります。たとえば，横軸を体重，縦軸を数学のテスト得点としてみましょう。１つ１つの点は，ひとりひとりの個人です。点は500個ありますので，500人の体重と数学の得点がグラフに描かれているということです。

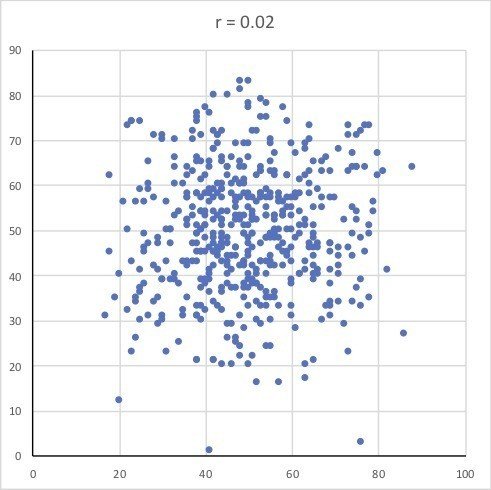
このとき，「体重が重くて数学の点が高い人」（右上），「体重が重くて数学の点が低い人」（右下），「体重が軽くて数学の点が高い人」（左上），「体重が軽くて数学の点が低い人」（左下）が，だいたい同じくらいの人数になります。

「体重と数学の点数との間にはほとんど関連はありませんよ」と言ったとき，「でも私の知り合いは体重が重くて数学も得意なのですがそれはどうしてでか」と質問されたらどうでしょうか。

いてもおかしくない

その答えは，「いてもおかしくありませんよ」というものになるのがわかるのではないでしょうか。その組み合わせだけでなく，他の組み合わせも同じくらいいて，全体的に体重と数学の点数との間に何かの法則があるとはいえない，ということになるからです。

「あることと別のこととの間に関連がない」ということと「この組み合わせの人がいる」ということは，両立しますので，関連がないときにその組み合わせで反論しようとするのはあまりよい反論の仕方とは思えません。

でもやってしまいがちなのですよね。なぜかというと，「関連がない」を「そういう人はいない」と解釈してしまうからではないかと思います。

関連がない

心理学を教え始めたときに学生から色々な質問を受けたのですが「どうしてこういう質問がたくさん出るのだろう」と悩んだことがあります。そのとき，「無関連がどういうことなのかわかっていない学生がいるからだ」ということに気づいたのでした。こういうことに気づくことが，授業をわかりやすくしていくひとつのコツでしょうね。

「関連がない」という考え方はなかなか難しいものです。たとえば，先ほどだした例で「出生順と性格にはほとんど関係がない」といったときに，「でも私と姉は……」という話が出てしまうのは，「違いがあることと法則があることとは違う」ということも意味しているからです。

きょうだいであればそれぞれ，共通点がありつつ違うのは当たり前です。「違う」のは当然なのです。でもそのことと「一定の法則」つまり「長子ほどこう」とか「次子ほどこう」とか，そういう法則についてはなかなか断言することはできませんよ，ということを区別することが難しいのだ，ということなのです。

「きょうだいは違っている」のですが「そこに法則はほとんどない」のです。

過去記事との関連

今回の話は，前回の話にも通じる内容です。

そして以前，宝くじの記事を書きましたが，今回の話とその記事の内容も共通しています。そちらもどうぞ。