
宮沢賢治の宇宙(85) 「白鳥の停車場」はどこにあるのだろう?
「夏の大三角」と天の川
夏になると七夕伝説を思い出す。中国の伝説だ。愛し合う織女(しょくじょ、織り姫)と牽牛(けんぎゅう、彦星)は仲を割かれ、天の川を挟んで暮らすようになった。しかし、7月7日の夜だけ、天の川にカササギが橋をかけてくれるので年に一回の逢瀬ができる。子供の頃、七夕の夜は晴れて、二人が逢えることを願ったものだ。
織り姫星は「こと座」のヴェガ、彦星は「わし座」のアルタイルだ。夏の夜、夜空を眺めるとたしかに二つの星は天の川の対岸に見えている(図1)。

ヴェガとアルタイルは天の川を挟んで、かなり離れた位置にある。実際、どのぐらい離れているのだろうか?
まず、二つの星までの距離だが、ヴェガは25.04光年、アルタイルは16.73光年である。この段階で、二つの星までの距離には8.31光年の差がある。しかし、実際にはもっと離れている。見かけの方向が異なっているからだ。気になるので計算してみたら、8.78光年になった(付録参照)。
七夕の夜、織姫と彦星は逢えるのか?
ヴェガとアルタイルは約9光年も離れていたのだ。お互いの姿を目で見て確認したとしても、それぞれ約9年前の姿だ。光の速度が無限大ではなく、秒速30万キロメートルという有限な値なので、遠くのものを見ると、常に昔の姿しか見ることができないのだ。
また、光の速度で移動できるロケットがあったとしても、二人が出会うためには約9年の歳月がかかる。七夕の一夜では無理だ。ちなみに、時速約300キロメートルの東北新幹線を利用すると、324億年かかる。もうこれは絶望的な数字だ。現在の宇宙年齢は、まだ138億歳でしかない。
七夕伝説は、まさに伝説だったのだ。子供のときに、このことを知らなくてよかった。
銀河鉄道の駅はどこにあるのか?
織り姫星と彦星のデートは大変であることがわかった。ここでもう一度、図1をご覧いただきたい。着目して欲しいのは「はくちょう座」のデネブまでの距離だ。なんと、1400光年もある。織り姫星と彦星も遠くにあるが、たかだか20光年ぐらいだ。それに比べると圧倒的に遠くにある。
宮沢賢治の童話『銀河鉄道の夜』では、銀河ステーションを出た銀河鉄道はまず「白鳥の停車場」に停まる(図2)。この「白鳥の停車場」はいったい、どこにあるのだろう。

銀河鉄道の旅路については、以下のnoteを参照。
そして、もうひとつの駅。サウザンクロス駅はどこにあるのだろう?
「白鳥の停車場」はどこにあるのか?
ジョバンニを乗せた銀河鉄道は、銀河ステーションを出たあと、「白鳥の停車場」に到着する。この停車場はどこにあると思えばよいのだろう。一番目立つ星のそばに停車場を作るとすれば、「はくちょう座」のα星(一番明るい星)デネブのそばになる。
デネブまでの距離は1400光年。気が遠くなるほど遠い。
デネブのそばに停車場をつくれば、「はくちょう座」を堪能できるのだろうか? そう願いたいところだが、ダメだ。なぜなら、「はくちょう座」の北十字を作る星までの距離を調べてみると、バラバラなのだ(図3)。デネブの側だけなら大丈夫だが、「はくちょう座」の他の星まで遊びに行くのは、できそうもない。

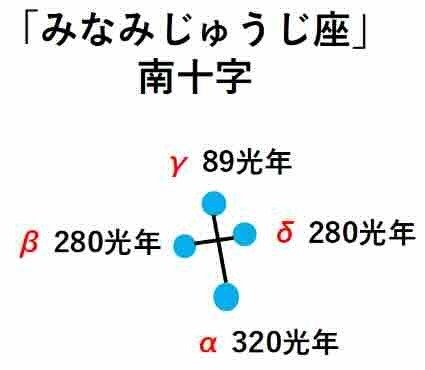
サウザンクロス駅はどこにあるのか?
じゃあ、サウザンクロス駅はどうだろう? 「みなみじゅうじ座」の南十字を形作る四つの星の距離を調べてみる(図4)。「はくちょう座」よりはマシだが、やはり距離に差がある。α星のそばにサウザンクロス駅を作ったとすれば、楽しめるのはやはりα星のそばだけになる。
『夜明けの停車場』
さて、困った。停車場を作る土地はたくさんありそうだが、どこに作っても他からは孤立した停車場になる。不便、極まりない。利用する人はほとんどいないだろう。それは、ジョバンニにとって、都合がよかったのだろうか? 人知れず、旅ができることは間違いない。
そんなことを考えていたら、昔の歌をひとつ思い出した。『夜明けの停車場』という歌だ。石橋正次の歌で、1972年リリース。
🎵 ひとりで旅に出る 俺は悪い奴(やつ) 🎵
ジョバンニよ、銀河鉄道の停車場の場所を教えておくれ。
付録 ヴェガとアルタイルの距離を計算してみる
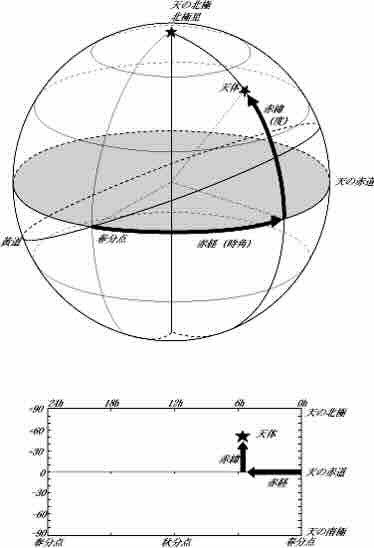
天体の方向を決める赤道座標系
天体の位置は天球に設定された座標系を用いて指定される。標準的に用いられる座標系は赤道座標系である(図5)。地球の自転軸が真北に向かう方向を“天の北極”とし、地球の赤道面を天球に投影したものを“天の赤道”とする。天の赤道面から天の北極方向に向かう角度を“赤緯”(赤道座標系における緯度)、そして、赤道面に沿う角度は“赤経” (赤道座標系における経度)と呼ぶ。赤経の原点は春分点であり、東回りで測っていくルールになっている。春分点は黄道(太陽が天球を通過する経路)と天の赤道が南から北へ交わる点のことである。
この赤道座標系を使うと、ヴェガとアルタイルの方向は次のように表わせる。
ヴェガ (赤経、赤緯)=(18時36分56秒, +36° 47′ 01″)
アルタイル (赤経、赤緯)=(19時50分47秒, +08° 52′ 06″)
赤経は時分秒で表される。赤道面を一周すると、360°なので、1時間は15°に相当する。一方、赤緯は角度で表される。角度の分(分角)「′」は1/60°、角度の秒(秒角)「″」は1/60′=1/3600°である。単位が二種類あると面倒なので、度(°)に統一すると、二つの星の方向は次のようになる。
ヴェガ (赤経、赤緯)= (279.2°, +36.8°)
アルタイル (赤経、赤緯)= (297.7°, +08.9°)
三次元情報が必要なので球面座標系を使う
星の見える方向を指定することができた。これに、星までの距離を加えると、3次元空間における位置がわかる。
r:星までの距離
θ, φ:星の見える方向(赤経、赤緯)
これら三つの変数(r, θ, φ)で表す座標系は球面座標系と呼ばれる。
普通の三次元座標系(デカルト座標系)における点の位置 :(x, y, z)
球面座標系における三つの変数 :(r, θ, φ)
これらには以下の関係がある。
x = r sinθ cosφ
y = r sinθ sinφ
z = r cosθ
二つの星の位置は球面座標系では次のようになる。
ヴェガ (r, θ, φ)= (25.04光年, 53.2°, 279.2°)
アルタイル (r, θ, φ)= (16.73光年, 81.9°, 297.7°)
ここで、角度の定義上、次の関係がある。
θ=90°— 赤緯
また、ここで必要なのは相対位置なので、φの値から一律に270°差し引くと、次を得る。
ヴェガ (r, θ, φ)= (25.04光年, 53.2°, 9.2°)
アルタイル (r, θ, φ)= (16.73光年, 81.9°, 27.7°)
最後はやはり普通の三次元座標系
これらの値を使うと、二つの星の位置 (x, y, z) は次のようになる。
ヴェガ (xV, yV, zV)=(19.79光年, 20.21光年, 15.00光年)
アルタイル (xA, yA, zA)=(16.63光年, 7.68光年, 2.36光年)
ここで添え字の V と Aはヴェガとアルタイルを表す。これらの添字は本来は下付きの添え字だが (x_V など)、noteのツールの都合上、xVになっている。ご了承ください。
これで馴染みのある三次元座標系(デカルト座標系)になった。では、二つの星の距離dを計算しよう。
d = √(xV — xA)2+(yV — yA)2+(zV — zA)2
= √9.99+58.98+8.12
= 8.78 光年
これが答えだ。
