モノづくりの業務効率化に貢献するITのお仕事（CAE）について -5-

CAE（Computer Aided Engineering）に関する記事の5回目です。私の生業（本業）でもあります。

前回はコラムとして「マルチフィジックス解析」について話をしました。マルチフィジックス解析を通じて、高精度な物理現象の予測が可能になります。

今回はまた別のコラムとして「マルチスケール解析」について話をします。マルチスケール解析とは、文字通りスケールの異なる解析対象の双方の物性、もしくは挙動を連成させる解析を意味します。

有限要素法とは異なる解析手法も出てくるので、そこが面白い部分であると感じています。

マルチスケール解析の背景

近年は多くの製品に複合材料が利用されています。複合材料とは基礎となる母材に強化繊維などの分散材を組み合わせることにより、母材本来の特性に靱性や耐熱性などの機能を追加したものです。

FRP（Fiber Reinforced Plastics）と呼ばれる繊維強化プラスチックが実用例としてあります。母材にプラスチックを用いて軽量化や高い成形性を持たせ、ガラス繊維で高強度化を実現させた複合材料です。

FRPの中でも、特に軽量化や高強度化を実現させたのが炭素繊維強化プラスチック（CFRP）です。

CFRP（Carbon Fiber Reinforced Plastics）は炭素繊維（カーボンファイバー）で強化されたプラスチックの略称です。自動車や航空機などの構造部品に使用されています。

このように繊維部分というミクロ構造をもつ材料は、通常の有限要素法では十分な精度を出すのが難しいとされています。ミクロ構造の力学特性を正しく考慮することが困難であるためです。

マルチスケール解析の手法 -1-

マルチスケール解析と書いても様々なアプローチがあります。代表的な手法としては、均質化法が幅広く知られています。

例えば、先ほど紹介した複合材料などは複数の異種材料から成り立つため、仮にこの複合材料の材料特性を均質な形に変換できれば、製品全体の挙動を把握することができます。

特にFRPやCFRPでは、母材に対して繊維部分がミクロ構造に相当します。このミクロ構造とマクロ等価物性の関係に関する理論が均質化法です。

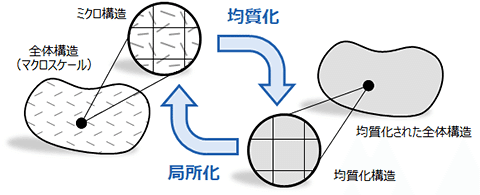
ミクロ構造から等価物性を計算する均質化と、均質化された材料の物理量からミクロ構造の状態（応力分布）を計算する局所化に分けられます。

汎用的な構造に対して均質化を適用する手法も開発されました。有限要素法で支配方程式を離散化しますが、ミクロ構造は要素分割（メッシュ）で表現し、材料特性は有限要素法の材料モデルとして表現します。

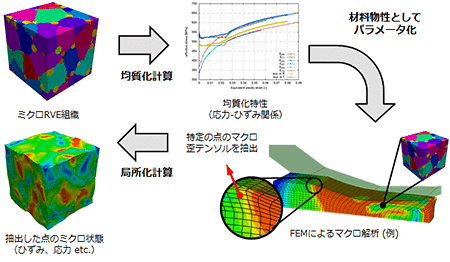
近年ではマクロ構造の材料特性をより理論的に紐解くために、ミクロ構造の現象自体にも注目が集められています。ミクロとマクロの橋渡しをする均質化法が存在感を発揮しているのです。

出典：均質化法がつなげるマルチスケールの世界
https://www.engineering-eye.com/rpt/column/2018/0413_structural-1.html

マルチスケール解析の手法 -2-

もうひとつのアプローチとして、分子レベルの挙動を求める解析手法「分子動力学法」を用いて材料特性を詳細に把握して、そこから有限要素法に持ち込むことも行われています。

分子動力学法（MD：Molecular Dynamics）とは、原子を質点として運動方程式を導出（離散化）して、それを連立方程式の要領で解くことで、個々の原子の物理量を求めます。

原子間の相互作用（原子間ポテンシャル）から個々の原子に対する運動方程式を立てる方法、個々の原子の種類と電子数のみを入力パラメータにして量子力学に基づいて運動を求める方法（第一原理計算）があります。

この手法は先ほどの均質化法よりも物理的な原理を重視したもので、マクロの材料特性を詳細化するための代表的なアプローチです。計算時間はかかりますが、より確実性を追求しています。

マルチスケール解析の重要性

物質の密度やエネルギーなどのマクロの材料特性は、そもそも原子単位の配置や運動などのミクロ構造の挙動から決まります。有限要素法はマクロ構造の特性に基づいた解析（シミュレーション）と言えます。

これは「マクロの特性が分かれば十分な解析精度が得られる」ということを前提としています。基本的にミクロ構造を有さない、もしくは大して存在しない場合は、通常の有限要素法でも事足ります。

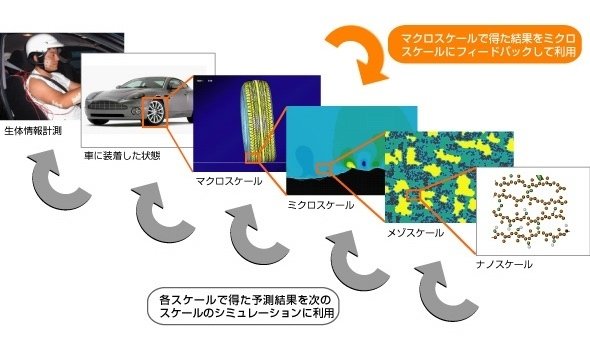
ただし、近年は複合材料の強い存在感もあり、材料自体の素過程をきちんとモデル化することが重要視されています。コンピューターの計算能力も向上してきているので、それも追い風になっています。

前回のマルチフィジックス解析と同様に、マルチスケール解析もまたひとつの要求水準として、CAEベンダーに求められる課題でもあるのです。

おわりに

今回は「マルチスケール解析」の話をしました。前回のマルチフィジックス解析と同じく難易度の高い技術ではありますが、より高精度な解析（シミュレーション）を実現できます。

実はマルチスケール解析はノーベル化学賞を2013年に受賞しています。タイトルは「複雑な化学反応系のマルチスケールモデルの開発」であり、たんぱく質の構造のコアは量子力学で計算し、その周りは古典力学で計算するというものです。

古典力学と量子力学の連携が革新的であると評価されました。CAEとして新たなアプローチが認められた瞬間です。なかなか面白い研究だと思います。

今回でCAEに関する話は終わりになりますが、また機会があれば別の切り口で書こうと思いますので、引き続きよろしくお願いします。

-------------------------
最後まで読んで頂き、ありがとうございます。この記事があなたの人生の新たな気づきになれたら幸いです。今後とも宜しくお願いいたします♪♪
-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎