力学の基本解説〜質点と剛体と連続体について〜

2021年3月16日 08:03

今回は理系の記事。力学と言うと難しくて堅苦しい表現になるが、物体の運動の基本である、質点と剛体と連続体について解説をしてみた。

主に大学生向けの範囲になるので、難解なところもあるかもしれないが、できる限り分かりやすく書いていこうと思う。

物体の扱い方について

ある物体が力を受けて、運動を始める。その過程について考える学問を「力学」と言う。学問的に表現するならば「物質の運動およびその運動をひきおこす力を研究するもの」である。

力学の世界では、物体の扱い方について、次の３種類に分類している。

（１）質量だけを持つ仮想的な物体＝【質点】
（２）質量と大きさ（形状）を持つ物体＝【剛体】
（３）質量が連続的に分布する物体＝【連続体】

質点は物体を最も簡単にしたもので、手計算でも十分に扱える。また、剛体も質点に物体の形状を加味しただけなので、ギリギリだが手計算で問題ない。問題は連続体で、情報量が膨大になるため、コンピューターで計算することで対応するのが一般的である。

おそらく、高校の物理で扱うのは（１）の「質点」までだろう。他のふたつは大学で学習する範囲である（自分は高専に居たので、高校のカリキュラムは把握していないのだが）。

運動に関しては、直線運動や回転運動などいくつかの形態があることは、何となくイメージできると思う。ここでの問題は、何を見て直線運動か回転運動かを判断するのかということ。

結論から言うと、次の３つの情報（扱う範囲）によって決まる。

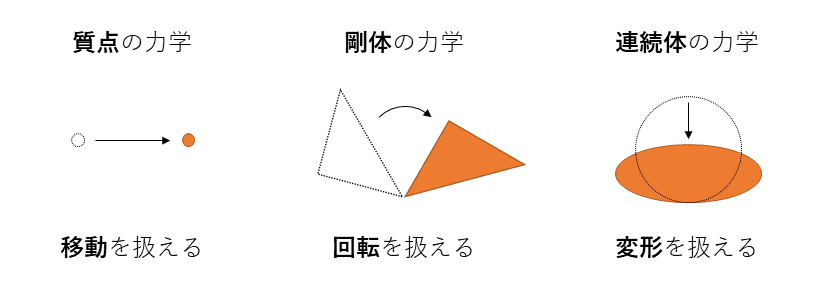
（１）物体の位置の変化＝【直線】
（２）物体の姿勢の変化＝【回転】
（３）物体の形状の変化＝【変形】

上の図にあるように、質点は直線運動のみ扱うことができ、剛体は直線運動と回転運動を扱うことができる。連続体はこれらに加えて変形を扱う。

質点はその名の通り点なので、あくまで仮想的な物体と言える。イメージとしては、物体の質量を凝縮させたビー玉のような感覚である。

剛体は大きさを考慮するので、回転する円盤や振り子をイメージするとちょうど良い（厳密に言えばこれらも連続体だが、変形はほとんど無視できるので剛体とみなしている）。

連続体は至る所の変形を扱う。変形に対する理論計算の式はあるが、それらは厳密で複雑である。そのため、先程書いたように、コンピューターに計算の処理を任せる必要がある。

私の仕事（CAE：Computer Aided Engineering）の話になるが、私たちはコンピューターシミュレーションの中で現実の物体を対象とするので、基本的に問題を連続体として扱う。ただ、問題を簡略化したい場合に、質点や剛体で事象を再表現することもある。

例えば、問題を簡略化して手計算で出した答えと、シミュレーションで出した答えを比較することで、計算の妥当性を検証するような場合である。

今回は力学の基本となる運動の捉え方について、質点と剛体と連続体を紹介しながら解説してみた。先に書いた通り、基本的に大学で習う範囲のことなので、その辺の方々に役立てられたら幸いである。

-------------------------

最後まで読んでいただき、ありがとうございました。マイペースでほぼ毎日の更新に取り組んでいます。何卒よろしくお願いいたします。

-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ブログのロードマップ ⭐︎⭐︎⭐︎