
変位・速度・加速度と微分・積分の関係を解説する
質点の力学の話。おそらく、大学(理系)の最初に習うことだと思う。私は高専出身ゆえに実態が掴めていないので、間違えてたら申し訳ない。
高校物理では「等加速度直線運動」の単元が一番近いのだが、ほとんどが「公式を覚えるのに苦労した」という印象ではないだろうか。そのうちのひとつを下に書いたのだが、係数が分数であるなど、結構な曲者である。

(※)この画像(数式)は次のページから拝借した。
私はただひたすら公式を覚えるのが苦手で、学習した当時は「背景」を説明してほしいと何度も思った。
ただ、その背景にあるのは、これまた理解の難しい「微分・積分」の話なので、高校物理で説明するのはかなり無理がある。
今回は力学の基礎である「変位・速度・加速度」について、微分・積分を利用して解説する。
(※)変位は質点の位置の変化(移動量)である。
変位・速度・加速度をグラフで説明する:等速直線運動
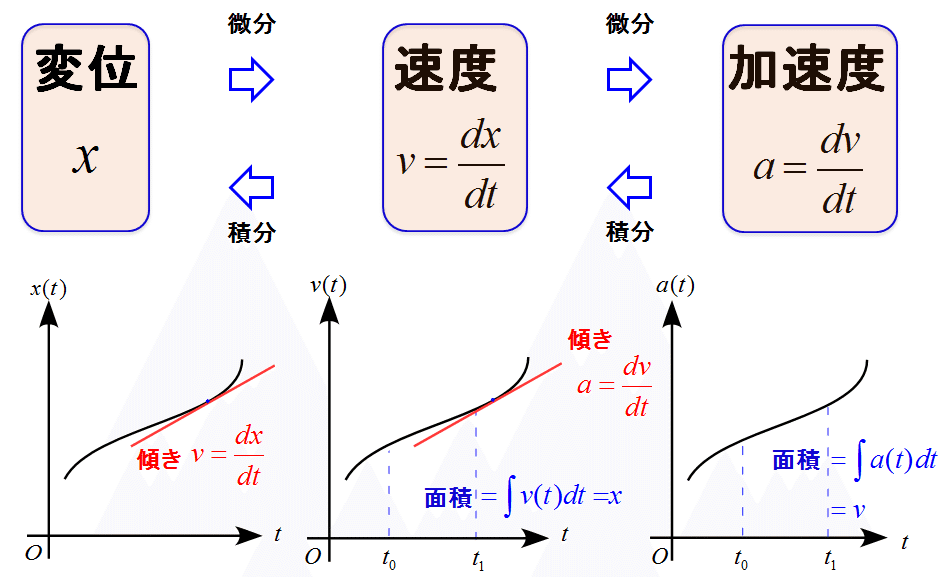
公式と言うより、原理原則に近い話なので、まずはこの原理原則を受け止めてほしい。すなわち、次のようなことである。
変位を1階微分したのが速度であり、速度を1階微分したのが加速度である。つまり、変位を2階微分したのが加速度である。
そもそも微分とは、グラフで言うところの「ある位置における接線(傾き)」である。横軸に時間(t)を取るならば、単位時間当たりの変化量である。
つまり、グラフの縦軸を変位とするならば、このグラフの傾き(微分)は速度である。また、縦軸を速度とするならば、グラフの傾き(微分)は加速度である。
例えば、次のグラフは「等速直線運動」における時間と変位の関係である(変位の初期値はゼロである)。
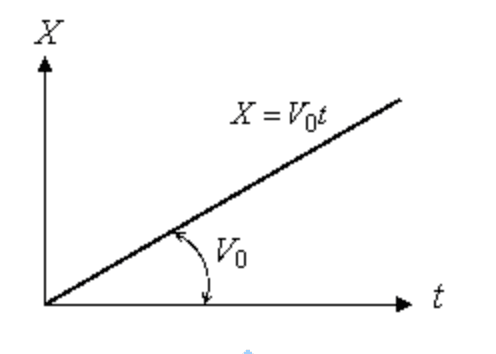
変位は原点を通る時刻(t)の1次関数であり、傾きは初速度(一定値)であることが理解できるだろう。
また、縦軸を速度とするならば、速度は初速度で一定値であるため、加速度(傾き)はゼロである。
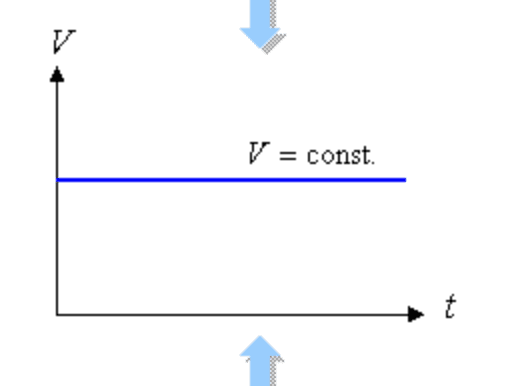
速度を1階積分、もしくは加速度を2階積分すると変位となる。また、ここでは積分は「ある区間におけるグラフの面積」という意味を持つ。
等速直線運動の場合、時刻と速度のグラフで時刻(積分区間)と初速度(定数)を掛け算すれば、おのずと面積が求まる。つまり、変位のグラフは時刻(t)の1次関数であり、先ほどの話とも一致する。
変位・速度・加速度をグラフで説明する:等加速度直線運動

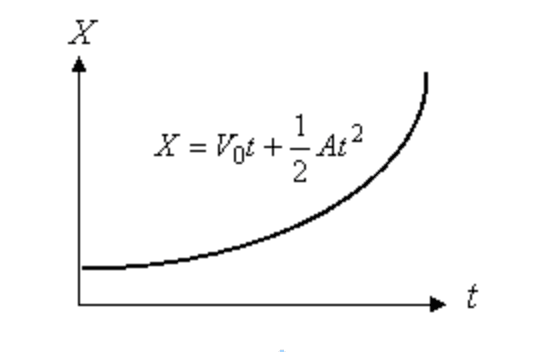
次に本題の「等加速度直線運動」について話をする。今度は加速度が定数で、速度は時刻(t)の1次関数となる。次のグラフの通りである。なお、今回は初速度の値も加味している。
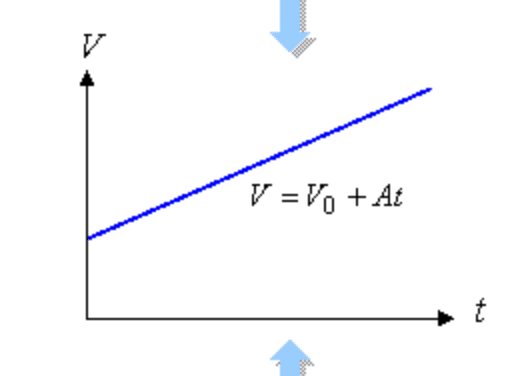
ここから変位を求めるわけだが、積分とは「ある区間におけるグラフの面積」である。時刻(積分区間)を指定すれば、台形の面積の公式が使えて、最初に示した数式の通りになる。
もしくは、速度の式から積分の公式を適用すると、同じく最初に示した式にたどり着くはずである(初期変位はゼロとしているので、積分定数が出てきてもゼロとしてキャンセルされる)。
速度の式の2項目は時刻(t)の1次関数なので、ここを積分すると、係数に分数の値が出てくることも理解できるだろう。
おわりに
今回は微分・積分の考え方を利用して、質点の力学(変位・速度・加速度)の公式を導出してみた。
何事もそうだが、公式の背景を知ることで、より理解度が増す。今回で皆さんの理解度を深められたかどうかはわからないが、必要な人にとっての復習教材として利用されることを願いたい。
-------------------------
最後まで読んでいただき、ありがとうございました。ゆるりとほぼ毎日の更新で取り組んでいます。気まぐれ感はありますが、何卒よろしくお願いいたします。
-------------------------
⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎
⭐︎⭐︎⭐︎ ブログのロードマップ ⭐︎⭐︎⭐︎
この記事が気に入ったらサポートをしてみませんか?
