メービウス変換が織りなすシュタイナー円周族

2024年10月20日 16:20

Inversion theory and conformal mapping David E.Blair AMS

半径$${r}$$の円$${C}$$の外点$${P^{'}}$$から$${C}$$へ接線を引き、接点$${T}$$ から直線$${OP{'}}$$に垂線を落としその足を$${P}$$とする。
△$${OPT}$$と△$${OPT^{'}}$$は直角３角形で互いに相似になっている。 OPの長さｘOP'の長さ＝$${r^2}$$である。
このときPとP'はCに関して対称（inverse反転)であると言われる。
また、円$${C}$$は$${P}$$と$${P^{'}}$$を極限値とするアポロニウスの円として知られている。実際、$${P,P'}$$ のかわりに複素数$${z_1,\,\,z_2}$$、円$${C}$$上の点を$${z}$$で表すと $${\left| z-{{z}_{1}} \right|\left| z-{{{z}_{2}}} \right|={{r}^{2}}}$$ となる。

上は、$${w=1/z}$$ の図である。すなわち、$${z=x+iy}$$,$${w=u+iv}$$と置くとき、$${(x,y)}$$ を左のX,Y座標に、$${(u,v)}$$を右のU,V座標に置く。このとき、$${x+iy=\frac{1}{u+iy}=\frac{u-vi}{{{u}^{2}}+{{v}^{2}}}}$$
より$${z}$$平面上の直線$${x=c}$$ および$${y=d}$$はそれぞれ$${w}$$ 平面上の円
$${{{\left( u-\frac{1}{2c} \right)}^{2}}+{{v}^{2}}=\frac{1}{4{{c}^{2}}}}$$ ,
$${{{u}^{2}}+{{\left( v-\frac{1}{2d} \right)}^{2}}=\frac{1}{4{{d}^{2}}}}$$
に写像される。$${c,d}$$ をいろいろ変化させると、$${z}$$平面上に碁盤の目の格子ができるが、それが$${w=\frac{1}{z}}$$ という写像により、$${w}$$ 平面上原点に接点をもつ円で、縦方向に大きくなる円周族Aと、横方向に大きくなっていく円周族Bがつくる模様ができる。この時注意することは、直線$${x=c}$$と直線$${y=d}$$が直交しているにしたがって、円周族Aと円周族Bは直交している。この場合円と円が直交するというのは、2つの円の接点でそれぞれ接線をひいたときに、２つの接線の間の角度が90°であることである。これは
$${\frac{dw}{dz}=-\frac{1}{{{z}^{2}}}\ne 0}$$
による等角性がその理由である。一般にメービウス変換
$${w=\frac{az+b}{cz+d}}$$,$${ab-cd\ne 0}$$
に対して、等角性$${\frac{dw}{dz}=\frac{ad-bc}{{{\left( cz+d \right)}^{2}}}\ne 0}$$が面白い幾何学を作り出す。メービウス変換は円円変換をもたらすことが知られている。ただしこの場合直線は無限遠点を通る円として直線も円と考えていることに注意しよう。そして上に述べた対称点を保存する。つまり、$${P,P'}$$ のかわりに複素数$${{{z}_{1}},{{z}_{2}}}$$ を円$${C}$$ に関する対称点とするとメービウス変換$${w=T\left( z \right)}$$によって円$${C}$$は円$${T\left( C \right)}$$にうつり、$${{{w}_{2}}=T\left( {{z}_{2}} \right)}$$は円$${T\left( C \right)}$$に関して$${{{w}_{1}}=T\left( {{z}_{1}} \right)}$$の対称点になる。このとき$${\frac{\left| z-{{z}_{1}} \right|}{\left| z-{{z}_{2}} \right|}=\rho }$$ と書ける。ここで、$${\rho }$$は正の定数。このとき、$${\rho =1}$$ のときは、$${z}$$は$${{{z}_{1}}}$$ と$${{{z}_{2}}}$$ から等距離の位置にありアポロニウスの円は$${{{z}_{1}}}$$と$${{{z}_{2}}}$$の中点をとおる２等分線という直線になる。また$${\rho \ne 1}$$ のとき、$${\rho >1}$$か$${\rho <1}$$ に従って、２等分線の左側、あるいは右側にアポロニウスの円ができる。

$${w=\frac{az+b}{cz+d}=T\left( z \right)}$$の２点$${z=0}$$ と$${z=\infty }$$ を通る$${z}$$ 平面の円周族（実は原点を通る放射状に延びる直線族）$${A}$$ は、$${T\left( 0 \right)=\frac{b}{d}=p}$$ と$${T\left( \infty \right)=\frac{a}{c}=q}$$を通る$${w}$$ 平面の円周族Bに写像される。$${z}$$平面の原点を中心とする同心円の円周族$${A'}$$の写像である円周族$${B'}$$は$${B}$$ に直交する。これは等角性の帰結である。ゆえに２点$${p,q}$$ を通る円周族$${B}$$（第１種）と直交する円周族$${B'}$$（第２種）の２種類の存在がわかる。$${B}$$に属する特殊の２円すなわち、直線$${p,q}$$と線分$${pq}$$を直径とする円に着目すれば、両者に直交する円周族$${B'}$$の円は直線$${p,q}$$上に中心を有し線分を調和に保つことが言われる。かかる場合$${p,q}$$ ２点はこの円に関して対称である。ここで、記号を変えるが点列が調和であることの定義をしておく。

ｚ_1 とz_2を極限値とする第１種のシュタイナーの円（Nevalinna,Rolf;Paatero,Veikko　Introduction to complex analysis p.41)

$${C}$$ を極限点$${{{z}_{1}},{{z}_{2}}}$$ とする第１種のシュタイナーの円（これはあとから説明するがアポロニウスの円のこと）とする。$${{{z}_{1}},{{z}_{2}}}$$ をとおる直線が$${C}$$を切って２つの反対側にある$${z=a}$$ と$${z=b}$$ に分かつ。このとき、$${C}$$ の定義より非調和比$${\left( a,b,{{z}_{1}},{{z}_{2}} \right)=\frac{\left( a-{{z}_{1}} \right)/\left( a-{{z}_{2}} \right)}{\left( b-{{z}_{1}} \right)/\left( b-{{z}_{2}} \right)}=-1}$$がなりたつ。$${\left( a,b,{{z}_{1}},{{z}_{2}} \right)=-1}$$が成り立つとき、列$${a,b,{{z}_{1}},{{z}_{2}}}$$は調和であるといわれる。そして、メービウス変換$${T}$$ が非調和比をかえないことから$${\left( Ta,Tb,T{{z}_{1}},T{{z}_{2}} \right)=-1}$$となり$${{{w}_{1}}=T{{z}_{1}}}$$,$${{{w}_{2}}=T{{z}_{2}}}$$ において、$${{{z}_{1}},{{z}_{2}}}$$ が円$${C}$$ に関して対称であることから$${{{w}_{1,}}{{w}_{2}}}$$ が円$${T\left( C \right)}$$ に関して対称となる。(幾何学に詳しい人にはこれで十分だが、後でこのことを式を用いた別証明を与える）。

circle inversion 反転についてのビデオ

シュタイナーの円周族（Steiner cicles)はいくつかの書物に登場する。代表的なものを２つ

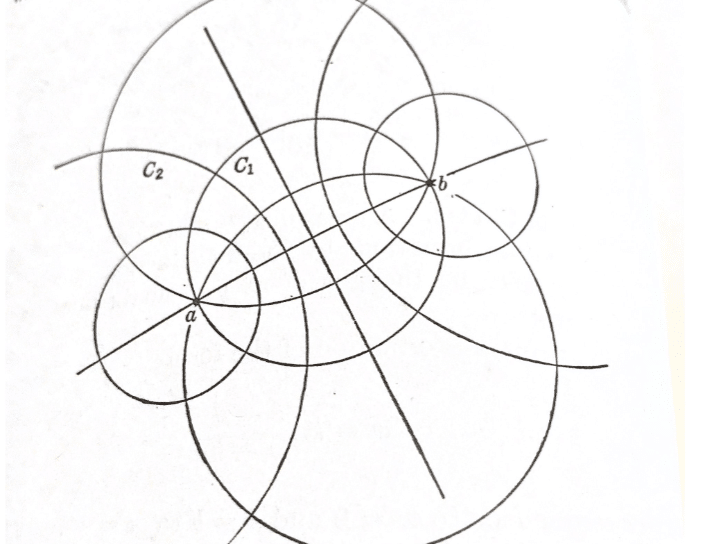
この図では$${a,b}$$ をとおる円を$${C_1}$$,$${a,b}$$ を極限点とするアポロニウスの円を$${C_2}$$となっている。

R.Courant Theory of a complex variable,p.39

我々は、極限点$${{{z}_{1}},{{z}_{2}}}$$に属するシュタイナー円周族のすべてを構成できる。$${\frac{\left| z-{{z}_{1}} \right|}{\left| z-{{z}_{2}} \right|}=\rho }$$における$${\rho}$$ を変えることによりさまざまなアポロニウスの円ができるが、これを第１種のシュタイナーの円周族と呼ぶ、$${{{z}_{1}},{{z}_{2}}}$$をとおる円たちからなるものは第２種のシュタイナーの円周族である。第１種と第２種の円周族はたがいに直交している。

円$${C}$$ に関して、2点が対称であるということを上では点列が調和と言うことで定義したがそれと同等の条件（必要十分）である次の形で定義される事が多い。

円$${C}$$ :$${\left| z-{{z}_{0}} \right|=r}$$ に関して、2点$${{{z}_{1}},{{z}_{2}}}$$ が対称（あるいは反転）になっているというのは、
$${\arg \left( {{z}_{1}}-{{z}_{0}} \right)=\arg \left( {{z}_{2}}-{{z}_{0}} \right)}$$
かつ
$${\left| {{z}_{1}}-{{z}_{0}} \right|\left| {{z}_{2}}-{{z}_{0}} \right|={{r}^{2}}}$$
を満足することをいう。（冒頭の$${P}$$と$${P^{'}}$$およびアポロニウスの円参照）したがって、円$${C}$$ :$${\left| z-{{z}_{0}} \right|=r}$$ に関してたがいに対称になっている２点$${{{z}_{1}},{{z}_{2}}}$$は
$${{{z}_{1}}={{z}_{0}}+l\varepsilon }$$ , $${{{z}_{2}}={{z}_{0}}+\frac{{{r}^{2}}}{l}\varepsilon }$$（$${\varepsilon ={{e}^{i\varphi }}}$$）
の形に表される。円$${C}$$上の一点を$${z={{z}_{0}}+r\eta ,\,\,\eta ={{e}^{i\theta }}}$$とすれば、
$${\left| \frac{z-{{z}_{1}}}{z-{{z}_{2}}} \right|=\left| \frac{r\eta -l\varepsilon }{r\eta -\frac{{{r}^{2}}\varepsilon }{l}} \right|}$$ $${=\frac{l}{r}\left| \frac{r\eta -l\varepsilon }{l\eta -r\varepsilon } \right|=\frac{l}{r}\left| \frac{r\eta -l\varepsilon }{l\bar{\eta }-r\bar{\varepsilon }} \right|=\frac{l}{r}}$$
となる。逆に$${\left| \frac{z-{{z}_{1}}}{z-{{z}_{2}}} \right|=\rho }$$, $${\rho \ne 1}$$ は2点$${{{z}_{1}},{{z}_{2}}}$$が対称となるような円を表す。そのことを示そう。
$${\left| \frac{z-{{z}_{1}}}{z-{{z}_{2}}} \right|=\rho }$$はつぎのように書き直される。
$${{{\left| z \right|}^{2}}-2\Re \left( {{{\bar{z}}}_{1}}z \right)+{{\left| {{z}_{1}} \right|}^{2}}={{\rho }^{2}}\left[ {{\left| z \right|}^{2}}-2\Re \left( {{{\bar{z}}}_{2}}z \right)+{{\left| {{z}_{2}} \right|}^{2}} \right]}$$
$${{{\left| z \right|}^{2}}-2\frac{\Re \left[ \left( {{{\bar{z}}}_{1}}-{{\rho }^{2}}{{{\bar{z}}}_{2}} \right)z \right]}{1-{{\rho }^{2}}}+\frac{{{\left| {{z}_{1}} \right|}^{2}}-{{\rho }^{2}}{{\left| {{z}_{2}} \right|}^{2}}}{1-{{\rho }^{2}}}=0}$$
$${{{\left| z-\frac{{{z}_{1}}-{{\rho }^{2}}{{z}_{2}}}{1-{{\rho }^{2}}} \right|}^{2}}=\frac{{{\left| {{z}_{1}}-{{\rho }^{2}}{{z}_{2}} \right|}^{2}}}{{{\left( 1-{{\rho }^{2}} \right)}^{2}}}-\frac{{{\left| {{z}_{1}} \right|}^{2}}-{{\rho }^{2}}{{\left| {{z}_{2}} \right|}^{2}}}{1-{{\rho }^{2}}}}$$
ここで、
$${{{\left| {{z}_{1}}-{{\rho }^{2}}{{z}_{2}} \right|}^{2}}-\left( 1-{{\rho }^{2}} \right)\left( {{\left| {{z}_{1}} \right|}^{2}}-{{\rho }^{2}}{{\left| {{z}_{2}} \right|}^{2}} \right)={{\rho }^{2}}{{\left| {{z}_{1}}-{{z}_{2}} \right|}^{2}}}$$
であることを使えば、
$${\left| z-\frac{{{z}_{1}}-{{\rho }^{2}}{{z}_{2}}}{1-{{\rho }^{2}}} \right|=\frac{\rho \left| {{z}_{1}}-{{z}_{2}} \right|}{\left| 1-{{\rho }^{2}} \right|}}$$
となる。この方程式は中心　$${{{z}_{0}}=\frac{{{z}_{1}}-{{\rho }^{2}}{{z}_{2}}}{1-{{\rho }^{2}}}}$$、半径$${r=\frac{\rho \left| {{z}_{1}}-{{z}_{2}} \right|}{\left| 1-{{\rho }^{2}} \right|}}$$なる円をあらわし
$${{{z}_{1}}-{{z}_{0}}=\frac{{{\rho }^{2}}\left( {{z}_{2}}-{{z}_{1}} \right)}{1-{{\rho }^{2}}}}$$ , $${{{z}_{2}}-{{z}_{0}}=\frac{{{z}_{2}}-{{z}_{1}}}{1-{{\rho }^{2}}}}$$
であるから、定義とてらしあわせれば$${{{z}_{1}}}$$ と$${{{z}_{2}}}$$はたがいにこの円に関して対称な２点である。また、$${\rho =1}$$ の場合には、$${\left| \frac{z-{{z}_{1}}}{z-{{z}_{2}}} \right|=\rho }$$は2点$${{{z}_{1}},{{z}_{2}}}$$の垂直2等分線になっている。

つぎに、円$${\left| \frac{z-{{z}_{1}}}{z-{{z}_{2}}} \right|=\rho }$$に関して対称な２点$${{{z}_{1}},{{z}_{2}}}$$は$${T(z)=\frac{az+b}{cz+d}}$$の結果、対称な２点$${T({{z}_{1}}),T({{z}_{2}})}$$にうつる。実際$${w=\frac{az+b}{cz+d}}$$から$${z=\frac{-dw+b}{cw-a}}$$として、これを代入すると
$${\left| \frac{dw-b-{{z}_{1}}\left( -cw+a \right)}{dw-b-{{z}_{2}}\left( -cw+a \right)} \right|=\rho }$$
$${\left| \frac{w-\frac{a{{z}_{1}}+b}{c{{z}_{1}}+d}}{w-\frac{a{{z}_{2}}+b}{c{{z}_{2}}+d}} \right|=\rho \left| \frac{c{{z}_{1}}+d}{c{{z}_{2}}+d} \right|}$$
$${\left| \frac{w-T\left( {{z}_{1}} \right)}{w-T\left( {{z}_{2}} \right)} \right|=\rho \left| \frac{c{{z}_{1}}+d}{c{{z}_{2}}+d} \right|}$$
よりわかる。

メービウス変換では不動点を考えて、メービウス変換の型分類がおこなわれる。その際、ｚ平面、ｗ平面というのを別々に考えるのではなく、ｚ平面とｗ平面を同じ座標で考える。
F.Klein は不動点$${{z}_1,{z}_2}$$をとおる円の族の行動を考察することでメービウス変換の構造を洞察できると考えた。

もう一つの函数論入門　谷口雅彦著　京都大学学術出版会において次の図を見ることができる