
自由エネルギー原理の解説:知覚・行動・他者の思考の推論 6
離散系モデルにおける自由エネルギー原理の実装
この文献では離散系モデル、特にマルコフ決定過程(MDP)の枠組みにおける自由エネルギー原理の実装について詳しく説明しています。
1. 離散系の生成モデル
連続系モデルとは異なり、離散系モデルでは、隠れ状態 xt と感覚入力 st は離散値を取ります。これは、例えば、ある時刻において、可能な状態や入力が有限個しかない状況を表現できます。
ソースによると、離散系の生成モデルは、以下の要素で構成されます。
●尤度行列 A: 隠れ状態 xt から感覚入力 st への変換確率を表します。
●遷移行列 Bπτ: 時刻 τ-1 の隠れ状態 xt-1 から時刻 τ の隠れ状態 xt への遷移確率を表します。行動方策 π によって変化します。
●初期状態の確率分布: 最初の隠れ状態 x1 の確率分布を表します。
これらの要素を用いて、離散系の生成モデルは以下のように表されます。

ここで、
●s̃ = (s1, s2, ..., sT): 長さ T の感覚入力のシークエンス
●x̃ = (x1, x2, ..., xT): 長さ T の隠れ状態のシークエンス
●π: 行動方策
●θ: パラメータのセット (A, B, D など)
●m: 生成モデルの構造
2. 変分自由エネルギーと推論
離散系モデルにおける変分自由エネルギーは、以下の式で表されます。

●xπτ: 行動方策 π のもとでの、時刻 τ における隠れ状態 xτ の事後確率の期待値
この変分自由エネルギーを最小化するように隠れ状態の事後確率を最適化することで、推論を行います。具体的には、F(π) を xπτ について変分し、その結果を 0 と置くことで、以下の更新式が得られます。
ここで、σ(⋅) はソフトマックス関数です。
3. 学習
学習は、変分自由エネルギーを最小化するパラメータ θ (A, B, D) を見つけるプロセスです。具体的には、F(π) を各パラメータについて変分し、その結果を 0 と置くことで、以下の更新式が得られます。

ここで、⊗ は外積を表します。これらの更新式は、ヘブ則に似た形をしており、感覚入力と隠れ状態の共起に基づいてパラメータが更新されることを示しています。
4. 行動方策の最適化
エージェントは、将来にわたって期待される自由エネルギー(expected free energy)を最小化するように行動方策 π を選択します。期待自由エネルギーは、以下のように定義されます。



行動方策の選択は、変分自由エネルギーと期待自由エネルギーの重み付き和を最小化するように行われます。
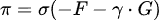
その他

それぞれの項の意味を説明します。
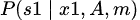
観測モデル: 最初の観測 s1s_1s1 が最初の状態 x1x_1x1 に依存してどのように生成されるかを示しています。ここで AAA は観測モデルのパラメータを表し、観測と状態の関係を規定します。観測 sss は状態 xxx に依存して生成されるため、これは観測確率を表すものです。

初期状態の分布: 最初の状態 x1x_1x1 が、データ DDD やモデル mmm に基づいてどのように決まるかを示す確率分布です。この初期状態は、事前にある程度の知識(データやモデル)が与えられている場合の状態の確率分布です。

後続の観測生成プロセス: 時刻 τ=2\tau = 2τ=2 から TTT までの観測 sτs_\tausτ が、各時刻の状態 xτx_\tauxτ に依存して生成されることを示しています。観測モデル AAA が引き続き使われ、観測と状態の間の関係を示します。これは状態に基づく観測確率の時間的な推移を表現しています。

状態遷移モデル: 時刻 τ=2\tau = 2τ=2 から TTT までの状態 xτx_\tauxτ が、前の時刻 τ−1\tau-1τ−1 の状態 xτ−1x_{\tau-1}xτ−1 に基づいてどのように遷移するかを示しています。ここで BπτB_\pi^\tauBπτ は、政策(行動選択) π\piπ に依存した遷移モデルのパラメータを表します。つまり、政策 π\piπ によって、状態の遷移がどのように制御されるかを示しています。これは、マルコフ過程(時間ステップごとの遷移)が行動によって影響を受けることを表現しています。

政策の事前分布: 政策 π\piπ が、モデル mmm に依存してどのように選択されるかを示しています。これは、行動選択の確率分布であり、どの行動が選択されるかをモデル化します。

パラメータの事前分布: パラメータ θ\thetaθ がモデル mmm に基づいてどのような値をとるかを示しています。これは、モデルのパラメータに関する事前の知識を表します。パラメータ θ\thetaθ は、観測モデルや状態遷移モデル、政策選択モデルなどに関与しており、これらのモデルに対する事前の信念を反映します。
全体の解釈
この式全体は、次の要素からなる生成モデルを表しています:
観測モデル: 各時刻の状態に基づいて観測がどのように生成されるか。
状態遷移モデル: 各時刻で、前の状態に基づいて次の状態がどのように遷移するか。
政策(行動)モデル: 行動選択 π\piπ に基づいて状態遷移がどのように影響を受けるか。
パラメータの事前分布: モデルのパラメータに関する事前知識。
この生成モデルは、ベイズ的推論の枠組みで使われ、観測データに基づいて未知の状態やパラメータを推定します。政策 π\piπ が状態遷移に影響を与えることで、系のダイナミクス(時間的推移)が制御されることを反映しています。また、観測 sss は状態 xxx に依存して生成され、これが観測モデルにおける尤度の形で表現されます。
5. まとめ
離散系モデルにおける自由エネルギー原理の実装は、感覚入力と隠れ状態が離散値を取る点を除いて、連続系モデルと同様の考え方で説明できます。生成モデル、変分自由エネルギー、期待自由エネルギーといった概念を用いることで、エージェントが外界を推論し、行動を生成するプロセスを統一的に理解することができます。
5. まとめ
離散系モデルにおける自由エネルギー原理の実装は、感覚入力と隠れ状態が離散値を取る点を除いて、連続系モデルと同様の考え方で説明できます。生成モデル、変分自由エネルギー、期待自由エネルギーといった概念を用いることで、エージェントが外界を推論し、行動を生成するプロセスを統一的に理解することができます。
