
正規分布について
正規分布の定義
正規分布は、データが平均値を中心に対称に広がる、統計学で最も重要な確率分布です。自然界や社会現象の多くのデータは、特に大量のデータを集めると、この分布に従う傾向があります。正規分布を理解することは、データ分析や統計的な推測を行うための基礎となります。

正規分布は、データの散らばり方を表す数学的なモデルです。平均値μと標準偏差σという2つの数値で特徴付けられ、データがどのように分布しているかを定量的に示します。特に、平均値が0で標準偏差が1の正規分布は標準正規分布と呼ばれ、様々なデータ分析に役立ちます。正規分布の数学的な表現は、データの性質を深く理解し、分析するための強力なツールとなります。

正規分布のグラフは、釣鐘型で、真ん中の平均値を中心に左右対称に広がっています。これは、データの大部分が平均値付近に集まり、極端な値が少ないことを意味します。グラフの広がり方は、データのばらつきを示す標準偏差によって決まります。標準偏差が大きいほど、グラフは広く、データのばらつきが大きくなります。
正規分布は、18世紀にガウスによって発見され、「ガウス分布」とも呼ばれます。彼は天文学や物理学のデータ分析で正規分布の重要性を示し、統計学の発展に大きく貢献しました。
正規分布は、身長や体重、テストの成績など、自然や社会現象の多くのデータに当てはまります。この性質を利用して、統計的な推測や仮説検定を行うことができ、様々な分野で活用されています。データ分析の基本を理解するためには、正規分布について学ぶことが重要です。

正規分布の特徴
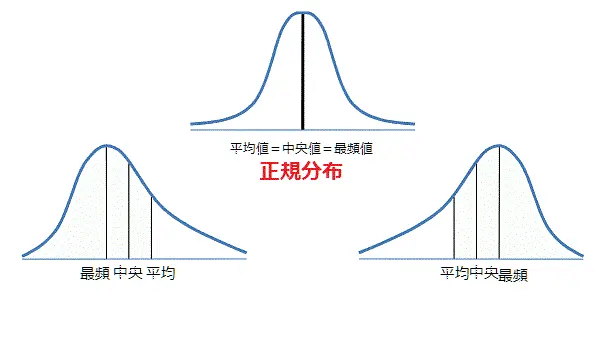
正規分布は、データ分析において非常に重要な役割を果たす、最も一般的な確率分布の一つです。その特徴は、データが平均値の周りに左右対称に分布し、平均値、中央値、最頻値がすべて一致することです。
平均値、中央値、最頻値の一致は、データの中心的な傾向を示す指標がすべて同じ値になることを意味します。これにより、データの分布を理解しやすくなり、分析や解釈が容易になります。例えば、身長や体重などのデータは、多くの場合、正規分布に近似されます。
左右対称性は、データが平均値の周りに均等に分布していることを示し、外れ値の影響を受けにくいという利点があります。これは、多くの統計的手法の基盤となる重要な特性です。
エンピリカルルールは、正規分布の特性を理解する上で非常に役立ちます。このルールによれば、データの約68%は平均値プラスマイナス1標準偏差の範囲に、95%は平均値プラスマイナス2標準偏差の範囲に、99.7%は平均値プラスマイナス3標準偏差の範囲に収まります。これは、データの大部分が平均値の近くに集中していることを示しており、異常値や外れ値の影響を考慮する際に役立ちます。
無限の範囲を持つ理論的な分布ですが、実際には極端な値はほとんど現れません。これは、正規分布が多くの自然現象や社会現象において適切なモデルであることを示しています。例えば、身長や体重、テストの点数など、多くのデータは正規分布に近似されます。
確率密度関数は、特定の平均値と標準偏差を持つ正規分布の形状を決定する数学的な式です。この関数は、特定の値が出現する確率を示し、データの分布を視覚的に理解するための重要なツールです。実際のデータ分析では、この関数を用いて、特定の範囲内にデータが存在する確率を計算することができます。
正規分布は、データ分析において非常に強力なツールであり、その特性を理解することで、データの分布をより深く理解し、より正確な分析を行うことができます。
正規分布の重要性
正規分布は、統計学において最も重要な分布の一つであり、多くのデータ分析の基礎となっています。データが正規分布に従う場合、平均値、中央値、最頻値が一致し、データの約68%が平均値からプラスマイナス1標準偏差の範囲に収まるという特徴があります。これにより、データのばらつきを理解しやすくなり、統計的な推測をより正確に行うことができます。
マーケティングリサーチでは、消費者の行動や嗜好を分析する際に、正規分布を用いてデータをモデル化することが一般的です。これにより、製品の需要を予測したり、効果的なマーケティング戦略を立案したりすることができます。
自然現象のモデル化においても、正規分布は広く利用されています。身長、体重、テストの成績など、多くの自然現象は正規分布に従うと仮定されます。この仮定に基づいて、科学者や研究者は観測データから一般的な傾向を導き出し、予測を行うことができます。
中央極限定理は、正規分布の重要な性質を示す理論であり、サンプルサイズが大きくなると、サンプル平均が正規分布に近づくことを示しています。この理論により、元のデータが正規分布に従わなくても、十分なサンプルサイズがあれば、サンプル平均は正規分布に従うと期待できます。
品質管理においても、正規分布は重要な役割を果たしています。製造業では、製品の品質を維持するために、工程のばらつきを管理する必要があります。正規分布を用いることで、製品の特性がどの程度の範囲に収まるかを把握し、異常値を特定することができます。これにより、製造プロセスの改善や、顧客満足度の向上につながる施策を講じることが可能になります。
正規分布の応用例
正規分布は、心理学、経済学、自然科学、医療、教育など、様々な分野で広く活用されています。
心理学では、知能指数(IQ)の分布が正規分布に近いことから、個人の知能を他者と比較することができます。この分布に基づき、IQテストの結果を解釈し、教育や職業選択の判断材料として役立てられています。
経済学では、株価の変動や収入の分布を分析する際に、正規分布が仮定されることが多いです。これにより、投資家はリスクを評価し、期待リターンを計算することができます。また、経済モデルの構築や政策決定にも役立っています。
自然科学では、測定誤差や生物学的特性の分布を分析する際に、正規分布が用いられます。例えば、物理学の実験では、測定値に含まれる誤差を正規分布で評価することで、データの信頼性を確認できます。また、身長や体重などの生物学的特性も正規分布に近いことから、集団の特性を理解することができます。
医療では、血圧や体温の分布が正規分布に従うことが多いです。これにより、医師は患者の健康状態を評価し、治療方針を決定することができます。例えば、正常血圧の範囲を基準として、高血圧や低血圧の診断が行われます。
教育では、試験の得点分布を分析する際に、正規分布が仮定されることがあります。多くの標準化されたテストでは、受験者の得点が正規分布に従うと考えられています。これにより、教育機関は合格基準を設定し、受験者の学力を評価することができます。
このように、正規分布は様々な分野で重要な役割を果たしており、データの解釈や分析、予測などに役立っています。
標準正規分布とは
標準正規分布は、平均が0、標準偏差が1の特別な正規分布で、データの散らばり方を理解する上で重要な役割を果たします。この分布は左右対称で、中央にピークを持ち、データの大部分は平均値の周りに集中しています。そのため、多くの自然現象や社会現象をモデル化するために利用されています。
Zスコアは、標準正規分布を用いてデータの場所を示す指標です。データポイントが平均値からどれだけ離れているかを標準偏差の単位で表します。Zスコアが0なら平均値と一致し、正の値は平均値より大きく、負の値は平均値より小さいことを示します。異なるデータセットを比較したり、統計分析を深めたりする際に役立ちます。
任意の正規分布は、標準正規分布に変換できます。これは標準化と呼ばれ、異なるスケールや単位を持つデータを比較する際に特に有効です。元のデータから平均値を引き、その結果を標準偏差で割ることでZスコアを計算します。これにより、すべてのデータポイントが同じ基準で評価され、統計分析の一貫性が保たれます。
標準正規分布は、統計的検定や信頼区間の計算において重要な役割を果たします。例えば、t検定やカイ二乗検定などの多くの統計的手法は、データが正規分布に従うことを前提としています。また、信頼区間を計算する際にも、標準正規分布を用いて母集団のパラメータを推定します。このように、標準正規分布はデータ分析の基盤となっています。
標準正規分布表は、Zスコアに対応する確率を示す便利なツールです。この表を使用することで、特定のZスコアに対する累積確率を簡単に確認でき、データの分布を理解するのに役立ちます。例えば、Zスコアが1.96の場合、約97.5%のデータがその値以下であることを示します。この情報は、統計的検定や信頼区間の計算において非常に重要であり、データ分析の精度を高めるために広く利用されています。

正規分布と標準偏差
標準偏差は、データのばらつき具合を示す重要な指標です。データが平均値からどれだけ離れているかを測ることで、データの散らばり具合を把握できます。標準偏差が小さいほど、データは平均値の周りに集まっており、大きいほど、データは広くばらついています。
標準偏差の計算は、まずデータの平均値を求め、各データと平均値の差を二乗し、その平均値を求めます。最後に、その値の平方根を求めることで標準偏差が得られます。この計算は、データのばらつきを定量的に評価するための基本的な方法です。
標準偏差は、データ分析や意思決定において重要な役割を果たします。例えば、テストの点数の標準偏差が大きい場合、学生の成績は大きくばらついていることを示します。逆に、標準偏差が小さい場合は、ほとんどの学生が似たような成績であることを示します。
信頼区間は、標準偏差を用いてデータの不確実性を評価する手法です。母集団の平均を推定する際に、標準偏差に基づいた信頼区間を計算することで、推定値の信頼性を示すことができます。例えば、95%の信頼区間は、真の平均がその区間内に存在する確率が95%であることを示します。
異なるデータセットのばらつきを比較する際にも、標準偏差は有効です。例えば、異なる地域の気温データを比較する場合、各地域の標準偏差を計算することで、どの地域が気温の変動が大きいかを判断できます。このように、標準偏差はデータの特性を比較するための強力なツールです。


正規分布の計算方法
データの分析において、平均、分散、標準偏差は重要な指標です。平均はデータの中心的な傾向を表し、すべてのデータの合計をデータの数で割ることで計算できます。例えば、生徒のテストの平均点は、全員の点数を合計して生徒の数で割ることで求められます。
分散はデータのばらつきを示す指標です。各データと平均の差を二乗し、その二乗値の平均を求めることで計算されます。分散が大きいほど、データは平均から大きく離れており、小さいほど平均に近いことを意味します。例えば、異なるクラスのテスト結果を比較する場合、分散はどのクラスの成績がより均一であるかを判断するのに役立ちます。
標準偏差は分散の平方根であり、データのばらつきをより直感的に理解するための指標です。標準偏差が小さいほど、データは平均に近い位置に集中しており、大きいほどデータは広範囲に分布していることを示します。例えば、製品の品質管理において、標準偏差は製品の一貫性を評価するのに役立ちます。
正規分布は、多くのデータセットに見られる一般的な分布パターンです。正規分布では、データの約68%が平均から1標準偏差以内に、95%が2標準偏差以内に、99.7%が3標準偏差以内に収まります。この特性を利用することで、特定の範囲にデータが存在する確率を簡単に計算できます。
エクセルは正規分布の計算を容易にするツールです。NORM.DIST関数を使用すると、特定の値に対する確率を計算できます。また、NORM.INV関数を使用すると、特定の確率に対する値を逆算できます。これにより、データ分析や統計的推測を行う際の効率が大幅に向上します。

正規分布の限界
正規分布は、データが左右対称に分布していることを前提としています。しかし、現実世界のデータは必ずしも対称ではなく、偏りがある場合があります。例えば、収入データは高収入層の影響で右に偏りがちです。このような非対称なデータに正規分布を当てはめると、誤った分析結果が得られる可能性があります。
また、データの中に極端に大きい値(外れ値)が含まれている場合も、正規分布は適切ではありません。外れ値はデータの分布を歪ませ、平均値などの統計量に大きな影響を与えます。例えば、実験データに誤った測定値が含まれていると、平均値がその誤った値に引っ張られてしまい、データの真の姿を表せなくなってしまいます。
さらに、データが複数のピークを持つ場合(多峰性)も、正規分布は適切ではありません。これは、データが複数の異なるグループから構成されていることを示唆しており、それぞれのグループに適した分布を考慮する必要があります。例えば、学生の試験結果が複数の学習方法によって異なる分布を示す場合、正規分布ではなく、それぞれの学習方法に対応した分布を考慮する必要があります。
現実世界のデータは、理論的な正規分布に完全に一致することは稀です。データに偏りや外れ値、多峰性などの特徴がある場合は、正規分布以外の適切な分布を選択する必要があります。例えば、右に偏ったデータには対数正規分布が適しています。データの特性に合わせて適切な分布を選択することで、より正確な分析結果を得ることができます。


bellcurve.jp
avilen.co.jp
mathnyumon.com
mathlandscape.com
m.youtube.com
wangcc.me
avilen.co.jp
#平均
#標準偏差
#確率密度関数
#標準正規分布
#中心極限定理
#累積分布関数
#対称性
#標準化
#ベル曲線
#札幌
#豊平区
#平岸
#鍼灸
