
モンティホール問題から学ぶ確率と統計
モンティホール問題の概要
モンティホール問題は、アメリカの人気ゲームショー『Let's Make a Deal』に由来し、司会者モンティ・ホールがプレイヤーに選択を促す場面から生まれました。この問題は、確率論の中でも特にベイズの定理や条件付き確率の理解を深めるための重要な例題とされています。多くの人々が直感的に誤解しやすいこの問題は、確率論のパラドックスを体現しており、数学者や一般の人々の間で長年にわたり議論を呼んでいます。
問題の設定はシンプルです。プレイヤーの前には3つのドアがあり、そのうち1つには当たりの景品が隠されています。プレイヤーは最初に1つのドアを選び、その後、司会者が残りの2つのドアのうち1つを開けて、必ずヤギがいることを示します。このプロセスは、プレイヤーに新たな情報を提供し、選択を再考させる重要な要素となります。司会者が開けるドアは常にハズレであるため、プレイヤーは残ったドアの選択を再評価することが求められます。
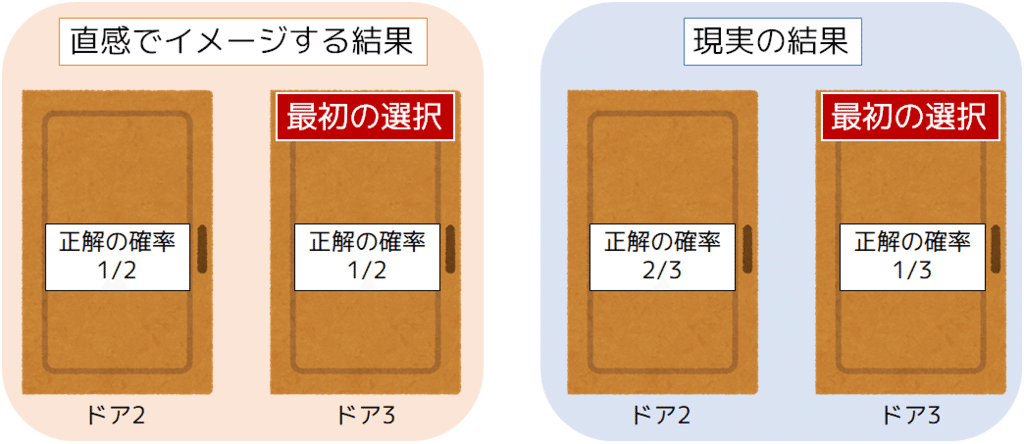
プレイヤーは、最初に選んだドアをそのままにするか、残ったドアに変更するかを選択できます。この選択が当たりを引く確率にどのように影響するかが問題の核心です。直感的には、残った2つのドアのいずれかが当たりである確率は1/2のように思えますが、実際にはドアを変更することで当たりを引く確率が2/3に上昇します。これは、最初に選んだドアが外れである確率が2/3であるため、変更することで当たりを引く可能性が高まるからです。
この問題は、直感的にはどちらのドアを選んでも確率は1/2のように思えますが、実際にはドアを変更した方が当たる確率が高くなるというパラドックスを含んでいます。この現象は、確率論における直感と論理の乖離を示す良い例であり、多くの人々がこの問題に対して納得できない理由の一つです。モンティホール問題は、確率論の理解を深めるための重要な教材として、教育現場でも広く利用されています。
条件付き確率の基本
条件付き確率は、特定の事象が発生した場合における他の事象の発生確率を示す重要な概念です。例えば、事象Aが発生したときに事象Bが発生する確率は、 $${P(B|A)}$$と表されます。この考え方は、日常生活の多くの場面で応用され、特に医療やリスク管理の分野で重要な役割を果たします。条件付き確率を理解することで、より正確な意思決定が可能になります。
モンティホール問題は、条件付き確率の理解を深めるための典型的な例です。この問題では、プレイヤーが最初に選んだドアの背後にある賞品の確率が、司会者がハズレのドアを開けることでどのように変化するかが焦点となります。具体的には、選ばれたドアが当たりである確率は$${1/3}$$であり、残りのドアのうち一つが当たりである確率は$${2/3}$$に増加します。この現象は、直感に反する結果をもたらし、条件付き確率の重要性を示しています。
モンティホール問題において、最初に選んだドアが当たりである確率は$${1/3}$$です。これは、3つのドアのうち1つだけが当たりであるため、選択肢の中から当たりを引く確率を単純に計算した結果です。一方、選ばなかったドアの当たりの確率は$${2/3}$$に上昇します。このように、選択肢が減ることで、残った選択肢の確率がどのように変化するかを理解することが、条件付き確率の本質を捉える鍵となります。
司会者がハズレのドアを開ける行為は、モンティホール問題における条件付き確率の理解を深める重要な要素です。この行為によって、選ばなかったドアの当たりの確率が$${2/3}$$に集中します。これは、最初に選んだドアが外れている場合、残りのドアのどちらかが当たりである可能性が高まるためです。このように、情報が与えられることで確率がどのように変化するかを考えることは、条件付き確率の基本的な考え方を示しています。
条件付き確率の計算は、ベイズの定理を用いることでより明確に理解できます。ベイズの定理は、事前確率を事後確率に更新するための強力な数学的手法です。この定理を用いることで、特定の条件が与えられた場合における事象の確率を計算することが可能になります。モンティホール問題においても、ベイズの定理を適用することで、選択肢の確率の変化を定量的に把握することができ、より深い理解を得ることができます。
ベイズの定理は、事前確率を事後確率に更新するための数学的手法であり、条件付き確率の理解において非常に重要です。この定理は、特定の条件が与えられた場合に、事象の確率をどのように修正するかを示します。モンティホール問題においても、最初に選んだドアが外れているという情報をもとに、残りのドアの当たりの確率を計算する際にベイズの定理が活用されます。このように、ベイズの定理は確率論の中で非常に強力なツールとなります。



ベイズの定理の応用
モンティホール問題は、確率論における重要な課題であり、特にベイズの定理を用いることでその解決が可能になります。この問題では、プレイヤーが選んだドアの背後にある当たりの確率を計算するために、事前の情報と新たに得られた情報を組み合わせる必要があります。ベイズの定理は、事象の確率を更新するための強力なツールであり、モンティホール問題の理解を深めるために不可欠です。これにより、プレイヤーがドアを変更した場合の当たりの確率を正確に算出することができます。
ベイズの定理は、事象Aが起こる確率を事象Bが起こった条件のもとで更新する方法を提供します。モンティホール問題においては、プレイヤーが選んだドアの背後に当たりがあるかどうかを判断するために、司会者がハズレのドアを開けたという情報が重要な役割を果たします。この情報をもとに、プレイヤーは選択を変更するかどうかを決定することができ、確率の計算が行われます。具体的には、最初に選んだドアが当たりである確率と、司会者が開けたドアの情報を組み合わせることで、選択を変更した場合の当たりの確率を導き出すことが可能です。
ベイズの定理を用いることで、プレイヤーがドアを変更した場合の当たりの確率が$${2/3}$$であることが示されます。この結果は直感に反するかもしれませんが、数学的には正しい解答です。最初に選んだドアが当たりである確率は$${1/3}$$であり、残りの2つのドアのうち1つが当たりである確率は$${2/3}$$です。したがって、プレイヤーが選択を変更することで、当たりを引く確率が高まることが明らかになります。このように、モンティホール問題は確率論の理解を深めるための優れた例であり、ベイズの定理の実用性を示すものでもあります。

期待値の計算方法
期待値は、確率論における重要な概念であり、特定の行動を繰り返した際に得られる結果の平均を示します。これは、特に不確実性のある状況において、意思決定を行う際の指針となります。期待値を計算することで、長期的な利益や損失を予測し、最適な選択をするための基盤を提供します。モンティホール問題においても、この期待値の概念が重要な役割を果たします。
モンティホール問題では、プレイヤーが最初に選んだドアを変更するかどうかが、期待値に大きな影響を与えます。最初の選択後、司会者が外れのドアを開けることで、残されたドアの当たりの確率が変化します。この状況において、ドアを変更することが期待値を高める戦略となるのです。期待値の観点から見ると、選択を変更することで、より高い成功確率を得ることが可能になります。
ドアを変更しない場合、プレイヤーが選んだドアが当たりである確率は$${1/3}$$です。このため、期待値も$${1/3}$$となります。つまり、ドアを変更しない選択をした場合、長期的に見れば、成功する確率は低く、期待される結果も限られたものになります。このことは、モンティホール問題の核心に迫る重要な要素であり、プレイヤーがどのように選択を行うかに大きく影響します。
ドアを変更する場合、期待値は$${2/3}$$に達します。これは、最初に選んだドアが外れである確率が$${2/3}$$であり、変更後のドアが当たりである確率が高まるためです。このように、ドアを変更することは、プレイヤーにとって有利な選択肢となります。期待値の計算を通じて、プレイヤーはより良い結果を得るための戦略を理解し、実行することができるのです。
期待値の計算は、意思決定のプロセスにおいて非常に重要です。特に、モンティホール問題のような不確実性の高い状況では、期待値を理解することで、プレイヤーはより合理的な選択を行うことができます。期待値を基にした意思決定は、長期的な成功を収めるための鍵となり、プレイヤーが直面する選択肢の中で最も有利なものを選ぶ助けとなります。
モンティホール問題において、期待値が高い選択をすることは、プレイヤーにとって非常に重要です。ドアを変更することで期待値が$${2/3}$$に上昇するため、プレイヤーはこの選択を行うことで、より良い結果を得る可能性が高まります。このように、期待値を意識した選択は、確率論に基づく合理的な判断を促し、最終的には成功を収めるための戦略となるのです。

直感と確率の対立
モンティホール問題は、アメリカのゲームショー「Let's Make a Deal」に由来する有名な確率論の問題です。この問題は、プレイヤーが3つのドアのうち1つを選び、司会者が残りのドアの中から1つを開けるというシンプルな設定から成り立っています。しかし、選択後の確率が直感に反する結果を示すため、多くの人々にとって理解が難しいものとなっています。特に、選択肢が2つに絞られた際に確率が均等になると考えるのは一般的な誤解です。これがモンティホール問題の核心であり、確率論の重要性を示す良い例です。
モンティホール問題において、プレイヤーが最初に選んだドアが正解である確率は$${1/3}$$です。残りの2つのドアのうち、1つは必ず外れであるため、プレイヤーが選ばなかったドアの正解確率は$${2/3}$$になります。このため、司会者が外れのドアを開けた後、残ったドアの正解確率は$${1/2}$$ではなく、選択を変更することで$${2/3}$$の確率で当たりを引くことができるのです。この直感に反する結果が、多くの人々を混乱させる要因となっています。
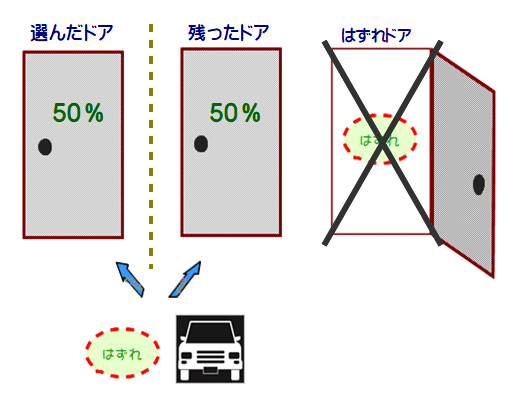
モンティホール問題は、直感と確率論の対立を象徴する問題です。多くの人は、選択肢が2つに絞られた時点で、残ったドアの確率が均等になると考えがちですが、実際にはそうではありません。この問題は、確率論がどのように直感を覆すかを示す重要な教訓を提供します。直感的な理解と論理的な思考の間に生じるギャップは、確率論を学ぶ上での大きな障壁となることがあります。
モンティホール問題では、選択肢が2つに絞られた際に確率が均等になるという直感は、実際には誤りです。プレイヤーが最初に選んだドアが正解である確率は$${1/3}$$であり、残りのドアの正解確率は$${2/3}$$です。このように、選択を変更することで当たりを引く確率が高まることを理解することは、確率論の基本的な考え方を学ぶ上で非常に重要です。直感に反する結果を受け入れることは、確率論を深く理解するための第一歩です。
モンティホール問題を通じて、確率論がどのように直感を覆すかを学ぶことができます。この問題は、確率論の基本的な原則を理解するための優れた教材です。特に、条件付き確率やベイズの定理の概念を用いることで、選択を変更することの利点を明確に示すことができます。これにより、プレイヤーは直感に反する結果を受け入れ、確率論の理解を深めることができるのです。
モンティホール問題は、確率論の理解を深めるための重要な教訓を提供します。この問題を通じて、プレイヤーは直感に頼ることの危険性を学び、論理的な思考を重視することの重要性を認識します。確率論は、日常生活のさまざまな場面で役立つ知識であり、モンティホール問題はその理解を促進するための優れた例です。これにより、プレイヤーはより良い意思決定を行うためのスキルを身につけることができます。
モンティホール問題の実験結果
モンティホール問題に関する実験は、理論的な結果を実証するために行われています。この問題は、条件付き確率の理解を深めるための重要な教材として位置づけられています。実験では、参加者が最初に選んだドアの後ろにある景品の確率を計算し、司会者が外れのドアを開けた後の選択肢の変化を観察します。これにより、理論と実践の相互作用が明らかになります。
多くの実験で、ドアを変更した場合の当たりの確率が$${2/3}$$であることが確認されています。具体的には、最初に選んだドアが正解である確率は$${1/3}$$であり、残りのドアのうち一つが正解である確率は$${2/3}$$に上昇します。この結果は、直感に反するものであり、多くの人々が理解するのに苦労しますが、実験を通じてこの確率の変化が明確に示されています。
実験結果は、理論と一致しており、ドアを変更することが最適な戦略であることを示しています。具体的には、ドアを変更した場合の正解確率は$${2/3}$$に達し、変更しない場合は$${1/3}$$に留まります。この明確な差は、参加者が選択を変更することの重要性を強調しており、確率論の基本的な理解を促進します。
これにより、モンティホール問題の解答が正しいことが実証されています。実験を通じて得られたデータは、理論的な予測と一致し、参加者が直感に反して選択を変更することが有利であることを示しています。この結果は、確率論の教育において重要な教訓を提供し、理論と実践の相互作用を強調します。
実験は、確率論の理解を深めるための重要な手段であり、理論と実践の橋渡しをする役割を果たします。モンティホール問題のような実験的アプローチは、学習者が抽象的な理論を具体的な経験に結びつける助けとなり、確率の概念をより深く理解するための基盤を提供します。これにより、学習者は確率論の複雑さを克服し、実生活における応用を見出すことができるのです。

統計学的な視点からの考察
モンティホール問題は、確率と統計の重要性を強調する優れた例です。この問題は、プレイヤーが3つのドアのうち1つを選び、司会者が外れのドアを開けた後に選択を変更するかどうかを問うものです。直感的には、選択肢が2つに絞られた時点で確率は$${1/2}$$になると考えがちですが、実際には最初の選択が正解である確率は$${1/3}$$、外れである確率は$${2/3}$$であることが示されています。このように、モンティホール問題は確率論の基本原理を理解するための優れた教材となっています。
統計学は、データを分析し、意思決定を行うための強力なツールです。モンティホール問題を通じて、プレイヤーは確率の概念や条件付き確率、期待値の重要性を学ぶことができます。特に、選択を変更することで当たりを引く確率がどのように変化するかを理解することは、実際のデータ分析や意思決定においても非常に有用です。この問題は、確率論の基礎を学ぶための実践的なアプローチを提供し、学習者にとっての理解を深める手助けとなります。
モンティホール問題は、教育現場でも広く利用されている確率論と統計学の応用例です。多くの教育機関では、この問題を通じて学生に確率の直感と論理的思考を養うことを目的としています。実際の授業では、シミュレーションやグループディスカッションを通じて、学生が自らの手で確率を体感し、理解を深めることが奨励されています。このように、モンティホール問題は、単なる理論的な問題にとどまらず、実践的な学びの場を提供する重要な教材となっています。

ja.wikipedia.org
manabitimes.jp
pref.kumamoto.jp
ja.wikipedia.org
bellcurve.jp
avilen.co.jp
manabitimes.jp
tech-teacher.jp
bellcurve.jp
nli-research.co.jp
qiita.com
kcg.edu
mas.kke.co.jp
note.com
ja.wikipedia.org
note.com
note.com
#確率 #条件付き確率 #ベイズ #期待値 #事前確率 #事後確率 #シミュレーション #データ分析 #意思決定 #論理的思考 #札幌 #鍼灸師
