
自由エネルギー原理の解説:知覚・行動・他者の思考の推論 5
連続系モデルとしての実装
一般化ガウシアン・フィルタリングでは、変分自由エネルギーの計算を簡単にするために、いくつかの近似を行います。
まず、事後確率を互いに独立と仮定する平均場近似を行います。
次に、解析計算を簡単にするために、期待値の周りで2次のテーラー展開による近似(ラプラス近似)を行います。
さらに、システムノイズと観測ノイズがガウス分布に従うと仮定します。
これらの近似により、隠れ状態とパラメータの事後確率はガウス分布として表すことができます。
そして変分自由エネルギーは、予測誤差と事前分布から計算される項で表すことができます。
予測誤差は、感覚入力と予測値のずれであり、脳内のニューロン活動として表現されます。
パラメータは、感覚入力と予測誤差に基づいて更新されます。 この更新則は、ヘッブ則に似た形をしており、神経回路網におけるシナプス可塑性のメカニズムと関連付けられています。
一般化ガウシアン・フィルタリングは、脳内で予測符号化がどのように実装されているかを説明するモデルの一つとして考えられています。
ポイント
連続系モデルは、時間的に連続な変化を扱うモデルです。
一般化ガウシアン・フィルタリングは、予測符号化を説明する連続系モデルの一つです。
変分自由エネルギーの計算には、いくつかの近似が用いられます。
予測誤差はニューロン活動として表現され、パラメータはヘッブ則に似た更新則に従って更新されます。
各式の解説とまとめ
変分自由エネルギーと変分作用
まず、以下の式は、変分自由エネルギーと変分作用を表しています。
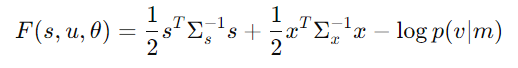

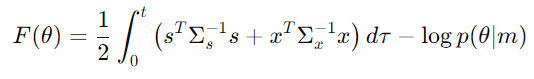

変分自由エネルギーは、感覚入力と現在の隠れ変数、パラメータが与えられたもとでの、外界のモデルの予測誤差を表しています。
変分作用は、過去から現在までの変分自由エネルギーを時間積分したものであり、パラメータの学習に用いられます。
更新則
次に、以下の式は、隠れ変数 u とパラメータ θ の更新則を表しています

ここで、
Du は、1 時刻前までの感覚入力から求めた隠れ変数の変化量の推定値、
f は隠れ状態のダイナミクスを、
g は感覚入力を決定する関数を表しています。
これらの更新則は、変分自由エネルギーを最小化するように導出されます。
隠れ変数の更新則は、予測誤差と事前分布に基づいて隠れ変数を更新する式であり、脳内での推論を表現しています。
パラメータの更新則は、過去の予測誤差と事前分布に基づいてパラメータを更新する式であり、脳内での学習を表現しています。
共分散行列

C-1u = ∂2F(s, u, θ)/∂u2 と C-1θ = ∂2F(θ)/∂θ2 は、それぞれ隠れ変数 u とパラメータ θ の事後確率の共分散行列の逆行列を表しています。
これらの式は、変分自由エネルギーの ヘッセ行列 に対応しており、事後確率の不確実性を表しています。
予測符号化モデル

ξs ≡ Σ-1s s = Σ-1s (s - g(Au)) と ξx ≡ Σ-1x x = Σ-1x (Dx̃ - f(Bu)) は、それぞれ感覚入力と隠れ状態の 予測誤差 を表しています。
ここで、
A と B はパラメータの行列、
g(Au) は感覚入力の予測値を、
f(Bu) は隠れ状態の予測値を表しています。
これらの式は、脳内での予測符号化を表現しており、予測誤差がニューロン活動として表現されていると解釈できます。
ニューロン活動

u̇ = Du + α (ATgξs + BTfξx + ∂log p(v|m)/∂u) は、隠れ変数の期待値をコードするニューロンの活動を表しています。
この式は、予測誤差と事前分布に基づいてニューロン活動が更新されることを示しており、予測符号化モデルのニューラルネットによる実装を表しています。
ヘブ型シナプス可塑性

上記は、パラメータ期待値 A と B の学習更新則を表しています。
これらの式は、予測誤差とニューロン活動の積に基づいてパラメータが更新されることを示しており、ヘブ型シナプス可塑性 を表現しています。
脳の謎を解き明かす「自由エネルギー原理」
私たちの脳は、世界をどのように理解し、行動を決めているのでしょうか?この謎を解き明かす鍵となる理論の一つに、「自由エネルギー原理」があります。自由エネルギー原理は、脳が外界の仕組みを模倣した「内部モデル」を構築し、そのモデルを使って予測と学習を行うことで、外界を理解しようとすると考えます。
私たちの周りには、光、音、匂いなど、様々な情報があふれています。脳はこれらの情報を五感を介して受け取り、処理しますが、その情報量は膨大で、そのままでは処理しきれません。そこで脳は、過去の経験から得られた情報に基づいて「内部モデル」を作り、そのモデルを使って未来を予測することで、効率的に情報処理を行っています。
自由エネルギーを最小化せよ!
自由エネルギー原理では、脳は常に「自由エネルギー」と呼ばれる量を最小化するように働いていると考えます。
自由エネルギーとは、簡単に言うと、「予測と現実のズレ」のことです。
脳は、内部モデルを使って外界を予測し、その予測が現実と一致すれば、自由エネルギーは小さくなります。
逆に、予測が外れると、自由エネルギーは大きくなってしまいます。
脳は、この自由エネルギーを最小化するために、常に予測の精度を高め、学習を続けているのです。
まとめ
自由エネルギー原理は、脳の働きを理解するための強力な枠組みを提供するだけでなく、人工知能、認知科学、精神医学など、様々な分野に大きな影響を与える可能性を秘めています。
今後、自由エネルギー原理の研究がさらに進展することで、脳の謎が解き明かされ、より人間らしい AI が誕生する日も、そう遠くないかもしれません。
