
【中3数学】展開をどう指導するか
新学期の喧騒も少し落ち着いてきた。
新学期は色々とザワザワするので、それと反比例するように学校の学習内容とペースは穏やかになることが多い。
生徒たちは新クラスの良し悪しやら、どの部活に入ったやら、選択科目の抽選に漏れたやら、新生活の一喜一憂を報告してくれるが
僕としてはこの時期は結構ヒマで、ゆっくり時間が流れる感じが割と好きだったりする。
で、この時期に中3は数学で「展開」という単元をやっている。
正直めちゃくちゃ簡単なので、点取りゲームの観点で言えばカモだ。
ただ、学力(数学力)の観点で言えば実は今後の計算の基盤をなす大事なところで、スポーツで言う基礎的な走りのフォームづくりに近い。
ちょうどウチの指導者が良い題材を挙げてくれたので、今回は展開指導の考察。
テーマ問題
題材に挙げてくれたのは
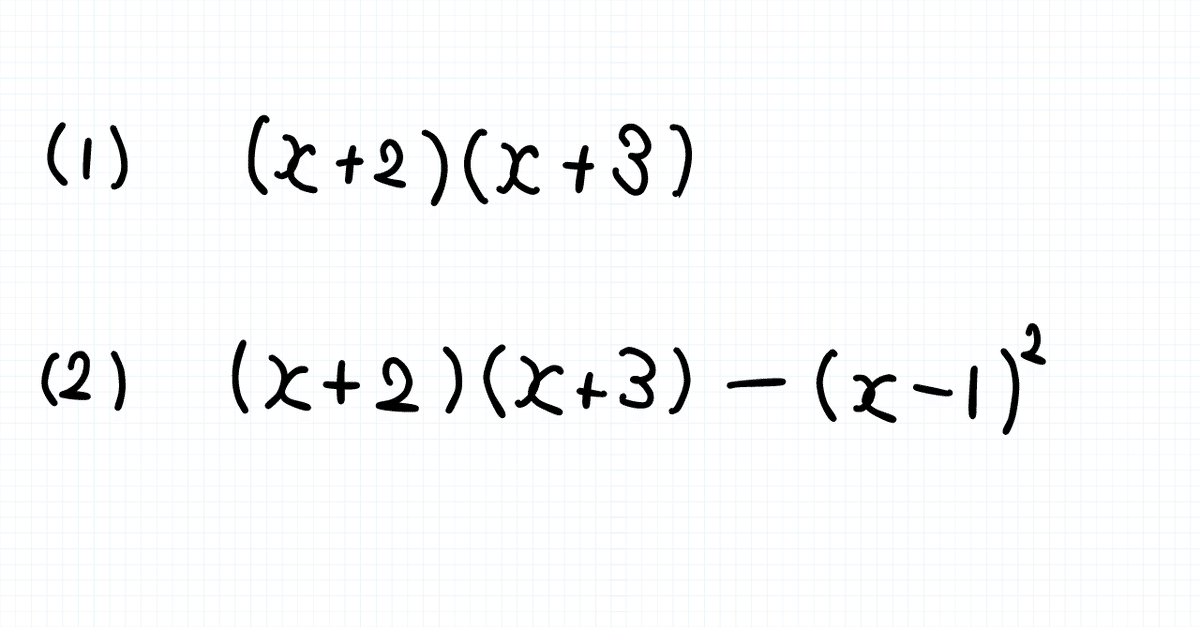
これの(1)は解けるが
(2)は解けないという生徒。
(1)は展開公式そのままの問題。
つまり典型パターンは解ける。
(2)は複数の展開公式がでてくる、複合問題というやつだ。
ヒアリングしたところ、(2)にも公式というか、定まった解き方があると思っていたらしい。
指導法①
ウチの指導者が選んだのは
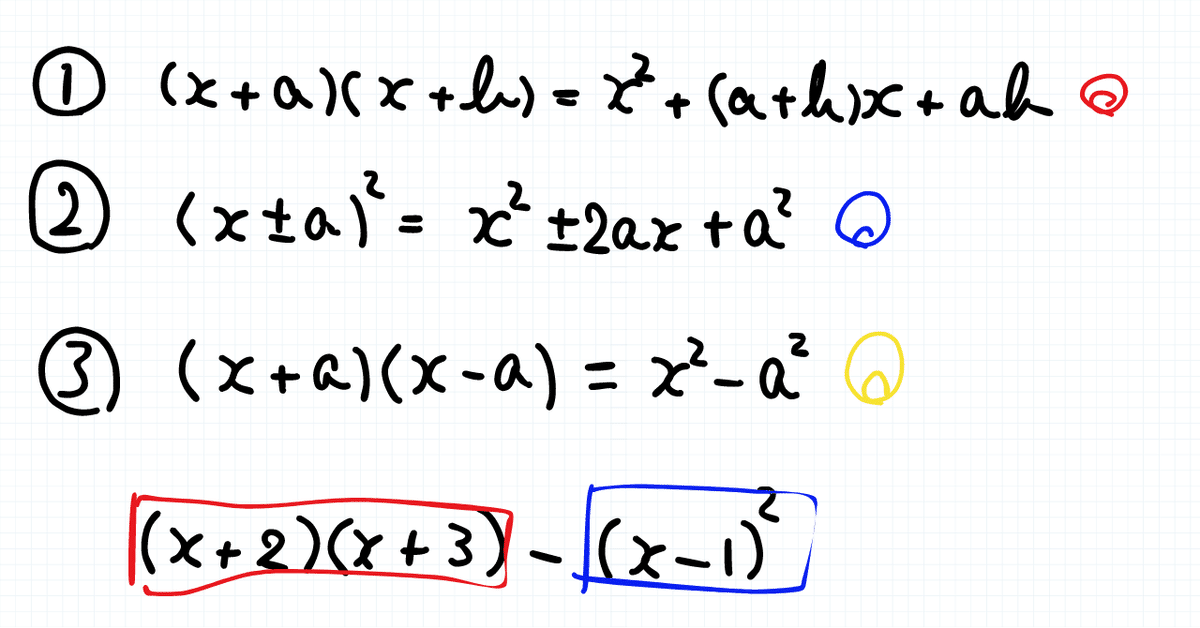
こんな感じで公式に色を設定して、生徒に色分けをしてもらうという方法。
これはこれで良い指導法だと思う。
主旨としては
「カタチに反応する」
といったところだろう。
数学にはカタチがある。
この見た目のものは、こう解く
という、将棋の定跡(手筋)に近いようなものだ。
基礎的な問題・頻出の問題についてはカタチとして覚え、それに反応するというのは数学ができる人に共通の特性だ。
今回の(1)のようにカタチがそのまま出題されていれば簡単だけど、(2)のような複合問題になった時に
「部分的に、ここはカタチだ」
という反応を起こせるかが重要になる。
そこにフォーカスを当てたトレーニングとして色分けはひとつの方法だと思う。
ちなみに色分けみたいなルールを設定して生徒の意識をトレーニングしたい認知過程に絞ってあげる方法はすごく使える。
画像だけだとなんだか子供っぽいし、薄い指導に思えるけど、実は理論的な背景もあって工夫の凝らされた指導だ。
指導法②
指導法①はそんな理由でちゃんと優秀だ。
ただ僕はそれを選ばないと思う。
というより、身も蓋もない話になってしまうけど、個人的な感覚として

これの(1)は解けるけど(2)は解けないという状況になってしまった時点でちょっと分が悪い感じがする。
将棋好きなので将棋風に言うと
「検討すべきはもっと前の局面」
ということだ。
僕は展開という単元については予習を推奨している。
まぁウチは生徒が自由に自分のやることを決めていい塾なので、僕の提案に乗っかる生徒もいるし、乗っからない生徒もいる。
それは生徒の判断なので別に良い。
提案に乗っかって予習することにした生徒にはまずこう言う
「じゃあ、これが展開という単元の問題だから。やってみ。」
すると生徒はかなりの確率でこう返す
「いや、習ってないし、やり方わかりません」
そこからは
「知らん。やってみ。」
「え…?」
「いや、ノリで。感覚で。なんかこうかなってことを書けばいいよ」
まぁ半分はふざけているのだけど、僕はふざけたノリに大事なメッセージを載せるのが粋かなって勝手な美学を持っているのでこういうやり方を好んで使う。
ここでのメッセージは
「数学は、解き方なんて知らなくても原則通りやっていたらだいたい解ける」
ということ。
(このやり取りがしたいがために、予習を推奨する)
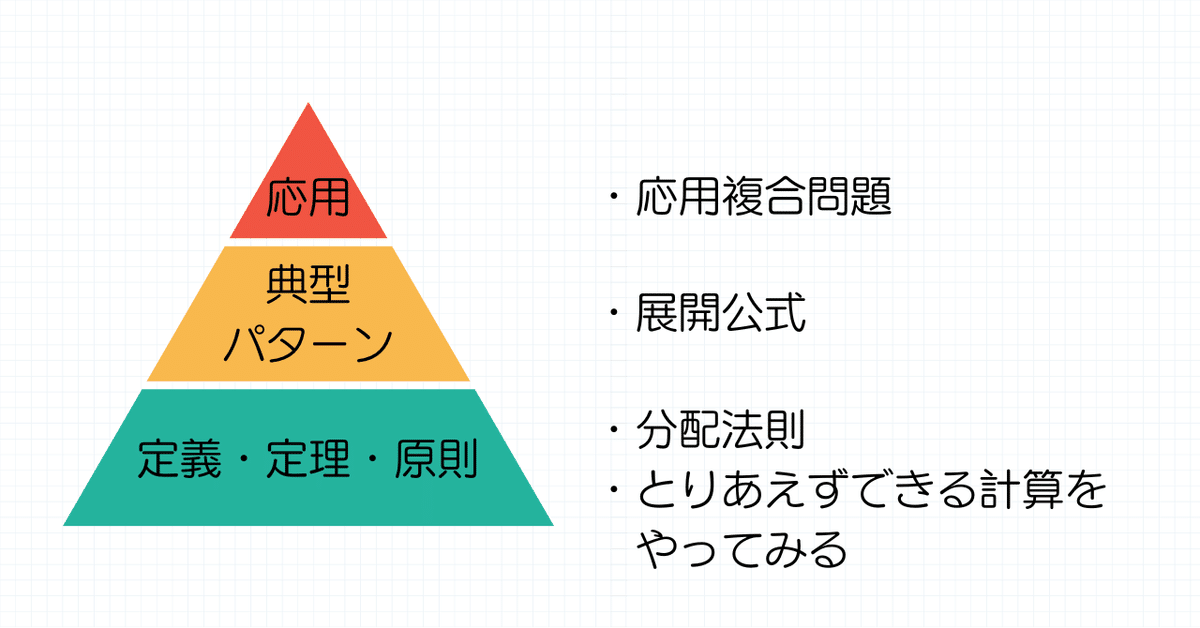
感覚的にはこんなイメージ。
数学という科目は、原理的に言えば定義を知っておけば全部解ける。
(ただ、現実的にこれは数学者レベルの思考力と発想力を要求するので、実際には典型パターンは知っておくべきなのだけど。)
「どんな問題でもとりあえずいつも通りやればいい。その中にたまたま知っているカタチが出たら知識を引っ張ってくる」
という感覚でやっている人と
「数学とは習ったカタチを習った通りに実践するものだ」
という感覚でやっている人では全く話が違う。
定義・定理・原則は数学力の土台だ。
典型パターンなどの「知識」はその上に載ってないと意味がない。

ピラミッドで図解したものを円で図解するなんて美しくないけど、なんとなくこんなイメージだ。
「習ってないし、知らないけど、とりあえず原則通りやってみよう」
という意識がある人は左。
こういう人は典型パターンから外れていても解ける。
鮮やかに解けるかは別にして、とりあえず答えまで辿り着けるし、多分それが数学力の大切な根幹だと思う。
一方で
「数学とは習った通りにやるものだ」
「習ってないものは解けない」
と思っている人は右。
典型パターンから外れると解けない。
さらにまずいのは、応用複合問題は単に典型パターンの足し算にはなっていないということだ。
今回の(2)で言うと、それぞれのパーツを展開公式でバラしたとしても、その後の計算は公式ではない。普通に原理通り計算する必要がある。
そもそも
「これは複合問題だ」
なんて解いてる時に認識なんてしていない。
指導法①の色分けトレーニングの場合
「この問題は複合問題だ」
ということは暗黙のうちに示されている。
生徒は
「これは複合問題だ。」
ということは記憶することになる。つまり典型パターンのような学習になる。
だから理想はやはり
「展開公式なんてない。全部ノリで解いているだけだ」
という感覚を持ってもらうことだと思う。
このファジーな感じが、数学力の本質だと思うけど、このファジーさは「指導」という行為としこたま相性が悪い。
空気で伝えるということ
ふざけたノリの中で伝えるのが美学だと書いたけど、単に美学なだけでなくて、ちゃんとした方の理由もある。
「いいかい。数学というのは習ったカタチをそのまま出す科目じゃないんだよ。未知の問題でも、これまでやってきた問題と類似させて、同じように解くことが大事なんだ」
と説くこともできる。
実際、そう言わないと伝わらない生徒もいるので、こういう説明をしたりもする。
(なんか負けた気になる)
でも、こんな形式ばった指導になると、それは形式ばった知識として生徒に入る感じがする。
外付けハードディスクにファイルを保存してる感じがする。
学習とは、もっと自然に、流れの中で発生するものだと思う。
子供たちは大人が当たり前のようにやっている振る舞いを見て学ぶ。
レジに並んで会計する姿
電車に乗る姿
電話に応答する姿
いろんな姿をみて
「あっ、これが当たり前のことなんだ」
と学び、静かに真似をする。
教えたことなどないはずのことが、自然にできるようになる。
数学を解く振る舞いも同じだと思う。
いかにも指導らしく
「これは、こうするものですよ」
と伝えるよりも
「まぁ、だいたいこんな感じかな?」
ってなにも語らずただ目の前で解いてみる。
「えっ?なんでそんなことしてるの?」
「なんでこうしないの?」
さも生徒が常識外れのことをしているかのように振る舞ってみせる。
これが、空気で伝えるということ。
僕には、展開の問題が解けずに固まっている生徒も、コンビニでレジに並ぶことを躊躇している子供も同じように見える。
必要なのは形式ばった知識ではなく、流れの中に存在する行動様式だ。
大人たちが初めて立ち寄った店でもモノを買いたければとりあえずレジを探すように
「まぁ、だいたいの場合はこうだろう」
という感覚で問題を解ける人が、本当に力がある人だ。
ファジーなことを、空気で伝えることができるのは生徒と1on1の会話の中で指導できる個別指導の特権だと思う。
まとめ/優先順位はなにか?
これまでの話をまとめると、
僕は指導の際に
「どんな問題でも原則通り(ノリで)やる」
という土台づくりを最優先する。
そして、その原則というのは決して形式ばった知識ではなくて、ある種の行動様式だ。ファジーなものだ。
だからそれを伝えるのに形式ばった指導は適さないと思う。
会話の流れの中で、自然に発生する空気によってそれを伝える。
僕の指導ではこの
ファジーな行動様式を伝える
というのがミソになっている。
今回は数学の解法だったけど、
僕が専門とする学習法、計画を立てることだったり、動画や参考書をどう使うということも、つまりは行動様式だ。
これは機械にはできないことだし、マニュアル化もできない。
そもそも指導者自身が、学習者として良質な行動様式を持っていることが前提になる。
自助努力も含めて要する労力で言えばものすごくコスパが悪いことだけど、だからこそ均質化された指導を広く展開する大手塾には出せない価値を提供できると自負している。
なにより、ロマンと美学があって僕は好きだ。
