第12回　情報源符号化　その１

阿坂先生
今回は情報源符号化の第１回目じゃ。情報源符号化の勉強では、より多くの記号をできるだけ少ない０と１のビット列で（送る）保存する！という課題を取り扱うぞい。

桂香助教
たとえばね、「AAAAAAAAAAAAA・・・・AAAAAAA」といった記号Aが1000個続く情報をハードディスクに保存したり、インターネットで誰かに送ったりするときに「Aを保存し（送り）続ける」よりも、例えば「Aが1000個」と表現して保存した（送った）ほうがハードディスクや通信量を節約できる。うまい具合に保存して（伝送して）情報を減らせないか？この例は極端だけど、今回はできるだけビット数を減らすのがテーマよ。

麦わら君
はい。わかります。いわゆる情報の圧縮ってやつでしょうか？動画ファイルでサイズが大きいとあっという間にハードディスクが一杯になってしまうので圧縮したいなと思うことがよくあります。zipファイルやlzhファイルのような圧縮をイメージすれば良いですか？

阿坂先生
そうじゃ。電子メールを送ろうとしたときに添付ファイルのサイズが大きすぎて送れなかった経験はないかな？そんなとき、ファイルのサイズを小さくしたいと思うはずじゃ。情報源符号化の勉強はそれを可能とする符号化技術というものを勉強する。

桂香助教
情報源符号化による情報圧縮は応用範囲が広いのよ。今回はこの情報圧縮の基礎について考えていくわ。

阿坂先生
情報源符号化を勉強していくには符号とは何かを知る必要がある。じゃが、ここでは、深入りを避けて符号とはある記号を０と１で表現するものと考えてみよう。記号はなんでも良いのじゃが、ここではＡ,B,C,Ｄの４つにしてみよう。例えば記号を以下のように０と１で表してみたぞぃ。

麦わら君
何かの情報（記号）をデジタルに変換しているイメージですか？

桂香助教
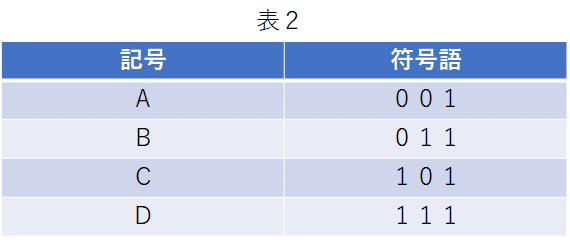
この段階ではそう考えても良いわ。記号をできるだけ少ない０と１とを使って保存（伝送）しようとするのが今回の目標よ。記号を０と１で符号を使った表したものを符号語、符号語のビット数を符号語長ということにする。以下は、無駄に符号語が長い悪い例（符号語長３）よ。

麦わら君
上の例は符号語の最後に無駄な1ビットがついていますね。でも表１のように４つの記号を表すのには少なくとも２ビット（符号語長２）は絶対に必要じゃないですか？これ以上短くできるのですか？これが1ビット（符号語長１）にできるなら凄いことですけど・・・。

阿坂先生
たしかに4通りの全記号を表現しようとすると2の2乗個の2ビットが必要となる。しかし、平均的な符号語長については短くできる可能はある。ヒントはエントロピーにあるのじゃ

麦わら君
うーん。エントロピーですか？エントロピーは曖昧さだから曖昧じゃない場合・・・つまり発生確率が偏る場合、ビット数を削減できるのかな？

桂香助教
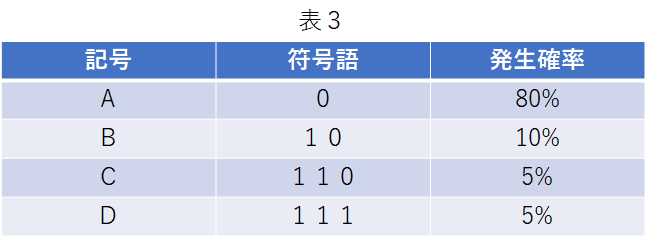
するどい！だいぶ情報理論に慣れてきたんじゃない？発生確率が分かっている以下の例を考えてみるわ。例えば、発生確率がＡが80%,Bが10%,Cが5%,Dが5%として、以下のように符号語を割り当てる。

麦わら君
上記のどうやって符号語は決めたのですがか？それにAは符号語長１だけどCとDの符号語長は逆に３と増えてますけど？

阿坂先生
符号語の作り方は次回に勉強する。表３は符号語長は記号によって１～３と異なっているが、１記号あたりの平均符号長はいくらになるかのぉ？

麦わら君
え？平均符号語長ですか？（1+2+3+3)/4=2.25ですか？これでいいですか？

桂香助教
単純な平均じゃなくて発生確率も考えるが情報理論だったわよね。Aの符号語長は１でそれが発生する確率は80%、Bの符号語長は２でそれが発生する確率は10%で・・・というふうに考えてやると１記号あたりの平均符号語長Ｌは

Ｌ＝１×0.8 ＋ 2×0.1 + 3×0.05 + 3×0.05 =1.3

になる。平均符号語長Lは1.3よ。Lは２より小さくなる。記号が４つあるからといっても平均符号語長Lは2よりも小さくできる可能性がある。

麦わら君
なるほど。ふっふっふ。見えてきました。発生確率に偏りを利用しているんですね。つまり、エントロピーが小さいほど平均符号語長が短くなりそう。

阿坂先生
そのとおりじゃ。平均符号語長Lを短くするコツは「発生確率が大きい記号には短い符号語を。発生確率が小さい記号には長い符号語を割り当てるのじゃ」のじゃ。

桂香助教
そして、エントロピーHと平均符号語長Lの関係だけど、Lがどこまで小さくできるかというとHが限界となる。Lの限界がHになるって凄いと思わない？

阿坂先生
ちょっと計算してみよう。表3のエントロピーを計算してみるのじゃ。LはHよりも大きくなっているはずじゃ。

麦わら君
エントロピーHは

H＝0.8×log(0.8) + 0.1×log(0.1) + 0.05×log(0.05) + 0.05×log(0.05) =1.02

確かにL≥Hですね。限界値としては、上手に符号化してやれば平均符号長Lを1.02まで小さくできるということですか？でもどうやって？

桂香助教
それを理解するには次回の符号の作り方と拡大情報源というものを勉強する必要があるわ。ここではできるだけ言っておくわ。

阿坂先生
重要な定理をまとめて今回は終わりにしよう。エントロピーHと平均符号語長Lの関係は

H≤L

じゃ。これを情報源符号化定理という。

桂香助教
これの意味するところはある記号を表すのに必要なビット数の下限値はその情報のエントロピーよりも小さくはできない。逆に言うと「どうにかこうにか」すればエントロピーまでは近づけることができるとも言えるわ。

麦わら君
なるほど・・・。エントロピーＨって情報の量の期待値でしたよね。だから平均符号語長Ｌが情報の量の平均値の長さ（ビット数）になればHと同等になるってことか。

阿坂先生
情報源符号化定理のイメージは上記のようなざっくりしたもので大丈夫じゃ。厳密な定義を知りたい場合は教科書を参照して欲しいぞぃ。

桂香助教
今回は表３のように符号語を作ったけど、次回は符号語の作り方を勉強していくわ。そして、符号語長ＬをエントロピーＨに近づけていく方法についても勉強していくわ。