
数学が嫌いだけどできるようになりたい人が見る取扱説明書③
↑↑前回の続きになっています.是非ご覧ください.
↑↑初めて来られた読者は最初から閲覧することをおすすめします.
前回は暗記科目と数学の問題構造の違いを説明したうえで実際に例題を使って解答のプロセスをチャート図を使って整理した.
チャート図から大まかであるが数学は暗記科目教科に比べて問題構造が遥かに複雑で問題構造の層と言われる知っているか思いつかないかで分岐する箇所が多いことが分かった.
わざわざ前提として知って欲しいことという項目まで使って説明したのには訳がある.
今回はなぜ多くの人が数学を難しい,嫌いと感じてしまうのかを問題構造の観点で詳しく解説していこうと思う.
1.数学:問題構造の層が多いが故の問題点
数学は問題構造の層(知っているか思いつかないで分岐する箇所)が暗記科目に比べて遥かに多いことは前回例題を用いて解説した.問題構造の層が非常に多いことが数学の苦手さや難しさにどのように影響するのかを論理的に解説する.
問題点(1):数学は未到達の問題構造の層を放置しやすい科目
問題構造の層が多いと起こる問題の1つとして思いつかないが故に途中で回答を諦めてしまう傾向が強くなってしまい,結果として未到達の問題構造の層を生んでしまうということだ.
日本語だけで説明しても全く意味が分からないと思うので具体例を交えて説明する.
①暗記科目教科の場
前回も用いた日本史の例題解説で使用した解答のプロセスチャート図を用いて説明する.
例えば生徒Aさんが上図のような日本史の問題を演習の時間に出題されたと仮定する.
Aさんは初見(1回目)で解いた時に次のように考え解答用紙に該当する番号をマークした.
Xの部分では栄華物語の知識は抜けていたのでb以外を選択した.
Yの部分では本居宣長についてきちんと勉強したのでcを選択した.
上記の内容を解答のプロセスチャート図に沿って整理すると
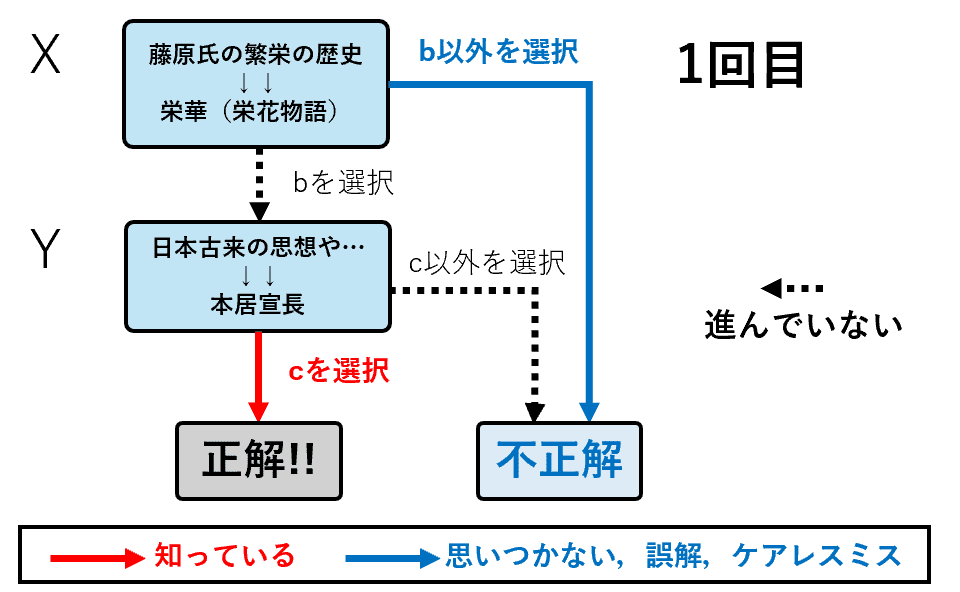
①Xではb以外を選択したので青い矢印に進む
②Yではcを選択したので赤い矢印に進む
③それら以外の矢印は黒点線で進んでいない矢印として表現されている
チャート図を見てみるとXの時点で青の矢印に進んでいるためこの時点でAさんが解いた例題は不正解である.
しかしYではちゃんと正解の選択肢であるcを選んでいるため.Xの部分(藤原氏の繁栄の歴史を描いたものは栄花物語であるということ)を知識として定着させれば次例題に挑戦した時正解を導くことができる.
次にAさんは解答解説をしっかり読み込み「藤原氏の繁栄の歴史を記したものが栄華物語」であることを知識として習得した.
すると2回目に同じ例題を取り組むときはXの部分でしっかりbを選択する.またYの部分は知識として本居宣長は知識として存在するのでcを選択.

結果:X,Yどちらも赤い矢印へと進み,2回目でようやく正解の解答にたどり着いた.
このように一問一答形式の暗記科目教科はたとえ解答を間違ったとしても解答解説を読めば自分の思いつかなかった知識,間違った知識に気がつきやすく軌道修正しやすいのである.
問題構造の層が少ないと要求される知識や解答解説を読んで修正をかけるポイントがそもそも少なくなる.また解答解説も分かりやすくとてもシンプルな構成で自分の間違った部分を簡単に見つけられる.
一方で数学はどのようになってしまうのだろうか?
②数学の場合
今回もAさんには日本史と同様に数学の例題を演習の時間に出題されたと仮定する.
Aさんは円周角の定理を用いて角ABE=角BACであること.二等分線の性質を用いて角ABD=角CADであること.さらに二等辺三角形から角ABC=角ACBとAD=BDであることは演習中に思いつきそれらを計算用紙に記述した.
しかしAさん△ABDから外角の公式を使って角BCDを導き出す方法が演習中に思いつかず,△ABCと△CBDが相似関係であることが思いつくことなく終了し余白でいっぱいになってしまった.
数学の苦手な皆さんはもちろん比較的得意である筆者でさえもこういうケースは良くあることだ.

上記の内容をフローチャートで再度まとめた.△ABDから外角の公式を使って角BDCの角度を求めるのは④に該当する.それを踏まえてチャート図では
④は△ABDから外角の公式を使用することが思いつかなかったので青い矢印に進む
①~③,AD=BDはそれぞれ計算用紙に記述し間違っていなかったので赤い矢印に進む
④が思いついていないため①~④全ての項目が分からないと相似条件は示せない.そのため青い矢印に進む
これら以外は進んでいない矢印を示し,進んでいない矢印で結ばれている問題構造の層は経由手段がないため未到達の問題構造の層と呼び,チャート図ではピンクの枠になる.
チャート図を見てもらえれば分かるが,④の外角の公式が思いついていないので三角形の相似を示せるわけがなく,不正解である.
日本史の例題とは異なり数学は一つの問題構造の層が思いつかなくなるとその時点で不正解(詰んでしまうこと)なのでそれ以降の問題構造の層が結局問題の中でAさんに解答されることもなく未到達の状態で終わってしまうことが良くある.
何を言っているのか分からないと思うので話をもう少し続けようと思う.
初見で問題を解いた際,外角の公式を思いつくことができず△ABCと△CBDが相似であることを証明できなかったAさんは例題の解答解説を読み自分のできなかった外角の公式と相似条件についての復習を行った.その後数学の例題に再挑戦した.(2回目)
外角の公式と△ABC,△CBDが相似であることは実際初見(1回目の段階)で①~③までは解答を作っていたのと初見の時復習を行っていたので証明することは簡単だった.しかし二つの△を相似であると示した後,相似関係を使って線分ADの長さを求めることができなかった.結果として不正解になった.
以上の結果を踏まえてAさんが2回目に解答したプロセスチャート図を見てみよう.

2回目では外角の和の公式と相似条件についての復習をしっかり行ったため④と相似条件の部分に赤い矢印とそれぞれの問題構造の層が未到達のピンク色から水色へと変化した.ようやく2回目にして未到達の問題構造の層にAさんは触れるようになった.
しかしAさんは三角形の相似は示したものの△ABCが二等辺三角形であることを利用し,ADの長さを求められていない.そのため未到達の問題構造の層が残っており,この層についてはAさんは一度たりとも解答を行ったことがない.
なのでここで仮に数学の例題に再挑戦することを諦めてしまった場合,未到達の問題構造の層については一切触れることなく次の問題へと進んでしまう.
もう少しピンと来るような表現に言い換えると映画で言うなら「2時間ちょっとの映画の一番興奮するクライマックスシーンを途中で見るのを止めて,次の映画を見ているようなもの」,サッカーで言うなら「スタジアムで観戦中,後半アディショナルの3分間で何としても1点を決めて勝ちに行きたいのに,このタイミングでスタジアムから離れるサポーター」と同義である.
勉強も映画もサッカーも共通して言えるのは「最後まで経験してないにも関わらず,途中で分かったつもりになって諦めている」ことである.
映画でも「どうせ最後のオチが大体読めるからつまらない」とかサッカーでも「たかが3分でゴールなんて決まらないから見たってしょうがない」と思うのと同じように勉強でも「どうせ解答を見てこんな感じで解く方法は大体分かったし,こんなもんでいいでしょ」と慢心すると特に数学は帰って痛い目を見る.
何故なら自分は解答を見て解いたつもりでもフタを開けたらまだ未到達の問題構造の層が存在しているケースが多々あるからである.
さらに数学の問題では未到達の問題構造の層が生まれてしまうが故の大きな欠点がある.それは経験値の差が生まれてしまうことである.
初見(1回目)での解答から2回目の解答を経て未到達の問題構造の層(ピンク)が少なくなったが,その未到達から既達になった問題構造は2回目の解答において初見で攻略したことになる.
つまり,初見で解けていた問題構造からすると2回同じ事を繰り返して解答プロセスを経ているため未到達の問題構造の層に比べて2倍になる.
このことによって経験値において差が生まれてしまい,数学の練習問題たくさんやったのにも関わらず,後半部分の問題で経験不足に陥り解答に行き詰ってしまうパターンになってしまう学生がとても多い.
数学の問題は大問の中に小問が複数に分かれて構成されているが,前半で解答した数値や原理を用いて後半の解答を考える問題形式が非常に多い.
そのため前半部分でつまづいてしまい,後半まで解答を考えることができず終わってしまった場合に
復習を行った際,前半部分で得られる学習経験値は豊富であるが後半にゆくにつれてどんどん少なくなってしまうパターンが非常に多い.
このように数学の問題は前半が分かったうえで後半へと話を進めていく問題形式が基本になるので,前半と後半で学習経験値に差が生まれ,知識の格差を非常に生みやすい.
実際にも高校数学において数学ⅠA,ⅡBで最も苦手な単元として「数列」や「ベクトル」を挙げる人が非常に多い.なぜならこれらの単元は教科書や大学共通テストや様々の入試問題で最後に登場する単元である.
特にテストにおいて「時間内に数列・ベクトルまでたどり着かなかった」と嘆く人は良く耳にするだろう.問題構造上最後にあるため数列・ベクトルまで到達した比較的数学が得意な学生のみがテスト内で次々と学習経験値を蓄積していく.
しかし最後までたどり着かなかった数学が苦手な学生は解答を見返さない限り永遠に数列・ベクトルにたどり着くこともなく,いつの日か数列・ベクトルに苦手意識を持つようになる.
最終的に数学が得意な人は数学の学習経験値をどんどん蓄積する環境を生み出していき,反対に数学が苦手な人は学習経験値が後にゆくにつれて無くなっていく.ここで得意な人と苦手な人で経験値格差を生んでしまう.
この話を聞いてどうして自分が数学が苦手かなんとなくわかった人もいるだろう.
数学というのは問題構造上「得意な人はますます得意になるように,苦手な人はますます苦手になるようなシステム」になっている.ここでは経験値格差という言葉を使って,数学の問題が後半にゆくにつれて得意な人と苦手な人とで知識を吸収できるチャンスに差が生まれてしまうことが分かる.
数学が苦手だと感じる人はまずこの「未到達の問題構造の層」を1つずつ,1つずつシラミつぶしに知識として習得していかなければならない.
そうでもしないと数学が得意な人との差は一向に埋まらないのである.
③閑話休題
ところでAさんが2回目に数学の例題を解くのを見て
「1度解答を見ているのだから正解まで解けて当然なのに,なぜ正解できない?Aさんってもしかしてバカ??」
とツッコミを入れたくなるかもしれない.気持ちは分かるが正直に言うと数学が苦手だと思う人に限ってこのように考えてしまう人は案外多い.自慢の記憶力の高さを生かして数学の解答を丸々覚えたことで数学ができたつもりになっているタイプが陥りやすい思考なので…上記のようにツッコミたくなった人は気持ちを改めていただきたい.
(このようなタイプの人に向けた対処法も後々解説します)
人間は何かを覚える際および間違っていたことを正しいことに修正する際は基本的に1回の助言で1つの事しか記憶できない(よくて2つ)と考えた方がよい.
スタンフォード大学の研究によるとマルチタスク作業者はシングタスク作業者に比べてパフォーマンスが低下するという結果が,脳科学においてもマルチタスク派は脳でシングタスクをスイッチのように切り替えているだけでシングルタスク派よりも作業効率が悪いという報告がされている.
「2兎追うものは1兎も得ず」という有名な「ことわざ」がある通り,複数の事をやってみようとしても返って効率が悪く無駄になってしまうことがある.

漫画に登場する「時を止める能力」を持つ吸血鬼がこれだけのマルチタスクでパンチをするから殺傷力があるのであって,普通の人間が同じようにパンチしても一発入魂でパンチするよりも返って与えるダメージが少なくなることは容易に想像できる.
まあ文字通り「無駄無駄無駄無駄無駄無駄…」になってしまうという事だ…(皮肉)
まとめ
今回は少々長々しい話になってしまったがまとめは次のようになる.
暗記科目教科は問題構造の層が少なくとてもシンプルな構成で自分の間違った部分を簡単に見つけられ,軌道修正しやすい.
数学には未到達の問題構造の層と言われる解答中に一切触れられることがない層があり,解答されることもなく未到達の状態で終わってしまうことが多い.
数学の問題は前半が分かったうえで後半へと話を進めていく問題形式が基本になるので,前半と後半で学習経験値に差が生まれ,知識の格差を非常に生みやすい.
数学が苦手だと感じる人はまずこの「未到達の問題構造の層」を1つずつ,1つずつシラミつぶしに知識として習得していかなければならない.
今回は以上になります.
次回は問題構造を踏まえて実際にどのように数学を勉強したらいいかの思考方法について話そうと思います.
ご愛読ありがとうございました.
