数学応用問題の解き方　～医学生の脳内を言語化します～

見たことのない問題に出くわすと、まったく歯がたたない！

クラストップの生徒は解けるのになぜ？

やっぱり数学はセンスな気がする。自分にはセンスがないんだ。

と、一度でも感じたことがある人が99％以上でしょう。私自身、「そもそも鉛筆が動かない問題」というものに何度も当たってきました。

しかし、「ちょっとしたこと」ができるようになってからは、初見の問題でも解けるようになりました。

ここでは、そんな「ちょっとしたこと」を紹介するとともに、国公立医学部に合格した私が、その数学の問題に対して「どのような」イメージを持って解いているのかを言語化していきます。

私は元々文系なので、センスと思われがちな数学を言語化することは得意です。読むだけ損はさせません。

ところで、中学数学と高校数学では難易度がまるで変わってしまうので、中学生向け編と高校生向け編に分けました。

さらに、例題で3年生で学ぶ範囲を選ぶと、そもそも分からない学生が増えてしまうので、1年生の単元から難問の例題を持ってきました。安心して読んでください。

あと、「無料範囲だけでも、私の考えていることは分かります。」高校数学でどう考えればいいのかを知りたい人だけ、有料記事を購入してみてください。

また、質問があればコメントしてください。対応可能です。

では、私の脳内を言語化していきます。

中学生向け

今回は、超難関中学入試を持ってきました。私が解くときに考えていることを全て書いていきます。

分からなかったら、とにかく代入してみること

「答えがどうなるのかサッパリ分からない！」なんて時は、「とにかく代入してみる」ことが近道だったりします。

これが今回扱う問題です。解きたい方もいるでしょうから、解説は少しスクロールしたところから始めます。

↓

↓

↓

では、私の解いていく過程を書いていきます。ところで、noteの形式上、数式を打ち込むことができません、、💦

数式の部分だけ、Wordで打ち込んだもののスクショを載せます。

戻るのは面倒くさいでしょうし、再掲します。

（1）から解いていきます。以後、カギ括弧が出たら、それは私の脳内で独り言している内容です。

ここで思考停止状態になり、手が止まる人が多い気がします。「とりあえず」何でも良いから、問題文からヒントを見つけて、メモしてみてください。何らかのヒントは得られます。脳内に戻ります。

これを前進とするかどうかはさておき、「とりあえず」何かを書いたことによって計算を始めることができました。

仮に、とりあえず書いたことが間違えていたら、計算に矛盾が生じるだけです。自分の仮説が間違えていたという事実もヒントになるので、ナイストライになります。脳内に戻ります。

ちなみに、高校数学の知識を使えば、まだ先の計算ができますが、中学生向けなので割愛。

ここまで来て、ようやく題名の「分からなかったら、とにかく代入してみること」を実行することになります。いきなり実行しろよ！と思うかもしれませんが、数学では、「どうして、その解法を思いつくに至ったのか？」が大切です。

いきなり、正しい解法を書くと、テキストの模範解答のように、なぜ、その解き方を思いついたのか分かりませんよね。

脳内に戻ります。

私は、問題を解くときに、実際このような独り言を脳内でしています。メリットはたくさんありますよ。例えば、今回なら、「あれ？マイナスが連続して出てきちゃったな。」ということです。脳内に戻ります。

困りましたね。解答の続きを次の章に書いていきます。すぐ下です。

素直な疑問をメモること

これは、どの数学の問題でも使えるテクニックです。「今感じていること」を素直に言語化してみると、解法が不思議と見えてくるんです。

前章の続きを考えていきます。

疑問に思ったことを、忘れないうちに言語化して、その疑問に自分なりのアンサーをしてみてください。今回の様に、疑問を否定できることでしょう。

そうすれば、解法が消去法で見えてきたり、新しい発想が芽生えたりします。

「分からない！分からない！」という状態の時、大概は、同じような3つぐらいの疑問が、熟考されることなく、頭の中をグルグル回っているだけです。1つずつ取り出して考えていきましょう。脳内に戻ります。

ここでも、ハードすぎるという素直な感想から、「何か合理的な探し方があるはず」という考えに至っている。とにかく、自分が感じたことを言語化して、それに答えていくこと。

ちなみに「折り返した」で私がイメージしたのは、反比例の表ですね。2つの数の組み合わせが、途中から入れ替わるだけになります。脳内に戻ります。

中学生でしたら、これくらいの説明ができれば十分です。（2）へ進みます。戻るのは面倒くさいので再掲します。

「いきなり6の約数って分からないよ！」と思うかもしれませんが、そんなの私も同じです。でも、6の倍数っていう答えを見たら、ハッとしましたよね？答えを聞いたら分かりましたよね？つまり、頑張れば自力で答えを出せるのです。

勉強が苦手な子は、答えを聞いても分からないんです。

知識はあるはずなのに、出てこない。これを改善する方法は、普段からクイズ番組を見たり、クイズ本などをやることで、自分の脳みそという本棚の隅に眠る知識を探す行程を何度も繰り返すことです。

こうして訓練することで、知識を引き出すのが上手になります。

ちなみにこれを中学入試で「互いに素」と言いますが、知らなくても大丈夫です。

「とりあえず」問題文をまねして変形させただけです。策があるわけではありませんが、こうやって、「とりあえず」何かをしている間に、問題が解けているんです。

私は問題文を見て、その場でパッと解けたことがありません。毎回こうやって、自分の感じたことを解決しているうちに解法が出てくるのです。

これで（2）お終いです。（3）いきましょう。

再掲します。

21まで割るのは、21までがよく使われる素因数だからです。

さて、調べた結果、2023＝7×17×17　でした。

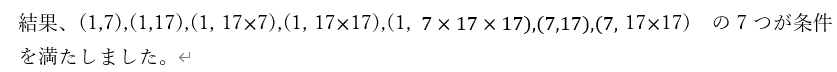
まとめ

応用問題を解くときの脳内を完全解説しました。特別なヒラメキがあるとか、直感が優れているとかっていうのは無いんです。

大切なのは、応用問題に直面したときに、「自分は今、どういう感情を持っているのだろうか？」ということをシッカリ言語化することです。

面倒くさいと感じたら、やり方にミスがありそうですし、数字が多すぎると感じたら、途中の計算過程を工夫する必要があるということです。

自分の感情を無視して「ええい、やってしまえ。」となる人が多いので、いったん自分の感情に素直になってみましょう。

そして、「とりあえず」何かを書き始めること。手が止まると思考も止まります。

高校生向け

前提

高校数学の応用問題は、基礎ができていないと手も足も出ません。しかし、その基礎を完成するのが大変なんですね。

今この記事を読んでいるあなたは、基礎問題精講レベルのものを完璧にできていますか？

できていないならば、応用問題の練習をするのは早すぎるので、基礎をシッカリ固めてから応用問題に取り組みましょう。

網羅系参考書の効率的な使い方をまとめた記事のリンクを貼ります。よければ読んでみてください。

前提はこれくらいにして、応用問題を解くためのアプローチを章立てしていきます。