マイナスかけるマイナスがプラスになること

最近、立て続けにおふたりの大人のかたが、私に算数・数学を教えてほしいとお申し出になりました。おふたりのかたに共通していたのは「学生時代に習った算数や数学は、受験テクニック的であった。もっと学問的に学び直したい」ということでした。そして、おふたりがたまたま共通しておっしゃった「なぞのこと」が、「マイナスの数とマイナスの数をかけるとプラスの数になること」でした。

マイナスの数は、中学に入ってすぐに習います。ちょうど今ごろ（きょうは２０２２年４月１８日です）、中学１年生は「負の数（マイナスの数）」を習うでしょう。そして、負の数も含めた足し算や引き算を習い、間もなく負の数も含めたかけ算や割り算を習い、その「負の数かける負の数が正の数になること」を学びます。以下に書きます通り、私はこのことを納得していますが、このことを納得できないかたが思いのほか多くいらっしゃることが、そのご質問からもうかがえますし、以下のような、私が中学生か高校生のころ読んだ、ある作家のかたの書いたエッセイからもわかります。（誰が書いたエッセイか、とか、詳しいことはすべて忘れています。覚えていることだけ書くことをおゆるしください。）

その作家さん（「作家」のことを「作家さん」という言いかたをすることに抵抗のある司書のかたに出会ったこともありますが、ここでは「作家さん」という言いかたをすることをおゆるしくださいね）がお書きになっていたのは「中学に入って、マイナスの数とマイナスの数をかけるとプラスの数になることを習った。しかし、私はそれがどうしても納得できず、そこで踏みとどまっているうち、数学から落ちこぼれてしまった」ということでした。私がそれをよく覚えている理由ははっきりしています。そこで踏みとどまるのが正しいありかたではないかと思ったからです。つまり、そのころから私はやはり「学問的」であったのです。要領がいい勉強法は、そこで踏みとどまらないことです。とにかくマイナスかけるマイナスはプラスであると（納得できるかどうかは置いておいて）了解して、先へ進むことです。しかし、それでは学問とは言えないのです。納得できないのに先へ進んではならない。その作家さんも「自分はマイナスかけるマイナスがプラスであることが理解できないほど賢くなかった。恥ずかしい」と言いたかったのではなく、おそらく「納得できないのに先へ進まねばならない理不尽さ」について書きたかったのであろうと思います。とにかく、それほどまでに「マイナスかけるマイナスがプラスになること」は納得しがたいことであるようです。

しかし、先ほども書きましたが、私は納得していますので、「なぜ多くの人が、マイナスかけるマイナスがプラスになることを納得できないのであろうか」ということを考えねばなりません。それを以下に考えます。たとえば、$${(-4)\times(-5)=20}$$です。$${-4}$$と$${-5}$$をかけると$${20}$$になるのです。これは、$${(-4)=(-1)\times4}$$であり$${(-5)=(-1)\times5}$$であることから$${(-4)\times(-5)=(-1)\times(-1)\times20}$$であり、結局$${(-1)\times(-1)=1}$$であることが納得できるかどうかにかかっていることになります。私がいま手元に持っている数研出版の検定外教科書である『体系数学１』は、これを、小学校からおなじみの「（道のり）＝（速さ）×（時間）」で説明しています。「道のり」や「時間」は正の数ですから、「道のり」を「位置」と言い換え、「時間」を「時刻」と言い換えています。つまり「西へ$${3}$$キロメートル進んだ」というのを「東へ$${-3}$$キロメートル進んだ」と言い換え、「$${1}$$時間前」というのを「$${-1}$$時間後」と言い換えて説明しているのです。東へ進むのを正の向きとし、時間が経過するのを正の向きとしますと、東へ時速$${-3}$$キロで走っていて、$${-1}$$時間後にどこにいるかと言いますと、それは西へ時速$${3}$$キロで走っていて、$${1}$$時間前にどこにいたかということですから、東へ$${3}$$キロメートルの地点にいたことになります。つまりプラス$${3}$$キロメートルだ！ということでマイナスかけるマイナスがプラスであることを納得してもらうことになっています。これでじゅうぶんの説明ですが、「なんかじょうずに丸め込まれたな」という気がしなくもないですね。それは「（道のり）＝（速さ）×（時間）」というものが、必ずしも納得させられたものではないからではないかと思います。では、以下のような例ではいかがでしょうか。

ウソのウソはホントですよね。ホントのホントはホントですけど。ここで「ウソ」がマイナス、「ホント」がプラスのつもりです。ウソのホントはウソであり、ホントのウソもウソです。マイナスかけるプラスはマイナスになるのです。あるいは、トランプを１枚持ってきていただきましょう。ウラのウラはオモテですよね。オモテのオモテはオモテですけど。こんなんでは説明になっていませんか？私の中でのイメージはこんな感じなのですけど…。あるいは「後ろを向いてバックしてください」。これは前進しませんか？

「お母さん、マイナス１０キロやせたのよ！」というのは「１０キロ太った」ことを意味します（この例はある中学の数学の先生が言っていたことから借りました）。こんな例ばかり習っていると、あたかも正の数と負の数は「リバーシブル」のような気がしてきますが、正の数と負の数で決定的に違うところがあります。正の数はかけ算について「閉じて」います。つまり正の数と正の数をかけても正の数になります。これに比べて負の数はかけ算について「閉じていない」わけです。負の数と負の数をかけると負の数にならない。「閉じている」は数学的に厳密な用語であり、こんなところで「雰囲気で」使ってはいけない言葉ですが、おそらくこれが多くの人の思う「マイナスの数とマイナスの数をかけるとプラスになるというなぞ」の原因であるように思われるわけです。「２乗して自分自身になる数はなんですか」と言われると、それは$${1}$$と$${0}$$であるわけです。$${-1}$$は２乗しても自分自身にはならず、$${1}$$になります。「２乗して自分自身になる数」が$${0}$$と$${1}$$だけであるのは、これが$${x}$$についての方程式$${x^2=x}$$の解だからですが、とにかくこれは$${1}$$と$${-1}$$の決定的に違う点だと言えます。

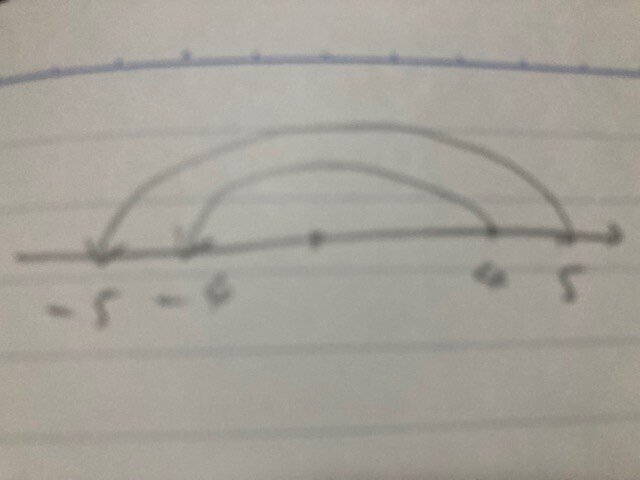
ところで、$${4}$$と$${5}$$はどちらが大きいでしょうか。$${5}$$ですね。では、$${-4}$$と$${-5}$$ではどちらが大きいでしょうか。これは$${-4}$$ですね。マイナスの符号をつけると、つまり２つの数に$${-1}$$をかけると、大小が逆になるのです。これは、高校に入って不等式を習うと、先生から「マイナスの数をかけたりマイナスの数で割ったりすると不等号の向きが変わることを忘れるな！」とくどく習うことになります。２つの数に同じ正の数をそれぞれかけても大小は変わりません。$${4}$$と$${5}$$の両方に正の数である$${2}$$をかけると$${8}$$と$${10}$$となり、$${10}$$のほうが大きいです。$${4}$$と$${5}$$のそれぞれに$${-2}$$をかけると$${-8}$$と$${-10}$$となり、$${-8}$$のほうが大きいです。それは$${-2=(-1)\times2}$$だからだと言えます。$${3}$$で割ることは$${\frac{1}{3}}$$をかけることと同じであり、やはり「２つの数に$${-1}$$をかけると大小が逆になる」ことがこの現象の本質であることがわかります。２００５年の就職活動のとき、ある私学で「不等式の両辺にマイナスの数をかけると不等号の向きが逆になることを生徒に説明するつもりで説明してください」という採用試験の面接での質問がありました。私は$${-1}$$をかけることが本質であることを言ったうえで「数直線の原点を指でおさまえて、数直線全体を『バッターン！』と180°回転させると、大小が逆になります」と言いました。$${-1}$$をかけることは、数直線を原点中心に180°回転させるのと同じことなのです。そして、それをすると２つの数の大小は逆になります。$${4}$$と$${5}$$で以下の絵を見てください。

同様に、$${2}$$と$${-1}$$の場合も見てください。$${-2}$$と$${1}$$になって、大小が逆になるでしょう。

同様に、$${-5}$$と$${-6}$$でも見てください。$${5}$$と$${6}$$になって、やはり大小が逆になるでしょう。

これは、その面接官の先生にはウケましたが、採用試験は落ちました。どのような理由かはわかりません。例のごとく、「生徒のほうを見ていなかった」ことかもしれません。大学院に戻って同輩にこの説明をしたときには納得してもらえました（当時はまだギリギリで大学院生でした）。教員になって最初の年、高校１年生が当たり、この「バッターン！」という説明をしたときには、日直だった佐々木くん（仮名）から日直の日誌に「『バッターン！』なんていらないし」という手厳しいご批判を受け、以来、やらなくなりました。その学校は典型的な三流進学校であり、「不本意入学者」が多いのでした。佐々木くんもそんな不本意入学者のひとりでありました。かわいそうに。ともかく、$${-1}$$をかけることは数直線を原点中心に180°回転させることと同じであり、これはつまり、$${-1}$$を２回かけると360°回転となってもとにもどることを意味しています。これもまた、$${-1}$$と$${-1}$$をかけると$${1}$$になることの説明ではないでしょうか。

ここから少し、複素数をご存知のかた向けの記述になります。虚数単位を$${i}$$としますと、これは$${i^2=-1}$$となる数でした。正の数を２乗すると正の数になり、負の数を２乗しても正の数になりますので、$${i}$$は正の数でも負の数でもなく、数直線上にありません。どこにあるかと言いますと、数直線を東が正の向き、西が負の向きになるように置いたとき、原点から北へ$${1}$$だけ進んだところに$${i}$$はあるのです。この平面を複素平面（複素数平面）と呼ぶことにしますと、$${i}$$をかけることは原点を中心に平面全体を90°回転させることになるのです。以下の絵をご参照ください。$${i}$$を２回かけると180°回転となって、$${-1}$$になることがご理解いただけますでしょうか。つまり$${i^2=-1}$$です。

そして、３回かけると$${-i}$$となって原点から南へ$${1}$$だけ進んだ点となり、４回かけると$${1}$$に戻ります。$${i^3=-i}$$で、$${i^4=1}$$です。以上で複素数をご存知のかた向けの記述は終わります。

といったわけで、私はマイナスかけるマイナスがプラスになることは納得しております。じつはこの記事を書く直接のきっかけは、あるnoteの記事を読んだことにあります。その記事は、おそらく大学の数学の先生が一般人向けに書いた本の紹介を出版社がしているものだと思われるものでした。冒頭で述べました通り、最近、私に数学を学びたいと申し出られたおふたりのかたがおふたりとも「マイナスとマイナスをかけるとプラスになる神秘」についておっしゃった通り、これは「常識と非常識の境目をねらった、うまい知識」なのでしょう。私は典型的な「非常識人」でありまして、そういう「授業の小ネタ」は持ち合わせていませんでした。多くの先生は数学に限らず「これを言うと生徒に『へえ！』って言ってもらえるのよ」という小ネタをたくさんたくわえており、そういうのを小出しにしながら「先生稼業」を務めておられるのでした。私には不可能なわざです。だから私は教員をやめさせられているのです。きょうのネタはおもしろかったですか？（ちょっとでもおもしろかったら遠慮なく「スキ」をおしてくださいね！私はそれで大きな勇気をもらえます！）それではまた！