
アインシュタイン(満26歳)のノーベル賞論文は穴だらけ - Part Nine
論文の第8節を解読していきましょう。
第7節の解読はこちら。そして以下が第8節です。

日本語にすると「固体の光照射による陰極線の発生について」です。またもや小難しい節タイトルです。
この第8節のメインテーマは、あるドイツの実験物理学者による、ある実験結果についてです。
ハインリヒ・レナードという実験家さんです。お師匠さんにあたるヘルツ教授が「440ヘルツ」のように物理単位にその名を残したのに対し、その愛弟子であるレナード先生は、特にこれといった名を残すことはありませんでした。
しかし彼が1902年に行った実験は、「光電効果」と呼ばれる謎めいた現象を突き止めた、科学史に残る一大業績と私は考えます。何よりアルベルトくんの、くだんの論文のクライマックスすなわち今回取り上げる第8節そして最終の第9節で、大きくフィーチャーされているのだから、不滅の業績といっていいと思います。

「わからへん」という皆様のお声が聞こえてくるようです。
もう少し直観的にわかる絵をお見せするとですね…
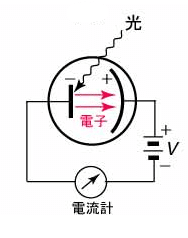
今度は多少伝わるのではないかなーと期待しているのですが、いかがでしょう?
「わからへん」
ああそうですか。要点をちゃちゃっとご説明します。電池の下側より、この電気回路のなかを、赤の矢印で示したように電子が移動していきます。

しかし見てのとおり、途中で道路が途切れていますね。そこで、紫外線を以下のように当てると…

なんと電子くんが、向こう側の崖まで、空中大ジャンプするのです!

そのおかげで、電池のマイナス極からプラス極まで、うまく電子くんが回ってくれるようになります。まさに回路ですね路を回っていくの。

崖から崖へ、たーっと勢いよく電子くんをジャンプさせているのが、光(というか紫外線)のエネルギーであることは間違いないとして、この実験を行ったレナード先生が精密に測定したところ、当てる紫外線の強さと、実際にジャンプする電子の総エネルギーが、必ずしも比例しないというのです。

この不思議を、アルくんは、絵にするとこんな風に説明できると、くだんの第8節で検証しています。

「hν」とあるのは、前回解説したところの「光量子」です。光のエネルギーの最小単位、すなわち光エネルギーのつぶ。パチンコ玉をイメージしてください。それが金属表面にあたると、この表面内部に詰まった電子くんが、はじき出されるわけです。「w」とあるのは、はじき出すにあたっての抵抗値みたいなものと、イメージしてください。ある値以上のエネルギーでないと、光量子は電子くんを金属表面よりはじき出せないのです。
そういう風に考えると、レナード先生が不思議がった不思議が、うまく説明できてしまうのです! 光の正体をめぐる、アルくんのこの洞察力、私が敬愛してやまないシャーロック・ホームズやその賢兄マイクロフト・ホームズをも凌ぐものがあります。

ただ、アルベルトはこの第8節でも、例の意地を張り通しています。

赤で括った等式ですけど、プランク教授に倣って「h」(今でいうプランク定数)を使えばもっとすっきりするのに、意地でも使わないで、代わりにこここでも「R/N・β」で押し通してくるのです。


ほかにもこの第8節をわかりにくくしている点があります。ここの記述。

日本語にしてみます。DeepL さんよろしく。「うんいいよ」
導き出された公式が正しければ、直交座標で励起光の周波数の関数として表されるIIは、分析される物質の性質に依存しない傾きを持つ直線でなければならない。
ここ、できればこんな風にグラフを挿んでほしかったです。

これを挿んで、こう啖呵を切っていれば、アルくんもっと早く理解者を得られたのではないでしょうか。「プランク教授は『光のエネルギーが粒状になるのは、光を放つ物質の性質上そうなっとるんやろう』と言うてはるが、わしの考えでいくと、物質の性質とは無関係に、こういう斜めの線が生じることになるから、つまりプランク説ではあかんねん。光はもともと粒状にしかエネルギーを持ちえないとみるべきや」と。

余談ですが、彼がこう喝破した1905年の暮れに、レナード教授はノーベル物理学賞を授与されています。その記念講演ではアインシュタインへの言及はいっさいありません。おそらくろくに目を通していなかったのでしょう。そもそもレナードの受賞理由は、この実験によって電子が空中を移動する「陰極線」を作ることを突き止めたことでした。アルくんによるその実験データの解釈は、当時としては前衛すぎて、たぶんレナードも(もしきちんと読んでいたとしても)理解できなかったであろうと想像します。

次回、最終節を取り上げます。第9節。わずか1ページです。頑張っていきましょう!
