
ポール・ディラックの原論文を読んでみよう(1928年:ディラック方程式)
今回取り上げるのは "The quantum theory of the electron"(電子の量子力学)。1928年2月1日付で刊行。これはニールス・ボーアを脱帽させ、パウリを思いっきり動揺させ、ハイゼンベルクをして「イギリスにひとり、絶対に勝てないど秀才がいる」といわしめたブツであります。
特殊相対論と量子力学は相性が良くないことで知られていました。それを後に「ディラック方程式」と呼ばれることになる数式を捻りだして、橋を架けてみせたのです。

橋? そうです、それもごく素朴な技。これです。

行列、それも縦横それぞれ2の、一番素朴な行列です。高校数学で習うレベルのごく易しい行列。
前年にクライン&ゴルドンの二人がこしらえた方程式は、解くと電子の存在確率が負になってしまう場合が生ずるという欠陥がありました。それを行列を使って克服したのが、ディラックの方程式です。
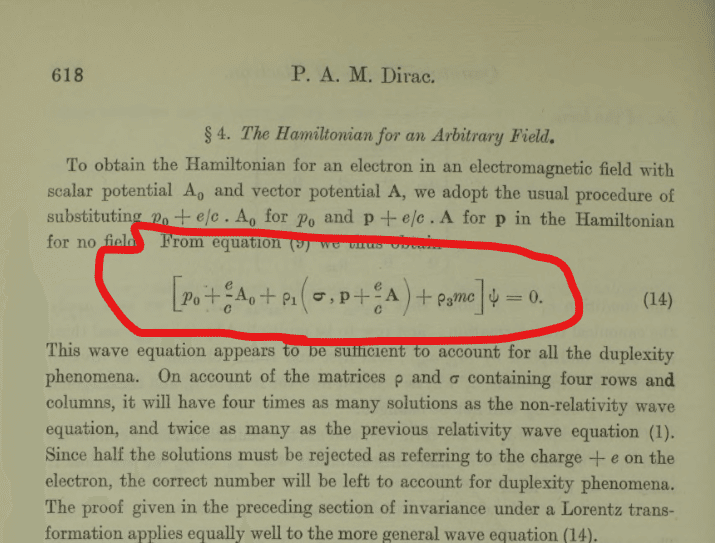
当時のヨーロッパの天才たちがどのくらい衝撃を受けたか、この原論文を読むと分かる気がします。
行列でもって難攻不落の要塞を落とすというこの技、元ネタがあります。前年(1927年)にパウリが、電子のスピンに右回りと左回りの二つがあることを説明するために行列を使った論文。これに触発されたのでは、といわれています。
パウリは電子スピンについてもともとは完全否定派で、しかしいろいろな研究によって否定できなくなったとき、鞍替えして、もともと行列力学派だったこともあってスピンの右回り/左回りについて行列で説明するという離れ業をみせて喝采されていました。以下はその1927年論文の英訳版です。

ドイツ語の原論文、検索したのですが購入しないと閲覧できないようですので泣く泣く上の英訳版を紹介します。

おおギョーレツ!

「それはモーレツやー!」 昭和な笑い、大好きですご容赦ください。ディラックはこの論文を(おそらくこの英訳で)読んでいて、それを自家薬籠中のものとして、

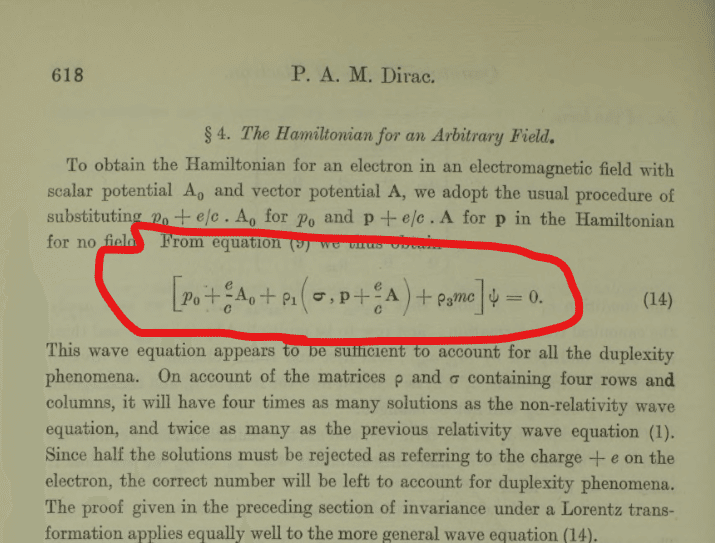
と大飛躍したものと思われます。
ちなみにこれには話の続きがあります。特殊相対論と整合するような方程式を導出するには、いうまでもなく特殊相対論の方程式「E=mc^2」が、この方程式の導出にあたって使われているわけですが、後の研究で、この相対論方程式を使わなくてもディラック方程式は導出できることが判明しています。
晩年のディラックも、そのことに薄々気づいていたようです。この点については数学の形式面からの議論となるのでここでは省きます。
そうそうこの論文には続編があります。後日また取り上げる機会もあるかもしれないので紹介しておきます。
