
エントロピーについて彼はどう考えていったか?
アインシュタインの論文を、最初期つまりアマチュアの頃より順に目を通してきました。
そうしていくうちに、気になることが気になるようになっていく気が私の中でわいてきました。
エントロピーについて、です。
ギリシャ語の「移りゆくもの」(トロピー)に、ドイツ語の「そこに向かっていく」(エン)をくっつけて造語されたのが「entropie」だそうです。1865年に、ドイツの物理学者クラウジウスが命名しました。

この方の論文は、当時より「難解」「なにゆうてんのかわからへん」と言われてきました。それもそのはず、彼の熱学研究は、とある人物の半ばオカルトめいた説を出発点にしていたからです。
オカルト? そうです。いまでいう「エネルギー」の概念の、当時とりわけ根拠不明なものを、です。1850年前後に、三人の学者がほとんど同時に「エネルギー」の考え方を言い出していましたが、そのなかでとりわけニューエイジ臭さく裂な方がいらっしゃって、当時の物理学者たちを戸惑わせていました。クラウジウス先生はというと、この方の根拠不明な数式に着目して、論文中ではそれに言及しないよう、まわりくどい論じ方を長々としながら、最終的には11年がかりで「エントロピー」を命名したのでした。
ちなみに高度に数学的な議論の末に、彼は「エントロピー」の考え方にたどり着きました。高度といっても普通の微積ですけどね。ただ抽象的な議論の積み重ねで、数式から数式を繰り出していって、そしてこう言い切ったのです。「エネルギーは保存するけれどエントロピーはだんだん増えていく」と。
前に私はアインシュタイン論のなかで、物理宇宙は「エネルギー」と「エントロピー」の二つのメーターでバランスを取っている、回っていると述べました。
この事実に気づいた世界で最初の方が、かのクラウジウス教授でした。
とはいうもの彼のこの気づきは、あくまで気体についてでした。今でこそ小学校の理科実験室での化学反応から宇宙の果てのブラックホールまで、この二つのメーターで語られているけれど、19世紀後半の後半までは、エントロピーの主戦場は気体について、でした。
*
液体でも固体でもなく、気体の研究にヨーロッパの科学者たちが熱をあげたのには、訳があります。
18世紀後半より蒸気機関がイギリスで発達していました。そのおかげで蒸気についてのデータがかなり前より揃っていました。気体全般についても蒸気の性質が当てはまるんじゃないか…当時のヨーロッパの科学者たちがそんな風に想像を広げていったのは自然ないきさつでした。
そういうわけで「理想気体」と呼ばれる、実際の気体と地続きなんだけど限りなく仮想的な気体をイメージして、それを微積を駆使して議論していくスタイルが確立していました。
このやり方は、精密さを増せば増すほど、間違った説を煽る結果となりました。詳細は語ると長くなるので手短にいうと「熱素」という架空概念が定説化していまったのです。目に見えないほど小さな「熱素」と呼ばれる物質があって、たとえば金属に触れてひやっとするのは指先から「熱素」が金属に高速移動するからである…そんな風に理解されていたのです。
微積は「無限小」を扱う数学ですので、それを駆使した科学理論それも人間の視覚ではとても認識できないほど微細な世界についての科学理論を、微積で探求すると、「熱素」のような微細粒子をどうしても(無意識に)想定してしまうのです。いいですか無意識にです。
ここが落とし穴なんじゃないかと気づくひとも、いたことはいたようですが、より精緻な実験データが揃ってきて「熱素」の存在を否定せざるをえなくなってからも、取って代わる新説を科学者たちはうちだせないまま、あーだこーだと互いの説の弱点をつつき合っていました。
そこのあたりの水掛け論的なあーだこーだについては、例によって語りだすと長くなってしまうので省きますが、クラウジウス先生は、出発点こそ当時の少々ニューエイジな仮説でしたが慎重かつ晦渋な議論と数式の積み重ねによって、とうとうすっきりした新説を打ち立てたのです。「エネルギー」と「エントロピー」の二本柱でこそ、熱について語れるぞと。
どのくらいすっきりしていたかというと、今ではそれぞれ「熱力学の第一法則」「第二法則」として、物理と化学の両方の教科書に、大きく記されているくらい、すっきりしたものでした。(ちなみに高校ではなく大学の教科書に、です)

さあて一方この19世紀後半、熱の研究において、もうひとつ前衛的な理論が形になりつつりました。
「気体分子運動論」ってことばを、高校の化学で目にしませんでしたか。あれです。あれが19世紀半ばよりぐんぐん発育していったのです。


この「気体分子運動論」に「エネルギー論」をふりかけて、微積と対数関数をブレンドした杖を一振りすると、あーら不思議、分子の種類がすべて同じと仮定した場合、どのくらいの割合の分子がどのくらいの熱エネルギーを担って、それぞれどのくらい暴れまわって気体全体の圧力つまり「気圧」を作り出すかを、算出できてしまうのです!
この鮮やかさは当時の若手物理学者たちに強烈な印象を残したようです。そのひとりがボルツマンでした。
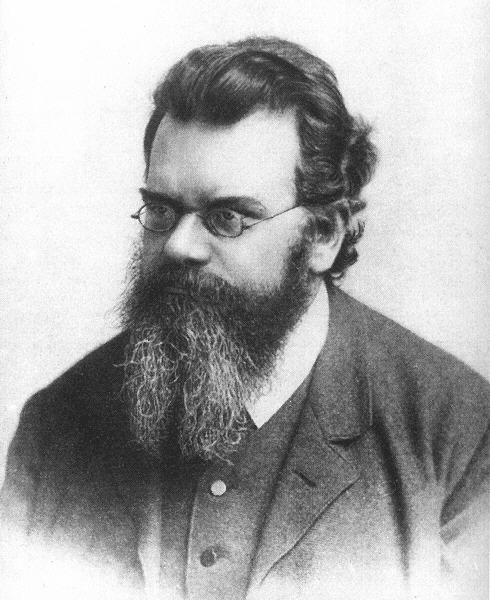
さらに上をいってみせるぜ!と微積と対数関数をブレンドしてバージョンアップした杖を作って、一振りすると、あーら不思議、分子の種類がまちまちでも、同種の計算ができてしまいました。
いわゆる「ボルツマン方程式」(1872年)。

非線形微分積分方程式(そう「非・線形」!)なので解くのが大変。実際これの解き方が編み出されるのはたしか1917年でしたが、とにかく気体分子運動論をひとつの数式に落とし込むことに、ボルツマンは成功したのです。1872年のことでした。
さらに5年後、彼はもっとすんごい数式を捻りだしました。これです。

前にお見せしましたね、ボルツマンのお墓(というか像)です。彼の頭上に彫り込まれた…

ここにある「S」は「エントロピー」のことです。「W」は…めんどくさいので、気体分子がある箱のなかで群れているときの群れパターンと思っておいてください。パチンコ玉がパチンコ台(それも昔の型の)をがちゃがちゃがちゃーと群れなしてはじけまくっている様を思い浮かべられる方は思い浮かべてくだされば、感じは思い浮かべられると思います。
この「S」については、すでにクラウジウス教授が数式化していましたが、あれは微積計算の式としてでした。
一方で、彼より若輩にして最大のライヴァルに成長したボルツマンは、気体分子運動つまり無数のパチンコ玉がパチンコ台をがしゃがしゃがしゃーとはじけていく様より「S」の式を導出したのです。
しかし!(このフレーズが頻出しますが大目に見てやってください) ボルツマンは実は以下の「k」は式に使ってはいませんでした。
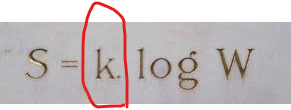
これをボルツマンの式に挿むようになったのは、最終的には後世の天才・アインシュタインによるものでした。
細かい話は例によってとばしますが、クラウジウスとボルツマンは、二人とも気体を前提にしてエントロピーについて議論していました。
ところがその頃、クラウジウスの教え子のひとりが「エントロピーの考え方を気体以外に応用できる」と言い出したのです。
ボルツマン方程式(1872年)についてはすでに触れたとおりですが…

これの1年後に、クラウジウスの教え子のひとり・ホルストマンが、化学反応を説明するのに「S」が使えるとする論文を世に問いました(1873年)。これが画期的な内容でした。実は4年前に彼はすでに熱化学とでもいうべきニュー・フィールドの論文を世に出していました。1873年のものはそれよりぐっと洗練されたものです。
無数のパチンコ玉の群れパターンの数が「S」だとする、ボルツマンの主張は直観的にわかりやすいものでしたが、それとほぼ時を同じくして、ボルツマンの先行者にしてライヴァルでもあったクラウジウスの、教え子のひとりであるホルストマンが、パチンコ玉イメージに寄らない「S」の理解と化学方面での活用法を形にしていた事実は、科学史的にみても非常に興味深いものを感じますね。

この二つの流れが、1902年にギブズとアインシュタインがそれぞれ独自に整理され、さらに翌1903年にはアインシュタインによって「S」のより普遍的な解釈に統合されていくのです。
*
ふう。アインシュタインの研究を追った文献はいろいろあります。それぞれとても面白く読ませていただきました。しかしこうしてご本人の原論文にくわえ、彼に直接間接に影響を及ぼした方々の研究について遡って追っていくと、これまでのアルベルト研究でぽっかり空白になっているものに気づかされます。
それがどういうものなのか、今のところ私もうまく絵が描けないでいます。

