【統計力学７】ボルツマンの式【エントロピーとの関係】

今回は分配関数と状態数の関係を探り，実はそれが熱力学の自由エネルギーとエントロピーとの関係と密接に結びついていることを見ます．有名なボルツマンの式が得られ，エントロピーの統計力学的な解釈を与えてくれます．

前回得られた統計力学の基本公式によれば，マシュー関数は

$$
\mathcal{F}(B,V,N) \sim k\ln Z(B,V,N)
$$

と書かれますから，逆に分配関数は

$$
Z(B,V,N) \approx e^{\mathcal{F}(B,V,N)/k}
$$

と書くこともできます．よって，カノニカル分布は

$$
\begin{align*}
f(q,p) &\approx e^{-\beta H(q,p) - \mathcal{F}(B,V,N)/k}\\
&= e^{-(B H(q,p) + \mathcal{F}(B,V,N))/k}
\end{align*}
$$

と書くこともできます．

ボルツマンの式

着目系が平衡状態にある（または孤立していると考えてもよいです）ときは，エネルギーはある決まったマクロな値

$$
H(q,p) = E(B,V,N)
$$

を持つとしてよいので，この場合，カノニカル分布は

$$
f(q,p) \approx e^{-(B E(B,V,N) + \mathcal{F}(B,V,N))/k}
$$

と書けますが，決まったエネルギーを持つ系についてはミクロカノニカル分布

$$
f(q,p) =\frac{1}{W(E,V,N)}
$$

で書くこともできるはずです．

カノニカル分布とミクロカノニカル分布が一致してほしいので，

$$
B E(B,V,N) + \mathcal{F}(B,V,N) \sim k\ln W(E,V,N)
$$

が成り立ちます．ギブズ・ヘルムホルツの式

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\pd{\mathcal{F}(B,X)}{B} = -E(B,X)
$$

が平衡状態では成り立つので，「ギブズ・ヘルムホルツの式を満たすようなエネルギーの値」で左辺の変数を逆温度からエネルギーに取り替えると，左辺はちょうど熱力学ポテンシャルとしてのエントロピーになりますから（この記事を参照），

$$
S(E,V,N) \sim k\ln W(E,V,N)
$$

であるべしとわかります．熱力学的重率は状態数を用いてもよいので

$$
S(E,V,N) \sim k\ln \Omega_0(E,V,N)
$$

としてもよい．エントロピーが状態数の対数に対応するという関係が得られました．
これらの式はボルツマン（Boltzmann）の式と呼ばれます．状態数はあるエネルギーのもとでとりうるミクロ状態の数ですから，エントロピーは「可能性の広さ」を表していると言えます．

（注: 体積が大きいほど状態数は大きくなることから，粒子が一か所に集まっているよりもバラバラになっている状態のほうが状態数が大きく，エントロピーが大きくなります．そのような状態は乱雑な状態に見えることから，エントロピーを「乱雑さ」と表現するのをよく見かけます．しかし，エントロピーはエネルギーが高くても大きくなります．エネルギーが高ければ，各部分にエネルギーを分配する仕方の可能性は広がりますが，このときの「乱雑さ」とはいったい何のことでしょうか．「乱雑さ」は「可能性の広さ」の一つの側面に過ぎないと私は思います．（そもそも乱雑さという言葉は曖昧なので，どう定義するかも問題だと思います．））

ギブズのパラドックスについて

エントロピーは示量変数です．そのため熱力学的に正しい結果を与えるためには，状態数は

$$
\newcommand{\lr}[1]{\left(#1\right)}
\newcommand{\explr}[1]{\exp\left(#1\right)}
\Omega_0 \approx \explr{N \sigma\lr{\frac{E}{N}, \frac{V}{N}}}
$$

のように密度の関数$${\sigma(E/N, V/N)}$$を用いて書けなければなりません．実は，これを満たすために，理想気体の状態数を数える際には粒子数の階乗のファクターで割っていたのです（こちらの記事参照）．粒子数の階乗のファクターで割らないとエントロピーの示量性が再現されないことはギブズのパラドックスと言われ，不思議に思われていました．しかしこれは単に自然界が同種の粒子を区別していないことを物語る一つの表れだと思われます．ちなみに量子力学に基づいて統計力学を組み立てれば，このようなミステリーは初めから起こらないようになっています．

分配関数と状態密度の関係

分配関数が単なる規格化定数でないことは，分配関数の定義式を

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\frac{dqdp}{h^f} = dE \pd{\Omega_0}{E} = dE \Omega(E)
$$

なる関係を使い，エネルギーの積分の形に書き換えて

$$
Z(\beta) = \int dH(q,p)\ \Omega(H(q,p)) e^{-\beta H(q, p)}
$$

と書くと，ちょうど分配関数は状態密度のラプラス（Laplace）変換になっていることからも察せられます．

この形に実用性は特にありませんが，ミクロカノニカル分布で活躍する状態数とカノニカル分布で活躍する分配関数との結びつきを見ることができます．

（注: もしも確率論や統計学になじみがあるなら，状態密度を状態の分布関数と思えば，分配関数は「エネルギーを確率変数とする特性関数のようなもの」（ただしフーリエ変換でなくラプラス変換なので，エネルギーが高いところの分布を減衰させています）なのだと理解できるかと思います．また，特性関数の対数はキュムラント母関数と呼ばれますが，マシュー関数がキュムラント母関数に対応します．キュムラント母関数の微分によって，あらゆる次数のキュムラントが求まりますから，マシュー関数の微分からはエネルギーの期待値（一次のキュムラント）やエネルギーの分散（二次のキュムラント）が求まるという形になります．）

上の式を部分積分してから，積分の中身を指数にまとめると

$$
\begin{align*}
Z(\beta) &= \beta \int dH\ \Omega_0(H(q,p)) e^{-\beta H(q,p)}\\
&= \beta \int dH\ e^{\ln \Omega_0(H(q,p)) -\beta H(q,p)}
\end{align*}
$$

となります．（部分積分しなくてもよいのですが状態密度でなく状態数で書きたかったので部分積分をしました．状態数なら無次元なので対数をとる罪悪感がなくなります．）

最大項での近似

上式で指数の肩の関数のオーダーが$${\ln \Omega_0(H(q,p)) -\beta H(q,p) = O(N)}$$と粒子数のオーダーなことから，熱力学極限では，上式で積分される指数関数はエネルギーについて激しく変化する関数です．したがって，熱力学極限では積分の値を，指数関数の肩にある関数が最大値をとるときで置き換えることが十分良い近似となります．以前にカノニカル分布とミクロカノニカル分布が一致する理由について説明したときと同じ議論です．

最大値をとるようなエネルギーの値は，極値を与える条件から，

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\pd{\ln\Omega_0}{H} = \beta
$$

を満たすようなエネルギーです．このエネルギーの値を

$$
H(q,p) = E
$$

と置けば，最大項での近似により

$$
Z(\beta) \approx e^{\ln \Omega_0(E) -\beta E}
$$

とすることができます．

（注: もう少しちゃんとした評価をするなら，マシュー関数を「最大値を与えるエネルギーからのずれ」の二次までテイラー展開します．0次の項は積分の外に出せ，一次の項は微分係数が０になって出てこないので，二次の項だけガウス（Gauss）積分を使って計算します．しかしこれは単に式の次元をキャンセルしてくれる以外に大した意味はないですから，あまりちゃんとやる価値はないかなと思います．）

対数をとれば，

$$
\ln Z(\beta) \sim \ln \Omega_0(E) -\beta E
$$

となります．

この式は，状態数の対数をルジャンドル変換すると分配関数の対数が得られることを示しています．熱力学との対応を思い出せば，これはエントロピーからマシュー関数へのルジャンドル変換にほかなりません．

一般化マシュー関数を

$$
\mathcal{F}(H(q,p)) = \ln \Omega_0(H(q,p)) -\beta H(q,p)
$$

で定義すれば，一般化マシュー関数を最大にするようなエネルギーが平衡状態として実現するわけです．
これは熱力学の自由エネルギー最小の原理に統計力学的な解釈を与えていると考えられます．一般化マシュー関数を最大にするために，統計力学的なエントロピーをできるだけ大きく，かつエネルギーをできるだけ小さくするような内部変数（代表点）が実現することがわかります．

（注: もちろん，時間に伴って平衡状態に移行すること（緩和）の説明は含んでいません．平衡統計力学でも緩和は前提として用いています．）

また，分配関数を逆ラプラス変換して，同様に極大を与えるような温度で積分される関数を置き換えて近似すると，ちょうど今の逆で，マシュー関数からエントロピーへのルジャンドル変換を与えます．これには逆ラプラス変換の知識が必要なので，これ以上論じるのはやめておきます．しかし，このように，熱力学でルジャンドル変換で結ばれる関係は，統計力学のレベルではラプラス変換で結ばれていることは大切だと思います．

（余談: 実は，スターリングの公式も最大項で近似する方法で導けます．ガンマ関数の定義

$$
\Gamma(x) = \int_0^{\infty} dt\ e^{-t} t^{x-1}
$$

に対して最大項で近似する方法を使ってみてください．）

今回のまとめ

・ボルツマンの式

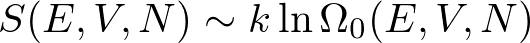
はエントロピーに「可能性の広さ」という解釈を与える．

・統計力学的なエントロピーをできるだけ大きく，かつエネルギーをできるだけ小さくするような内部変数が平衡状態として実現する．これは自由エネルギー最小の原理にほかならない．

・熱力学でルジャンドル変換で結ばれる関係は，統計力学のレベルではラプラス変換で結ばれている．