【流体力学ミニマル・後編】流体の運動【ナビエ・ストークス方程式】

物理量の時間変化を記述したいとき，オイラーの方法ではどのように記述すればよいのかが問題となります．そこではバランス方程式が数学的に主要な役割をします．（前編はこちら．）

２．バランス方程式

ある時刻において空間にある物理量が分布しているとします．これを$${F(x,t)}$$と書きます．空間に固定された体積の中のその量の全量を考えるには，物理量を体積にわたって積分すればよろしい．その時間変化は，体積の表面から出入りしている量と，体積中に湧き出す量に注目すれば追うことができます．表面から単位時間あたりに流れ出る量を向きも含めて$${\bm{V}(\bm{x},t)}$$とすると，面積要素$${dS}$$を通って単位時間に流れだす量（流量）は

$$
\newcommand{\Sur}{\bm{S}}
\bm{V}\cdot d\Sur
$$

と書けます．ただし，$${\bm{n}}$$を面積要素（表面上の微小な面積）$${dS}$$に垂直な単位ベクトルとして，太字の$${d\bm{S}}$$を

$$
d\bm{S} = \bm{n}dS
$$

と定義しています（図も参照）．

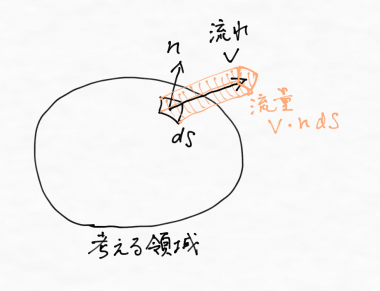
これを面積分したもの（表面での出入り）が全量の変化量に等しいはずなので，

$$
\frac{d}{dt} \int_V d\bm{x} \ F(x,t) = -\int_S \bm{V}(x,t)\cdot d\bm{S} + \text{体積内で湧き出した全量}
$$

という等式で結ばれます．この式をバランス方程式の積分形と呼ぶことにします．ただし，上式において，右辺第二項には単位時間当たり湧き出した量も考慮してそれも加えています．また，積分の範囲については

$$
\int_V: \text{考えている体積 }V\text{ 全体についての積分}\\
\int_S: \text{考えている体積 }V\text{ の表面 }S\text{ 上での積分}
$$

を意味しています．そして，いま，

$$
\text{体積内での湧き出しの全量}= \int_V d\bm{x}\ q(\bm{x},t)
$$

というふうに，ある点での湧き出し量$${q(\bm{x},t)}$$を用いて書けるとします．

バランス方程式の積分形の左辺の微分と積分を入れ替え，右辺にはガウスの発散定理を用いれば上の式は

$$
\newcommand{\Div}{\mathrm{div}\,}
\newcommand{\x}{\bm{x}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\int_V d\x\ \pd{F(x,t)}{t} = -\int_V d\x \ (\Div \bm{V}(x,t) - q(\x,t))
$$

と変形できます．（ガウスの発散定理を用いると，面積分は体積積分に書き直されます．表面での物理量の出入りを，体積内の微小部分での出入り（発散）の和をとることによって置き換えるようなイメージの定理です．）体積は任意なので

$$
\newcommand{\Div}{\mathrm{div}\,}
\newcommand{\x}{\bm{x}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\pd{F(x,t)}{t} = -\Div \bm{V}(\x,t) + q(\x,t)
$$

を得ます．これをバランス方程式といいます．

質量のバランス

バランス方程式だけでは一般的すぎて物理法則ではありません．ここに物理を入れていきましょう．考えている物理量が密度の分布$${\rho(\bm{x},t)}$$の場合，どこからともなく湧き出すことはないという物理的な条件（質量保存則）を入れることができます．流れ出る量（質量流量）は

$$
\rho(\bm{x},t)\bm{v}(\bm{x},t) \cdot d\bm{S}
$$

なので，バランス方程式は

$$
\newcommand{\Div}{\mathrm{div}\,}
\newcommand{\x}{\bm{x}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\pd{\rho(\x,t)}{t} = -\Div (\rho(\x,t)\bm{v}(\x,t))
$$

となります．これを特に連続の式といいます．

圧縮性・非圧縮性

流体が非圧縮性（つまり縮まない）なら，

$$
\rho = \text{const}
$$

なので，

$$
\newcommand{\Div}{\mathrm{div}\,}
\Div \bm{v} = 0
$$

が得られます．これを非圧縮性の定義と思ってもよい．

圧縮性の流体の取り扱いは数学的にかなり難しいので，流体を非圧縮性と近似する扱いをよくします．ふつうは密度変化は小さいのでこのような理論でもよいのですが，気象学のように高度差によって気圧が変わり密度が変化するような場合，音速に比べられるくらい流体の運動の速い場合，音波のように速度場の変化が速い場合などでは圧縮性を考慮する必要が出てきます．

流体の代表的な速さ$${U}$$と音速$${c}$$の比

$$
M = \frac{U}{c}
$$

をマッハ（Mach）数と呼びます．マッハ数が0.3のとき，約5パーセントの圧縮が起こります．これより小さいときは，経験的に非圧縮性と近似してよいとされています．

３．流体に加わる力

流体が加速運動するのは力がかかった結果と考えられます．というわけでここでようやく力を考えましょう．

流体の小部分に働く力には体積に比例するような力があります．たとえば，重力がそれです．
このほかに，微小部分は，その表面を通してとなりの要素から何らかの力を受けるでしょう．この力を記述するのが応力（stress）です．ただし，力は面積に比例するので，応力は面積当たりの力で定義します．

応力テンソル

ある位置を通るひとつの面を考えます．その面の単位法線ベクトルを

$$
\bm{n} = \begin{pmatrix}
n_x\\
n_y\\
n_z
\end{pmatrix}
$$

とします．

静止している流体や，粘性のない流体なら，この面を通して垂直に力を及ぼしあいます．この単位面積当たりの力を圧力といいます．すなわち，圧力は法線ベクトルに平行な向きに働きます．一方，粘性があって運動している場合には，一方の側がもう一方の側を引きずるような面力（せん断応力）も微小部分同士に働きます．

応力は一般に，考えている面に垂直でないばかりか，考える位置や面の向きを変えると大きさや向きが変わります．よって，応力を，位置$${\bm{x}}$$と面の向き$${\bm{n}}$$によって定まる３つの成分を持つベクトルとして

$$
\newcommand{\x}{\bm{x}}
\newcommand{\n}{\bm{n}}
\newcommand{\T}{\bm{T}}
\T(\x,\n)
$$

と書くことにします．これは応力「ベクトル」です．

それでは，流体内部のある点に働いている応力を完全に記述するには，考えうる面のすべての方向について指定しなければならないのでしょうか．もしそうだとすると途方もなく困難に思われます．しかし，物理量というのは現象に内在する属性を表現するものであるはずで、それは現象のみから一意に定まるべきと思われます．人為的に選んだ面の向きに物理的な意味があっては困ります．

実は，応力と法線ベクトルとの間には簡単な線形関係式が成り立つので，その関係さえわかればよい，ということになります．
先にその結果だけを書くと，

$$
\newcommand{\x}{\bm{x}}
\newcommand{\n}{\bm{n}}
\newcommand{\T}{\bm{T}}
\begin{align*}
T_i(\x,\n) &= \sum_{j=x,y,z} T_{ij} (x) n_j \\
&=\begin{pmatrix}
T_{xx}(\bm{x}) & T_{xy}(\bm{x}) & T_{xz}(\bm{x})\\
T_{yx}(\bm{x}) & T_{yy}(\bm{x}) & T_{yz}(\bm{x})\\
T_{zx}(\bm{x}) & T_{zy}(\bm{x}) & T_{zz}(\bm{x})
\end{pmatrix}
\n
\end{align*}
$$

と書けます．右辺に現れたこの$${3\times 3}$$行列$${T_{ij}}$$のことを応力テンソルと呼びます．すなわち，ある点に働く近接力は９つの量によって表現できることになります．応力テンソルの対角成分を法線応力，非対角成分をせん断応力といいます．テンソルというのはベクトル間の変換をするものであって，しかもこのように現象に内在する物理量として現れるので，面のとり方の任意性が排除されています．

（ちなみにテンソル（tensor）の語源は応力の一種である張力（tension）から来ています．テンソルは数学的に一般化されていますが，もともとは応力を考えるところから生まれた概念なので，テンソルを理解するのには応力が最もわかりやすいと思います．）

それでは上の線形関係式を証明しましょう．

下図のような小さな四面体を考え，斜線部分に働く応力を考えたいとします．

次のように文字を定義します．

$$
\begin{align*}
\bm{n}&: \text{斜線部の面を指定する単位法線ベクトル}\\
e_x,e_y,e_z&: \text{各座標軸方向の単位ベクトル}\\
dS&:\text{斜線部の面積}\\
dS_x,dS_y,dS_z&:\text{各座標軸に垂直な直角三角形の面積}\\
dV&:\text{四面体の体積}
\end{align*}
$$

ニュートンの第二法則（質量 $${\times}$$ 加速度（$${\bm{a}}$$） $${=}$$ 力）から，

$$
\rho\ dV\ \bm{a} = \bm{T}(\bm{x},n) dS + \sum_{i=x,y,z} \bm{T}(\bm{x},e_i) dS_i + \bm{F}(\bm{x}) dV
$$

と書けます（右辺第三項の$${\bm{F} dV}$$は重力のような体積に比例する外力です）．ここで，体積を無限小にとる極限を考えると，体積のかかった項は面積のかかった項に比べて無視できることになって，

$$
\bm{T}(\bm{x},n) = - \sum_{i=x,y,z} \bm{T}(\bm{x},e_i) \frac{dS_i}{dS}
$$

と書けます．つまり，応力だけの和が釣り合っていなくてはなりません．（この結論はニュートンの第二法則から出発して得られていることから，運動している流体についても成り立つことに注意しましょう．）

ここで，簡単な図形的な考察をすると，斜線部分の面積と各軸に垂直な面の面積との比に

$$
\frac{dS_i}{dS} = n_i \ \ (i = x,y,z)
$$

という関係が成り立っていることがわかるので，上式は

$$
\begin{align*}
\bm{T}(\bm{x},n) &= - \sum_{i=x,y,z} \bm{T}(\bm{x},e_i) n_i\\
&= \sum_{i = x,y,z} \bm{T}(\bm{x},-e_i) n_i
\end{align*}
$$

とできます．二行目に行くために作用反作用の法則を使っています．さて，これを眺めると，勝手な向きを向いた面に働く応力は，常に各軸に垂直な面に働く応力に分解できる，ということに気付きます．こうして，求めたかった線形関係式が得られました．

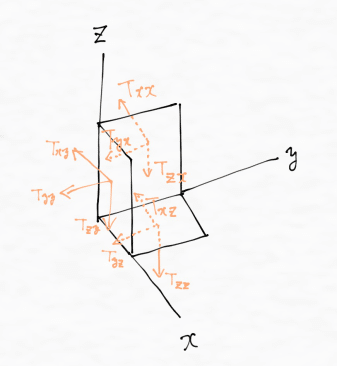
上式の右辺に現れた，各軸に垂直な面に働く応力を成分ごとに

$$
T_i (\bm{x},-e_j) = T_{ij}(\bm{x})\ \ (i,j = x,y,z)
$$

と置くと，これが応力テンソルの各成分に対応しています．添え字の一番目は応力の成分を表していて，添え字の二番目は応力の働く面を表しています．応力テンソルの各成分を図に書き込むと次のようになります．

圧力

静止流体ではどの向きの面を選んでもその面に垂直に同じ力が働くので，静止流体の応力テンソルは

$$
T =
\begin{pmatrix}
-p & 0 & 0\\
0 & -p & 0\\
0 & 0 & -p
\end{pmatrix}
$$

と対角成分のみになります．この対角成分の符号を変えたもの$${p}$$を圧力といいます．マイナスがついているのは，応力は引っ張る方向を正，圧力は押す方向を正と考えているからです．

応力テンソルの対角成分の和（トレース）を

$$
\mathrm{Tr}( T) = T_{xx} + T_{yy} + T_{zz}
$$

と書きます．テンソルのトレースは座標の回転に対して不変であるという性質があります（トレースは固有値の和であることが示せ，固有値はスカラーだからこれがいえます）．そこで，対角成分の平均値

$$
p = - \frac{1}{3} \mathrm{Tr}(T)
$$

を，流体が運動している場合にも拡張して圧力とみなすことにします．

応力テンソルを等方的な圧力の部分と，そこからのずれの部分に分解して

$$
\newcommand{\mcomp}[1]{\begin{pmatrix}
#1_{xx} & #1_{xy} & #1_{xz}\\
#1_{yx} & #1_{yy} & #1_{yz} \\
#1_{zx} & #1_{zy} & #1_{zz}
\end{pmatrix}}
T = \begin{pmatrix}
-p & 0 & 0\\
0 & -p & 0\\
0 & 0 & -p
\end{pmatrix}
+\mcomp{\tau}
$$

と書くことにします．この第二項のずれの部分は粘性と関係がありそうなので，それを次で考えます．さしあたってこのずれの項を粘性応力と名付けておきます．粘性応力のトレースは０であることに注意しましょう．

粘性

流体を特徴づける性質として，粘性（viscosity）があります．粘性とは，流体を変形させるときに，ひずみ速度に応じた力が必要となる性質です．

応力とひずみ速度の間に関係があることが現象論的に知られています．流体に特別な方向性がないとすれば，応力は単なる圧力のほかに，ひずみ速度に比例する項を持つと仮定できます．（これはちょうど弾性体に対するフック（Hooke）の法則の，流れバージョンのような仮定です．）この仮定が成り立つような流体のことをニュートン（Newton）流体といいます．
すなわち，ニュートン流体では

$$
\newcommand{\identity}{\begin{pmatrix}
1 & 0 & 0\\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}}
\newcommand{\mcomp}[1]{\begin{pmatrix}
#1_{xx} & #1_{xy} & #1_{xz}\\
#1_{yx} & #1_{yy} & #1_{yz} \\
#1_{zx} & #1_{zy} & #1_{zz}
\end{pmatrix}}
\mcomp{\tau}
=\mu \mcomp{\dot{\gamma}}
-\frac{\mu }{3} (\dot\gamma_{xx} + \dot\gamma_{yy}+ \dot\gamma_{zz})
$$

が成り立ちます．ここで出てきた比例係数を粘性係数といいます．第二項はトレースが０になるために必要ですが，非圧縮性なら，

$$
\dot\gamma_{xx} + \dot\gamma_{yy}+ \dot\gamma_{zz} = \mathrm{div}\, \bm{v} = 0
$$

なので消えます．

４．運動量のバランス（運動方程式）

考える体積内の物理量として運動量を考えます．運動量はベクトル量なので少し難しくなりますが，各成分について考えればスカラーの場合と同じです．微小な表面を通して流れ出る運動量（運動量の流量）は

$$
\newcommand{\x}{\bm{x}}
\newcommand{\vvv}{\bm{v}}
v(\x,t)\ \rho(\x,t) \vvv(\x,t) \cdot d\bm{S}
$$

です（これもベクトル量）．これを$${\bm{v}}$$の転置ベクトル$${\bm{v}^{\mathrm{T}}}$$を導入して次のように変形しておくのも便利です．

$$
\newcommand{\x}{\bm{x}}
\newcommand{\n}{\bm{n}}
\newcommand{\vvv}{\bm{v}}
dS\ \rho(\x,t)\ \vvv(\x,t) \vvv^{\mathrm{T}}(\x,t) \n(\x)
$$

また，ニュートンの第二法則によれば運動量の湧き出しは外力から来るので，運動量の湧き出しの和は，単位質量あたりに加わる外力（体積力）を$${F}$$，応力ベクトルを$${\bm{T}}$$として

$$
\int_V d\bm{x}\ \rho(\bm{x},t) F(\bm{x},t) + \int_S dS\ \bm{T}(\bm{x},\bm{n},t)
$$

と書けます（もちろんこれもベクトル量です）．

ここで，ガウスの法則（のテンソルに拡張したもの）

$$
\newcommand{\Div}{\mathrm{div}\,}
\newcommand{\x}{\bm{x}}
\newcommand{\n}{\bm{n}}
\int_S dS\ \bm{T} (\x,\n,t) = \int_V d\x\ \Div T(\x,t)
$$

を用いて，面積分を体積分に直します．ただし，テンソル場の発散は

$$
\newcommand{\Div}{\mathrm{div}\,}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\Div T = \begin{pmatrix}
\pd{T_{xx}}{x} + \pd{T_{xy}}{y} + \pd{T_{xz}}{z}\\
\pd{T_{yx}}{x} + \pd{T_{yy}}{y} + \pd{T_{yz}}{z}\\
\pd{T_{zx}}{x} + \pd{T_{zy}}{y} + \pd{T_{zz}}{z}
\end{pmatrix}
$$

で定義しました．

以上から運動量に関してバランス方程式を立てることができて（これは運動方程式にほかならないのですが），

$$
\newcommand{\Div}{\mathrm{div}\,}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\x}{\bm{x}}
\newcommand{\n}{\bm{n}}
\newcommand{\vvv}{\bm{v}}
\pd{\rho(\x,t)\vvv(\x,t)}{t} = -\Div(\rho(\x,t) \vvv(\x,t) \vvv^{\mathrm{T}}(\x,t)) + \rho(\x,t) F(\x,t) + \Div T(\x,t)
$$

と書けます．

流体がニュートン流体であることと，非圧縮性を仮定して，式を整理すると

$$
\newcommand{\grad}{\mathrm{grad}\,}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\x}{\bm{x}}
\newcommand{\n}{\bm{n}}
\newcommand{\vvv}{\bm{v}}
\pd{\vvv}{t} + (\vvv\cdot \grad) \vvv(\x,t) = F(\x,t) - \frac{1}{\rho}\grad p + \nu \nabla^2 \vvv(\x,t)
$$

が得られます．これはナビエ・ストークス（Navier--Stokes）方程式と呼ばれます．方程式には

$$
\nu = \frac{\mu}{\rho}
$$

の形で粘性が入ってきています．これを動粘性係数といいます．

外力が重力のような保存力だけのとき，

$$
\newcommand{\grad}{\mathrm{grad}\,}
F(\bm{x}) = -\grad \phi(\bm{x})
$$

の形に書くことができるので，外力の項は圧力の項とまとめて扱うことができます．つまり，保存力の場もとでの流体の運動は，外力がないときの運動と本質的にかわりません．そこで，外力がない場合を以下で考えます．

レイノルズ数

流れを特徴づける代表的な長さ$${L}$$，代表的な速度$${U}$$を単位としてナビエ・ストークス方程式を無次元化すると，

$$
\newcommand{\grad}{\mathrm{grad}\,}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\x}{\bm{x}}
\newcommand{\n}{\bm{n}}
\newcommand{\vvv}{\bm{v}}
\pd{\vvv '}{t'} + (\vvv ' \cdot \grad{'}) \vvv '(\x ',t') = - \grad{'} p' + \frac{\mu}{\rho U L} \nabla'^2 \vvv'(\x',t)
$$

と書けます（ここでプライム記号を付けた量はすべて無次元化した量です）．

二つの別の流体の流れが相似になるには，流れの境界の形が幾何学的に相似であることはもちろん必要ですが，それだけでなく，無次元化した運動方程式も同じ形になっていなくてはなりません．したがって，

$$
Re = \frac{\rho U L}{\mu} = \frac{UL}{\nu}
$$

で定義される無次元量が二つの流れについて同じでなければなりません．この数をレイノルズ（Reynolds）数といいます．

流れには層流と乱流があります．レイノルズ数が小さい領域では，ナビエ・ストークス方程式の定常解とよく一致するのに，レイノルズ数がある値（臨界レイノルズ数）よりも大きくなると，極めて複雑な流れとなることがわかりました．前者を層流といい，後者を乱流といいます．理論的には，層流はいかなるレイノルズ数に対しても可能なのにもかかわらず，です．これはカオスや散逸構造という分野につながる奥深い問題です．そしてまだ真に解決したとはいえない問題だと思います．

クエット流れ

ナビエ・ストークス方程式に従う，定常で，一次元の流れを考えてみましょう．非圧縮性の条件から，

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\pd{v_x}{x} = 0
$$

となるので，速度は

$$
v_x = v_x(y,z,t)
$$

という形の流れの方向の座標を含まない関数になることがわかります．それゆえ，ナビエ・ストークス方程式は

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\ppd}[2]{\frac{\partial^2 #1}{\partial #2^2}}
\newcommand{\lr}[1]{\left(#1\right)}
0 = -\frac{1}{\rho} \pd{p}{x} + \nu \lr{\ppd{v_x}{y} + \ppd{v_x}{z}}\\
0 = - \frac{1}{\rho} \pd{p}{y}\\
0 = - \frac{1}{\rho} \pd{p}{z}\\
$$

と簡単になります．下の二式は，圧力が

$$
p = p(x,t)
$$

という形の関数であることを示しています．すると一つ目の式について，

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\ppd}[2]{\frac{\partial^2 #1}{\partial #2^2}}
\newcommand{\lr}[1]{\left(#1\right)}
\underbrace{\nu \lr{\ppd{v_x}{y} + \ppd{v_x}{z}}}_{x\text{を含まない}} = \underbrace{\frac{1}{\rho}\pd{p}{x}}_{y,z\text{を含まない}}
$$

なので，これは時間のみの関数でなければなりません．これを$${\alpha(t)}$$とおきます．

無限に広い二枚の平行な板の間を流体が流れるときは，方程式は

$$
\newcommand{\ppd}[2]{\frac{\partial^2 #1}{\partial #2^2}}
\ppd{v_x}{y} = \frac{\alpha}{\nu}
$$

と簡単になり，その解は

$$
v_x = \frac{\alpha}{2\nu} y^2 + Ay + B
$$

と書けます．圧力勾配がない，つまり$${\alpha = 0}$$のときは，速度分布は線形になります．このような流れをクエット（Couette）流れといいます．

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

以上で流体力学のミニマルの紹介を終わります．数式が多くて少々うんざりされたかもしれません．確かに，物理的な実体を持ったものなのに，数式にしてしまうとなんだか味気なさを感じる部分はあります．このノートではナビエ・ストークス方程式を導くところまでを一番の目標にしていたので，今回のお話としては，数学的なお膳立てを経て，ようやくスタート地点に立ったにすぎない感じもします．さまざまな楽しい現象については扱えていないのは残念なところですが，まだ私には流体力学の面白さを生き生きと語れるほどの力もありません．もう少し私が流体力学の魅力を理解できたら，そのときはまた記事を書くことにします．□