
【物理数学】フォッカー・プランク方程式【確率論③】
前回,マスター方程式を導きましたが,マスター方程式は時間微分と状態の積分からなる方程式なので大きな自由度の系を扱うにはなかなか複雑なものでした.今回は,状態の間の「近さ」に着目することで,マスター方程式を形式的に微分方程式の形にすることを目標にします.ただし,状態間の距離を考えることに意味がないような状況もあるので,位置や密度など,定量的に状態間の「距離」を測れるようなものに限定して考えることになります.
クラマース・モヤル方程式
前回導いたマスター方程式とは,過程がマルコフ過程であるときに,ある時刻においてある状態を取るような確率密度の時間発展を記述する方程式のことで
$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\pd{}{t} f(x,t) = \int dx' \Bigl[
-W(x' \mid x,t) f(x,t) + W(x \mid x', t) f(x', t)
\Bigr]
$$
と表されていました.状態間の飛躍(jump)を$${r = x' - x}$$と置いて,遷移速度を$${W(x'\mid x,t) = w(r,x,t)}$$という表記に改めれば,マスター方程式は
$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\pd{}{t}f(x,t) = \int dr \Bigl[ -w(r,x,t) f(x,t) + w(-r, x + r, t) f(x+r,t) \Bigr]
$$
と表されます.ここで,飛躍について右辺第二項をテイラー展開します.つまり,
$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\ppd}[2]{\frac{\partial^2 #1 }{\partial #2 ^2}}
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
&\int dr\ w(-r, x+r, t) f(x+r, t) \\
&= \int dr \lr{w(-r,x,t) f(x,t) + r \pd{}{x}w(-r,x,t) f(x,t) + \frac{r^2}{2} \ppd{}{x} w(-r,x,t) f(x,t) +\cdots}
\end{align*}
$$
のように展開します.ここで右辺はすべての飛躍で積分しているので,飛躍の符号を$${r \to -r}$$に置き換えても問題ありません.このように置き換えたものをもとのマスター方程式に代入すれば,マスター方程式の右辺第一項と打ち消し合う部分ができて,残るのは
$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\ppd}[2]{\frac{\partial^2 #1 }{\partial #2 ^2}}
\newcommand{\lr}[1]{\left(#1\right)}
\pd{}{t} f(x,t) = \int dr \lr{-r \pd{}{x} w(r,x,t) f(x,t) + \frac{r^2}{2} \ppd{}{x} w(r,x,t) f(x,t) + \cdots}
$$
となります.ここで,飛躍についての積分を先に実行しておいて,
$$
\begin{align*}
A(x,t) &= \int dr \ r w(r,x,t)\\
B(x,t) &= \int dr \ r^2 w(r,x,t)
\end{align*}
$$
と置きます.これらは統計学でモーメントと呼ばれる量(ただし,今は時間あたりの飛躍についてのモーメント)です.特にいま上に書いた一次のモーメント,2次のモーメントは統計学ではそれぞれ平均,分散といいますが,物理的に意味がある文脈ではそれぞれドリフト係数,拡散係数とも呼びます.こうして
$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\ppd}[2]{\frac{\partial^2 #1 }{\partial #2 ^2}}
\newcommand{\lr}[1]{\left(#1\right)}
\pd{}{t} f(x,t) = - \pd{}{x} A(x,t) f(x,t) + \frac{1}{2}\ppd{}{x} B(x,t) f(x,t) + \cdots
$$
が得られました.これをクラマース・モヤル(Kramers-Moyal)方程式といいます.ポイントは,マスター方程式を「飛躍」についての式に形式的に書き換えることで,状態間の相対的な差で展開したことにあります.
フォッカー・プランク方程式
状態間の差が大きく離れているようなところが効いてこないようなとき,とくにクラマース・モヤル方程式の右辺の三階微分以上の展開係数が0に等しいとき,クラマース・モヤル方程式はもちろん
$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\ppd}[2]{\frac{\partial^2 #1 }{\partial #2 ^2}}
\newcommand{\lr}[1]{\left(#1\right)}
\pd{}{t} f(x,t) = - \pd{}{x} A(x,t) f(x,t) + \frac{1}{2}\ppd{}{x} B(x,t) f(x,t)
$$
と書くことができます.これがフォッカー・プランク方程式です.(数学の分野ではコルモゴロフの前進方程式と呼ばれます.)
フォッカー・プランク方程式は,マスター方程式の特別な場合ですが,物理的な過程を問題にするときにはよく顔を出してきます.例えば,拡散方程式はフォッカー・プランク方程式の特別な場合です.広くフォッカー・プランク方程式が現れる背後には何があるのでしょうか.これは今回は詳しく扱いませんが,中心極限定理というものが働いていることの現れということができます.
今回は遷移確率を用いた方程式からからフォッカー・プランク方程式を導いたわけですが,むしろ遷移確率は求めるべきものであることに注意しましょう.物理では観測できるのはドリフト係数や拡散係数といった量なので,直接フォッカー・プランク方程式を書き下すことが多いのです.または,先に物理的なモデルに基づいて運動方程式を立てると,そこからドリフト係数や拡散係数を計算することができるので,やはり直接フォッカー・プランク方程式を書き下すことができます.
補足:パヴーラ(Pawula)の定理
クラマース・モヤル方程式の展開係数は,実はパヴーラの定理というものによって制限がつきます.パヴーラの定理の主張は,「もし偶数階微分の展開係数が0であるものが存在したら,三階微分以上の展開係数はすべて0になる」というものです.これはシュワルツの不等式
$$
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
&\lr{\int f(x) g(x) h(x) dx }^2 \leq \int f(x) g(x)^2 dx \int f(x) h(x)^2 dx\\
& f(x): \text{ 負でない関数}, g(x),h(x): \text{ 任意の関数}
\end{align*}
$$
を用いて証明することができます.ポイントは,確率密度が負でないことからパヴーラの定理の主張が成り立つということです.したがって,摂動展開だと思って三階以上の展開係数まででクラマース・モヤル方程式を打ち切ると,確率密度が負になる状態で展開していることになるのです.しかし,これが悪いということを必ずしも意味しません.確率密度の負の値は非常に小さいので,よく起こるイベントを記述するような場合には,正確な確率分布で計算した場合とよく一致します.フォッカー・プランク方程式でよく記述できる場合はこのようなことは問題にならないので安心です.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
では,前回のカエルの問題の続きを考えましょう.問題を再掲します.
例題
カエルたちが石1,石2の上を飛び移っています.カエルは今いる石だけから判断して,飛び移るかどうかを確率的に決めるとします.時間が 1 経ったのちに石1から石2に飛び移る確率を0.6,とどまる確率を0.4とし,石2から石1に飛び移る確率を0.2,とどまる確率を0.8とします.このカエルたちはこの2つの石の上以外にはどこへも行かないし,カエルどうしで話し合ったりなどはしないとします(つまり孤立系を考え,カエルどうしは独立ということ.なんだか哀れですが......).カエルの分布の時間変化を考えよう.
これは次のようなグラフで表されます.

前回の最後に言ったように,ある瞬間に石1にいるカエルの数が$${x(t)}$$となる確率を考え,この確率密度を$${f(x,t)}$$と置きます.ただし,カエルの数は本来離散的な値を取るので確率密度というのは変です.しかし,ここではカエルがたくさんいるとして,実現値は滑らかな値を取ると近似しても十分良いということにします.そうすれば,カエルの数で微分するということもそんなに変ではなくなります.
まずは,フォッカー・プランク方程式のドリフト係数を求めます.石1にいるカエルの数の変化が状態の「飛躍」なので,飛躍速度は,石1から石2への飛び移りの数をダミー変数とした組み合わせを用いて計算できて,
$$
\begin{align*}
&w(r,x,t) \\
&= \sum_{a=0}^x \frac{x!}{a! (x-a)!} 0.6^a 0.4^{x-a} \frac{(N-x)!}{(a+r)!(N-x-a-r)!} 0.2^{a+r} 0.8^{N-x-a-r}
\end{align*}
$$
により計算されます(図参照).
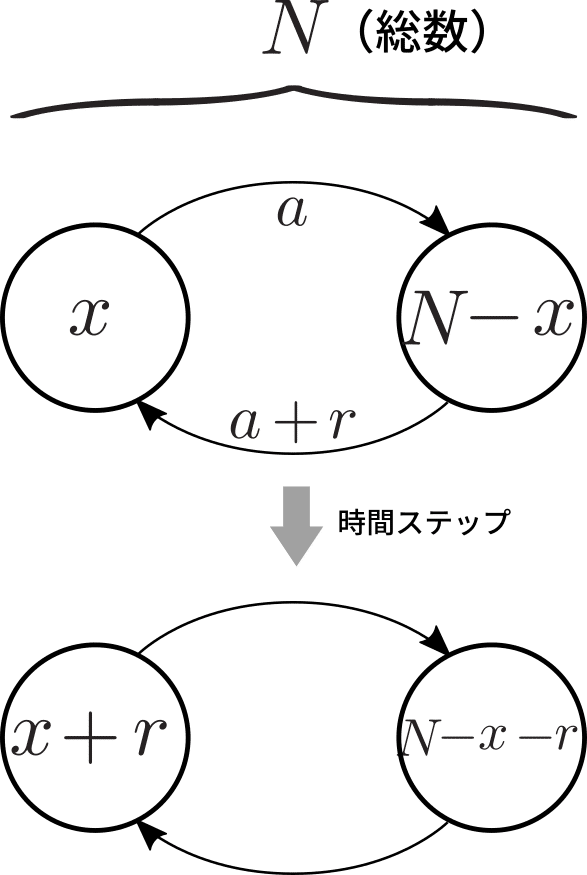
飛躍の速度の1次モーメントがドリフト係数なので,
$$
\begin{align*}
A &= \sum_{r} r \sum_{a=0}^x \frac{x!}{a! (x-a)!} 0.6^a 0.4^{x-a} \frac{(N-x)!}{(a+r)!(N-x-a-r)!} 0.2^{a+r} 0.8^{N-x-a-r}
\end{align*}
$$
を計算すれば良いことになります.(細かく見ると飛躍のとりうる値はダミー変数の取り方に依存して制限を受けているので微妙にこの式はおかしいのですが,境界が問題にならないような設定では概ねこれで計算して良いと思われます.)和を取る順番を入れ替えて先に飛躍について和を計算しますと
$$
\begin{align*}
&\sum_r r \frac{(N-x)!}{(a+r)!(N-x-a-r)!}0.2^{a+r} 0.8^{N-x-a-r}\\
&= \sum_r (a+r-a) \frac{(N-x)!}{(a+r)!(N-x-a-r)!}0.2^{a+r} 0.8^{N-x-a-r}\\
&= 0.2(N-x) \sum_r \frac{(N-x-1)!}{(a+r-1)!(N-x-a-r)!} 0.2^{a+r-1} 0.8^{N-x-a-r} \\
&\quad -a \sum_r \frac{(N-x)!}{(a+r)!(N-x-a-r)!}0.2^{a+r} 0.8^{N-x-a-r} \\
&= 0.2(N-x) - a
\end{align*}
$$
となります.二項展開の公式
$$
\sum_k \binom{n}{k} a^k\ b^{n-k} = (a+b)^n
$$
を用いると和がうまく$${1}$$になるように式変形しています.よって,(再び二項展開の公式を駆使して)
$$
\begin{align*}
A &= \sum_a^x \bigl( 0.2(N-x) -a \bigr)\frac{x!}{a! (x-a)!} 0.6^a 0.4^{x-a}\\
&= 0.2(N-x) - 0.6 x = 0.2N - 0.8 x
\end{align*}
$$
となります.
次に,拡散係数は
$$
\begin{align*}
B = \sum_{r=0}^{N-x-a} r^2 \sum_{a=0}^x \frac{x!}{a! (x-a)!} 0.6^a 0.4^{x-a} \frac{(N-x)!}{(a+r)!(N-x-a-r)!} 0.2^{a+r} 0.8^{N-x-a-r}
\end{align*}
$$
により計算されます.
$$
r^2 = (a+r)(a+r-1) + (1-2a) (a+r) + a^2
$$
と変形できることに注意して,ドリフト係数のときと同様のテクニックで計算します.結果は,
$$
\begin{align*}
B &= 0.04 (N-x)(N-x-1) + 0.2(N-x) - 0.24(N-x)x + 0.36 x(x-1) + 0.6 x\\
&= 0.04 N^2 + 0.16N - 0.32Nx + 0.64x^2 + 0.08x
\end{align*}
$$
となります.
以上から,フォッカー・プランク方程式として,
$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\ppd}[2]{\frac{\partial^2 #1 }{\partial #2 ^2}}
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
\pd{f(x,t)}{t} = &-\pd{}{x} (0.2N - 0.8 x) f(x,t) \\
&+ \frac{1}{2}\ppd{}{x} ( 0.04 N^2 + 0.16N - 0.32Nx + 0.64x^2 + 0.08x)f(x,t)
\end{align*}
$$
が得られました.
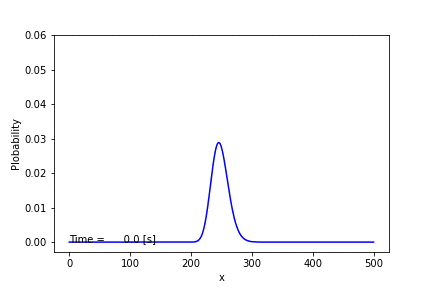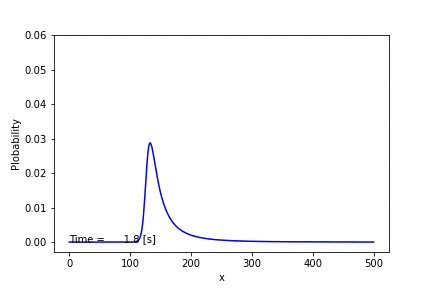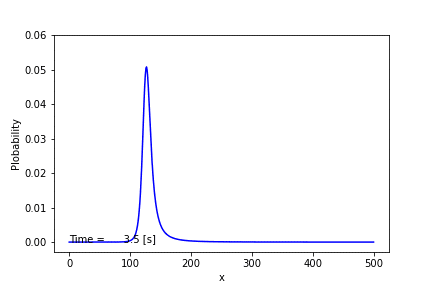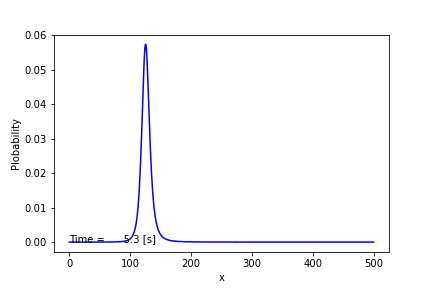
このダイナミクスを紙と鉛筆を使って解くことはできないので,数値計算に頼ることにします.(フォッカー・プランク方程式が解析的に解けるものはごく限られています.)全部で500匹のカエルがいて,初期条件は250匹のカエルが石1にいるとしたときに,数値的に解いてみました.その結果,次のアニメーションように石1にいるカエルの数の確率は時間発展することがわかりました.時間が十分経てば125匹にピークを持つ定常分布に落ち着いています.この結果は前回の結果からも支持されますが,今回は確率分布の時間変化まで追うことができました.(微分方程式を解くには,クランク・ニコルソン法という手法を用いました.また,方程式を解くためのアルゴリズムとしてはガウス・ザイデル法を用いました.)
まとめ
マスター方程式を状態間の飛躍に着目して微分方程式の形にし,二階までの微分方程式の形にしたもの,すなわちドリフト係数と拡散係数を用いて記述したものをフォッカー・プランク方程式といい,物理的な確率過程の多くを記述する.
おまけ:上記アニメーションのPythonのソースコード
(改良の余地はあると思います.お気づきの点があればぜひ教えてください.このプラグラムを書くのに思ったよりも苦戦して記事の更新にすごく時間がかかりました.このコードの解説はこちらの記事でしています.)
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# input parameter
dx = 1.0
xtot = 500 # カエル総数
dt = 0.0004
dur = 5.3 # 計算期間
tout = 0.02 # 間引き時間間隔
# calclated parameter
nx = int(xtot+1 / dx) # 空間的分割数
nt = int(dur / dt) # 時間ステップ数
nout = int(tout / dt) # 間引き
c1 = dt/dx/2
c2 = c1/dx
A = lambda x : 0.2 * xtot - 0.8 * x
B = lambda x : 0.04 * xtot**2 + 0.16 * xtot - 0.32 * xtot * x + 0.64 * x**2 + 0.08 * x
# initial condition
f_init = 0.0
f = np.full(nx, f_init) # fは f[0] から f[nx-1] まで
f[250] = 1.0
time = 0.0
f_old = np.zeros(nx)
# graph data array
ims = []
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
gx = np.zeros(nx)
for i in range (nx):
gx[i] = i * dx
# loop calculation
itr_max = 10000
for n in range(1, nt + 1): # nt まで時間発展
f_sum = sum(f)
for i in range(nx):
f_old[i] = f[i]
for itr in range(itr_max): # 繰り返し計算
resd = 0.0
eps = 1.0e-8
for i in range(1, nx-1): # 境界は除外
fx = f[i]
f[i] = ( (1 -c2 * B(i)) * f_old[i] \
+ 1/2 * ( (-c1 * A(i+1) + c2 * B(i+1)) * f_old[i+1] + (c1 * A(i-1) + c2 * B(i-1) ) * f_old[i-1] )\
+ 1/2 * ( (-c1 * A(i+1) + c2 * B(i+1)) * f[i+1] + (c1 * A(i-1) + c2 * B(i-1) ) * f[i-1] ) )\
/ (1 + B(i) * c2)
resd += abs(f[i] - fx)
if resd <= eps:
break
# apply boundary condition
f[0] = B(1) * f[1]/(dx * A(0) + B(0))
f[nx-1] = (dx * A(nx-2) + B(nx-2)) * f[nx - 2] / B(nx-1)
time += dt
# data thining out
if n % nout == 0:
print('n: {0: 7d}, time: {1: 8.1f}, sum: {2: 5.3f}, itr:{3:4d}'.format(n, time, f_sum, itr))
im_line = ax.plot(gx, f, 'b')
im_time = ax.text(0, 0, 'Time = {0: 8.1f} [s]'.format(time))
ims.append(im_line + [im_time])
# plot
ax.set_xlabel('x')
ax.set_ylabel('Plobability')
anm = animation.ArtistAnimation(fig, ims, interval = 50)
anm.save('animation_kaeru.gif', writer = 'pillow')
plt.show()更新履歴
20211021 執筆
20211022 図の追加
クオリティの高いノートをたくさん書けるように頑張ります!
