
簡易版コラッツ予想で遊ぼう
「コラッツ予想」という数学の問題があります。
コラッツ予想
以下のような数列を考える。
・$${C_0(c)=c}$$
・$${C_{n+1}(c)=\begin{cases}\frac{1}{2}C_n(c)&\text{if}&C_n(c)\equiv0\pmod2\\3C_n(c)+1&\text{if}&C_n(c)\equiv1\pmod2\end{cases}}$$
このとき、いかなる自然数$${c}$$についても$${C_m(c)=1}$$を満たす自然数$${m}$$が存在するだろう。
この問題自体が未解決の超難問として有名(多分)なのですが、この問題と似たような形式の派生問題を無数に考えることができ、その中には本来のコラッツ予想とは全く違った性質を持つものも存在します。
この記事では、コラッツ予想派生問題の中でも比較的簡単そうに見える問題と、その関連問題について紹介します。
※先行研究例等はほとんど調べていません。
簡易版コラッツ予想
まず、簡易版コラッツ予想を以下の通り定義します。
簡易版コラッツ予想
以下のような数列を考える。
・$${A_0(c)=c}$$
・$${A_{n+1}(a)=\begin{cases}\frac{1}{2}A_n(a)&\text{if}&A_n(a)\equiv0\pmod2\\A_n(a)+1&\text{if}&A_n(a)\equiv1\pmod2\end{cases}}$$
このとき、いかなる自然数$${a}$$についても$${A_m(a)=1}$$を満たす自然数$${m}$$が存在するだろう。
コラッツ予想と違うのは第$${n}$$項が奇数のときの処理で、3倍して1を足していたのが3を掛けなくなっています。
数値の増減の不規則性というのはコラッツ予想を難しくしている要素の一つですが、簡易版では数値の増加が弱められているので元の問題よりは簡単になっていることが予想できます。
解決
簡易版コラッツ予想は、実は高校レベルの知識で解決可能です。
考え方としては「$${A_n(a)}$$はいつか必ず初期値より小さくなるので、1~Nまでの全ての自然数で成り立てば数学的帰納法によりN+1でも成り立つ」という感じで、$${A_n(a)}$$が初期値より小さくなることは場合分けをして以下のように示せます。
$${a}$$が偶数のとき
$${A_0(a)=a=2k}$$
$${A_1(a)=k< a}$$
$${a}$$が奇数のとき
$${A_0=a=2k+1}$$
$${A_1(a)=2k+2}$$
$${A_2(a)=k+1< a}$$
これに気付くことができれば、あとは$${a=1}$$のときを確認すればOKです。
ちなみにこの「$${A_n(a)}$$は初期値より小さくなる」という論法は、本来のコラッツ予想で使おうとするとこうなります。
$${C_0(c)}$$が偶数のとき
$${C_0(c)=c=2k}$$
$${C_1(c)=k< c}$$
$${c}$$が奇数のとき
$${C_0(c)=c=2k+1}$$
$${C_1(c)=6k+4}$$
$${C_2(c)=3k+2}$$
$${c}$$が奇数という条件だけだとこれ以上計算できないので、奇数のケースを更に場合分けします。
$${c}$$を4で割った余りが1のとき
$${C_0(c)=c=4k+1}$$
$${C_1(c)=12k+4}$$
$${C_2(c)=6k+2}$$
$${C_3(c)=3k+1< c}$$
$${c}$$を4で割った余りが3のとき
$${C_0(c)=4k+3}$$
$${C_1(c)=12k+10}$$
$${C_2(c)=6k+5}$$
$${C_3(c)=18k+16}$$
$${C_4(c)=9k+8}$$
4で割って3余るケースが判定できなかったので、更に場合分けしてみます。
$${c}$$を8で割った余りが3のとき
$${C_0(c)=c=8k+3}$$
$${C_1(c)=24k+10}$$
$${C_2(c)=12k+5}$$
$${C_3(c)=36k+16}$$
$${C_4(c)=18k+8}$$
$${C_5(c)=9k+4}$$
$${c}$$を8で割った余りが7のとき
$${C_0(c)=c=8k+7}$$
$${C_1(c)=24k+22}$$
$${C_2(c)=12k+11}$$
$${C_3(c)=36k+34}$$
$${C_4(c)=18k+17}$$
$${C_5(c)=54k+52}$$
$${C_6(c)=27k+26}$$
今度はどちらも小さくなりませんでした。
この後も16で割った余り、32で割った余り、64で割った余り、・・・と場合分けを細かくしていくと、以下の図のように判定できないケースがどんどん増えていくようです。

樹形図
先程樹形図が出てきましたが、コラッツ予想に関する樹形図と言えばこちらの方の図を思い浮かべる人が多いと思います。

この図は$${C_n(c)}$$の計算を逆向きに辿った図で、20回以内の計算で1に辿り着く初期値とその過程を表しています。
$${A_n(a)}$$の方で同じようなことをしてみると、こんな図ができました。

※計算回数の上限は20回ではなく10回になっています。
この図をよく観察してみると、連続する自然数が縦に並んでいる箇所がたくさん見つかります。
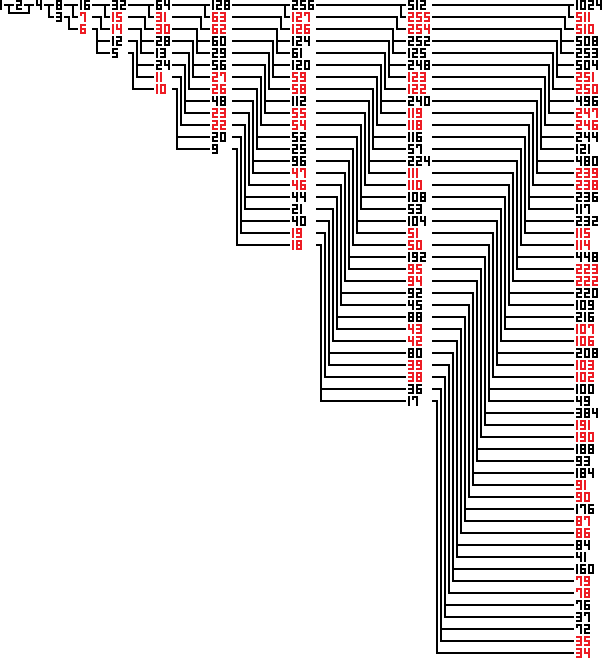
図中の数の並びは「Nの右に2Nを置き、Nが偶数なら2Nの下にN-1を置く」という規則で決まっており、この規則に従うと以下のように4以上の偶数から必ず連続する自然数の並びが発生するようです。

また、各列にある数の個数を数えてみると、以下のようになっていました。
1,1,1,2,3,5,8,13,21,34,55
初項を無視すると、この数列はフィボナッチ数列と一致します。
この性質は、次のように説明できます。
まず、左から$${n}$$番目(左端は$${n=0}$$)の列にある数の個数を$${s_n}$$とし、偶数の個数を$${e_n}$$、奇数の個数を$${o_n}$$とします。
$${2\leq n}$$のとき、$${e_{n+1}}$$と$${o_{n+1}}$$は以下のような漸化式で求めることができます。
$${\begin{cases}e_{n+1}=e_n+o_n\\o_{n+1}=e_n\end{cases}}$$
この式を使うと、$${s_{n+2}}$$は以下のように表せます。
$${s_{n+2}\\=e_{n+2}+o_{n+2}\\=e_{n+1}+o_{n+1}+e_{n+1}\\=e_{n+1}+o_{n+1}+e_n+o_n\\=s_{n+1}+s_n}$$
この式はフィボナッチ数列の漸化式と同じで、$${s_2=F_3}$$、$${s_3=F_4}$$であることから$${s_n}$$が途中からフィボナッチ数列と一致することがわかります。
ちなみに最初の方の項が例外になるのはループを考慮して2←1という遷移を省略しているためで、4の下に1を置いてその続きも全部書いていった場合は$${s_0}$$からフィボナッチ数列と一致するようになります。(項番号は1つズレたままです)
通常のコラッツ予想で似たようなこと(個数の計算)をする場合、漸化式を導出できなくて失敗します。
簡易版では分岐が発生する条件が2で割った余りに依存し、分岐した後の項も奇数か偶数かがはっきりしていました。
通常のコラッツ予想の場合は6で割った余りによって分岐するかどうかが決まるのですが、分岐後は6で割った余りの情報が消失するため、どの余りの数が何個あるのかわからなくなります。

(6で割って4余る数は分岐するが、分岐後は6で割った余りがわからない)
このほかにも簡易版コラッツ予想の樹形図には通常よりも便利な性質がいくつかあるため、通常のコラッツ予想では上手くいかない「1から始まる樹形図にすべての自然数が出現することを示す」という方針の証明もできる気がします。
派生問題
こんな数列を考えます。
$${A_0(a,k)=a}$$
$${A_{n+1}(a,k)=\begin{cases}\frac{1}{2}A_n(a,k)&\text{if}&A_n(a,k)\equiv0\pmod2\\A_n(a,k)+k&\text{if}&A_n(a,k)\equiv1\pmod2\end{cases}}$$
ただし、$${a}$$は自然数で$${k}$$は1以上の奇数とします。
$${k=1}$$のときが簡易版コラッツ予想に出てくる数列で、それ以外のときは違う数列になります。
まず、$${A_n(1,k)}$$を計算して1に戻ってくるかどうかを確かめてみます。
k=3 : 1,4,2,1
k=5 : 1,6,3,8,4,2,1
k=7 : 1,8,4,2,1
k=9 : 1,10,5,14,7,16,8,4,2,1
k=11 : 1,12,6,3,14,7,18,9,20,10,5,16,8,4,2,1
k=13 : 1,14,7,20,10,5,18,9,22,11,24,12,6,3,16,8,4,2,1
どうやら必ず1に戻ってくるっぽいですが、サイクルの周期の長さは不規則です。
$${k=1}$$のときの性質は先述の通り単純でしたが、それ以外のケースの性質は私にはまだ把握し切れていません。
というわけで、$${A_n(a,k)}$$に関しては(私の中では)未解決の疑問が多く残されています。
疑問1:いかなるの3以上の奇数$${k}$$に対しても、$${A_m(1,k)=1}$$を満たす自然数$${m}$$は存在するの?
疑問2:$${k}$$を動かしたときの、$${A_n(1,k)}$$の周期の変化の規則性は?
$${A_n(a,1)}$$では数列の収束先は1を含む2周期サイクルのみでしたが、$${1< k}$$では以下のように1を含まないサイクルが存在するようになります。
k=3 : 3,6,3
k=5 : 5,10,5
k=7 : 7,14,7
k=7 : 3,10,5,12,6,3
$${k=1~35}$$までで存在するサイクルを調べてみたところ、以下のようになりました。

どうやら$${1< k}$$では1を含むサイクルのほかに$${k}$$を含む2周期のサイクルが存在し、$${k}$$の値次第ではその他のサイクルが存在したりしなかったりするようです。
なお、$${A_n(a,1)}$$が1に収束することの証明で行った計算を$${1< k}$$でやると、「$${k< a}$$の場合、$${A_n(a,k)}$$は初期値より小さい値をとる」という事がわかります。
このことを使うと、「$${A_n(a,k)}$$が無限大に発散することはない」という事が証明でき、さらにサイクルの個数は有限個で、$${a=1~k}$$の数列を総当たりすれば全てのサイクルを発見できることも分かります。
また、これ以外に有用な性質として以下のようなものがあります。
$${A_n(a,rk)=rA_m(b,k)}$$が成り立つならば$${A_{n+1}(a,rk)=A_{m+1}(b,rk)}$$も成り立つ。
例えば$${A_1(2,3)=1}$$と$${A_0(5,15)=5}$$の間には$${5×A_1(2,3)=A_0(5,5×3)}$$という関係がありますが、この後の項にも
$${5×A_2(2,3)=A_1(5,5×3)}$$
$${5×A_3(2,3)=A_2(5,5×3)}$$
$${5×A_4(2,3)=A_3(5,5×3)}$$
・・・という関係が成立し続けます。
この性質により、$${A_n(a,15)}$$には「$${A_n(a,3)}$$のサイクルの要素を全て5倍した値からなるサイクル」が存在します。
実際、$${A_n(a,3)}$$のサイクルは以下の2種類で、
1,4,2,1
3,6,3
一方で$${A_n(a,15)}$$には以下のようなサイクルがあります。
5,20,10,5
15,30,15
なお、同じ原理により$${A_n(a,15)}$$には「$${A_n(a,5)}$$のサイクルの要素を全て3倍した値からなるサイクル」が存在します。
$${A_n(a,5)}$$が持つ2つのサイクルの内の1つは、3倍すると「$${A_n(a,3)}$$のサイクルを5倍したサイクル」の片方と同じサイクルになってしまいますが、$${A_n(1,3)}$$と$${A_n(1,5)}$$に対応するサイクルは$${A_n(a,15)}$$の中ではそれぞれ別のサイクルとして存在します。
一般に、$${r\neq k}$$であれば$${A_n(a,rk)}$$のサイクルの中には$${A_n(1,k)}$$と$${A_n(1,r)}$$に対応するサイクルがそれぞれ別のサイクルとして存在するようです。
このことから、$${A_n(a,k)}$$が持つサイクルの個数は$${k}$$の約数の個数以上であると予想できます。
疑問3:$${3< k}$$なら$${A_n(a,k)}$$のサイクルの個数$${l_k}$$について$${d(k)\leq l_k<\frac{k}{2}}$$が成り立つの?
※$${d(k)}$$は$${k}$$の約数の個数
下からの評価は先述の通りで、上からの評価に関してはこれまでの説明から$${l_k\leq k}$$であることはわかるものの、実際の計算結果では半分以下に収まるように見えます。
疑問4:$${A_n(a,3^m)}$$の1を含むサイクルの周期って$${3^m}$$なの?
これに関しては背景となりそうな性質が一切見えていないのですが、実際に検証してみると成り立っていそうです。

また、$${A_n(1,5^m)}$$の場合は周期が$${6×5^{m-1}}$$になるっぽいので何かしらの法則性がありそうだと思いきや、$${A_n(1,5×3^m)}$$や$${A_n(1,7^m)}$$だと規則性が見られず、本当に謎です。
