
第3回高周期ジュリア集合選手権
この記事は日曜数学 Advent Calendar 2022 - Adventarの18日目の記事です。
どうも、108Hassiumです。
複素数たちがさまざまな関数のジュリア集合における周期を競い合う高周期ジュリア集合選手権の第3回大会を開催します。
私が書いた第2回以前の記事を読んでいない方は「お前はいきなり何を言っているんだ」と思ったでしょうから、本題に入る前にまず必要な知識および企画趣旨の説明をします。
記事内に文章を理解したい人は目を通していただいた方がいいと思いますが、文章をガン無視して画像だけを流し見していってもそこそこ楽しめると思います。
あとついでに前回までの記事も置いておくので興味のある方は読んでみてください。
☟第2回
☟第1回
☟第0回
前提知識
ジュリア集合
$${z_{n+1}=f(z_n)}$$が無限大に発散しないような初期値$${z_0}$$全体の集合を、「$${f(z)}$$のジュリア集合」とする。
wikipedia等に載っている(おそらく正式であろう)定義とは異なりますが、利便性等の都合によりこちらの定義を使用します。
同値な言いかえですらない完全な別物ですが、この記事では厳密な数学数学した議論をするわけではないので特に問題はないでしょう。
以下の画像は、$${f(z)=z^2-0.2+0.7i}$$としたときのジュリア集合の画像です。

図中の黒い領域がジュリア集合で、外側のカラフルな領域がジュリア集合に含まれない点を表しています。
$${z_0}$$が黒い領域の中にあるとき、$${z_n}$$の値は0.121+0.141i→-0.203+0.732i→-0.695+0.402i→0.121+0.141i…(各値は近似値)という3周期のループに近づいていきます。

このように近くにある値を引き寄せるサイクルを「吸引的サイクル」と呼び、$${z_n}$$が到達し得る吸引的サイクルの周期を「$${f(z)}$$のジュリア集合の周期」と呼ぶことにします。
また、吸引的サイクルに到達する初期値が密集している領域を「収束領域」と呼ぶことにします。
先程の図だと、黒い領域(外周を除く)全体が収束領域です。

マンデルブロ集合
$${z_0=\alpha}$$、$${z_{n+1}=f(z_n,c)}$$が無限大に発散しないような$${c}$$全体の集合を、「$${\alpha}$$を初期値とする$${f(z,c)}$$のマンデルブロ集合」とする。
普通はマンデルブロ集合といえば$${\alpha=0}$$、$${f(z,c)=z^2+c}$$に限定したものを指すようですが、それだと不便なのでこの記事ではこの定義を使います。
初期値を指定しない場合は、$${f(z,c)}$$の$${z}$$についての臨界点($${f(z,c)}$$の導関数の零点)を初期値にしたものを表すとします。
なんで急に臨界点が出てくるのかというと、臨界点を初期値にするとジュリア集合の性質を調べるのに使えるからです。
仕組みはわかりませんが、$${f(z,\alpha)}$$($${\alpha}$$は定数)のジュリア集合が収束領域を持つかどうかは、$${\alpha}$$が$${f(z,c)}$$のマンデルブロ集合に含まれるかどうかで判別できるようです。
例えば、$${z^2+\alpha}$$という形の関数のジュリア集合の$${\alpha}$$の位置を$${z^2+c}$$のマンデルブロ集合と重ねると以下のようになります。

御覧の通り、$${\alpha}$$がマンデルブロ集合の中にあるときは$${f(z,\alpha)}$$のジュリア集合は収束領域を持ち、外側にあるときは収束領域を持ちません。
なお、$${f(z,c)}$$の選び方によっては臨界点が複数存在することがあります。
例えば$${\frac{z^3}{3}-\frac{z^2}{2}+c}$$を$${z}$$で微分すると$${z^2-z}$$になり、$${z^2-z=0}$$の解は$${z=0}$$と$${z=1}$$の2つが存在します。


このようなケースでは、$${z_n}$$は初期値ごとに異なった吸引的サイクルを持つことがあり、ジュリア集合も異なるサイクルに収束する領域が混在することがあります。

(z_0=0と同じサイクルに収束する領域は緑、z_0=1の方は青)
なお、臨界点が複数存在すれば吸引的サイクルが同じ個数だけ存在するというわけではなく、発散してしまうものとそうでないものに分かれたり同じサイクルに合流したりすることもあります。
ただし、サイクルの個数が臨界点の個数を超えたり、臨界点を初期値とする数列から到達できないサイクルが存在するといったことは起きないようなので、全ての臨界点に対して$${z_n}$$を計算することで$${f(z,c)}$$のジュリア集合がどんなサイクルを持つかを判定できるようです。
便利ですね。(仕組みは知りません)
企画概要
高周期ジュリア集合選手権とは、複素関数$${f(z,c)}$$を「競技」とみなし、参加条件(後述)を満たす複素定数$${\alpha}$$を「選手」とし、各選手が$${f(z,\alpha)}$$のジュリア集合の周期の大きさを競い合う仮想的イベントです。
例えば、参加条件を「{-0.2+0.7i,-0.5+0.6i,-1.4}に含まれる」として$${z^2+c}$$という競技を実施した場合、各選手の記録は
-0.2+0.7i:3周期
-0.5+0.6i:5周期
-1.3:4周期
となり、周期が最も大きかった-0.5+0.6iの優勝となります。



※上の3枚の画像では、ジュリア集合の収束領域の内側を周期と収束速度を使って彩色しています。以降、この記事では同じような方法によって彩色した画像を使用します。
この記事では5つの競技を実施し、各競技における1位から5位までの結果をジュリア集合の画像と多少の解説とともに発表します。
よくわからないという人は、「ジュリア集合の記事がたくさん載っている記事」と思って画像だけでも見ていってください。
さて、先程の例では説明のために参加条件を恣意的に決めましたが、実際の大会では異なった形式の参加条件を使用します。
例えば第0回大会では$${z^2+c}$$という競技に対して「実部と虚部の小数点以下は2桁まで、実部は-2から1、虚部は0から2まで」という条件を設定していました。
例えば-1.3や0.24+0.51iは参加条件を満たしていますが、$${-\sqrt{2}}$$は無理数であるため小数点以下が2桁に収まらず、$${0.5-0.6i}$$は虚部の範囲が0~2からはみ出すのでどちらも参加できません。
2つの条件のうち小数点以下の制限は、「キリのいい値で周期の長いジュリア集合を生成できるようなパラメータを知りたい」という企画そのものの根本的な動機を反映したものです。
ではもう一つの条件、実部と虚部の制限は何なのかというと、これは$${z^2+c}$$のマンデルブロ集合が持つ性質によるものです。

この画像では実部も虚部も-2から2までの範囲を描画していますが、これより外側の範囲には黒い領域(=収束領域を持つジュリア集合を生成する点の集まり)は存在しません。
「実部は-2から1まで」という制限はこの性質によるものです。(実部のプラス側はもっと狭くしてもいいのですが、面倒なのでキリのいい値に設定しました)
そして虚部ですが、実は$${z^2+c}$$のジュリア集合には「$${c=x+yi}$$と$${c=x-yi}$$のジュリア集合は形も周期も全く同じ」という性質があります。

なので$${c}$$の虚部が負の場合をわざわざ調べても結果が被って面白くないため、参加条件から虚部が負の値が除外されているのです。
ちなみに、$${z^2+c}$$のマンデルブロ集合が実軸に対して線対称になっているのはこの性質と関係があり、他の関数でもマンデルブロ集合の対称性が周期の被りと関係していることがよくあります。(対称性があるからと言って必ずしも周期被りが生じるわけではなくて、第2回大会の記事でそのことについて少し説明しています)
なお、参加条件を満たしている選手でも、臨界点を初期値とする数列が以下の条件を満たすものはランキング選考からは除外されます。
発散する
周期が$${\infty}$$(非周期的)である
前者に関しては「記録なし」のようなものと考えればランキングに入らないのは当然のことですが、後者の扱いはちょっと厄介です。
$${z^2+c}$$のジュリア集合において、非周期サイクルを持つ$${c}$$の値は2種類あります。
まずは0.37+0.16iのような「マンデルブロ集合の境界線上に位置する値」です。

この場合は、$${z_n}$$は閉曲線上を非周期的に巡回する挙動になります。
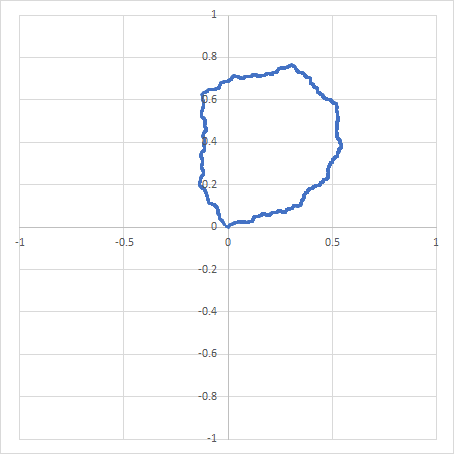
(非周期的なので、曲線全体が点で埋め尽くされている)
もう一つは-1.6のような、マンデルブロ集合の左側にある線の上にある値です。

線の上にはマンデルブロ集合本体とそっくりな形の小さな「飛び地」が散らばっていますが、$${c}$$が飛び地と飛び地を繋ぐ線の上にあるときは$${z_n}$$は実軸上を非周期的にうろつく挙動になるようです。(飛び地の中にある場合はちゃんと周期的になってくれます)


これらの選手の記録($${\infty}$$周期)をランキングに含めると、当然ながら1位を占拠してしまって面白くないので除外することにしています。
ちなみに、それぞれの例に対応するジュリア集合は以下のようになります。


-1.6のような「線の上パターン」の値は、ジュリア集合を描画してみると収束領域が無く枝状の線だけでできたジュリア集合になります。
特定の$${c}$$の値に対してジュリア集合の周期が無限かどうかをコンピュータによる計算だけで判断するのは(私の技術力では)困難ですが、ジュリア集合を描画してみてその形状を観察することでほぼほぼ正確に判断できるのではないかと思っています。
すみません、前提知識の説明だけでアドベントカレンダーの他の日の1日分くらいの文章量になってしまいましたが、ここからようやく本編である第3回高周期ジュリア集合選手権を開催いたします。
選りすぐりの複素数たちによる美しきジュリア集合の数々をお楽しみください。
c(z^5-1)

本大会最初の競技は、$${c(z^5-1)}$$です。
前回までは、第$${n}$$回大会の第1競技として$${z^{n+2}+c}$$という形の関数を選んでいました。
なので今回も$${z^5+c}$$を第1競技にしたかったのですが、1つ懸念点がありました。
それは、参加条件がやたら厳しくなってしまうことです。

ご覧のように$${z^5+c}$$のマンデルブロ集合は非常に対称性が高い形をしており、被りの除外をすると参加条件の範囲は上の図の$${\frac{1}{32}}$$の範囲(0≤y≤x≤1)に絞られてしまいます。
参加条件が狭いと、大きい記録が出ず競技が盛り上がらない可能性が高いため、代わりに$${c(z^5-1)}$$を第1競技とすることになりました。
$${c(z^5-1)}$$であれば、「実部と虚部の小数点以下が2桁」の複素数がなす格子の対称軸と一致するような対称軸は1本(実軸)しかないため、$${z^5+c}$$よりも間口の広い競技とすることができます。
というわけで、この競技の参加条件は「実部と虚部の小数点以下は2桁まで、実部は-2~1、虚部は0~2」とします。
5位:0.8+0.28i(46周期)

星空のように淡くきらめく0.8+0.28iが、46周期で5位にランクイン。
$${c(z^5-1)}$$が$${z^5+c}$$の代わりとして選ばれた理由には、「ジュリア集合の形がそっくりだから」というのもあります。

計算上では、$${z^5+c}$$と$${(-c)^{\frac{4}{5}}(z^5-1)}$$は同じ形(相似)のジュリア集合を生成するっぽいです。
4位:0.13+0.72i(56周期)

56周期の0.13+0.72iが4位にランクイン。
先程の0.8+0.28iと全く同じ暗い青系の彩色関数を使用していますが、0.8+0.28iとは異なり宇宙というよりかはどこか有機的で、海を連想させるような配色になりました。
3位:-0.86+0.07i(70周期)

下位2名とは打って変わり、カラフルでありながら禍々しさを併せ持つ-0.86+0.77iが70周期で3位にランクイン。
中央や周りに五芒星っぽい領域が見られますが、どうやらこの性質は$${f(z,c)}$$の臨界点の多重度と関係があるようです。
※この先の説明は感覚と経験則による非数学的な記述を含みます。
$${c(z^5-1)}$$の臨界点を求めるための方程式は$${5cz^4=0}$$という4次方程式ですが、この方程式の解$${z=0}$$は4重解です。
一般に、$${c(z^n-1)}$$の臨界点は$${n-1}$$重解になっており、$${c(z^n-1)}$$のジュリア集合は$${n}$$角形っぽい領域を持ちます。

また、$${z^5+z^4+c}$$の臨界点は$${-\frac{4}{5}}$$と3重解の0なので、3重解に対応する四角い領域と$${z^2+c}$$のジュリア集合のような1重解の領域が同時に出現することがあります。

(白い領域がz_0=-4/5のサイクルに収束する領域、その他のカラフルな領域がz_0=0に対応する領域)
今回の記事では触れませんが、臨界点が0でない場合や$${f(z,c)}$$が超越関数の場合(この場合は導関数の零点の位数)などでも同様に、臨界点の多重度に応じてジュリア集合に「$${c(z^n-1)}$$や$${z^n+c}$$のジュリア集合に似た形」が現れる現象が見られます。
なお、繰り返しになりますが、これらの説明はジュリア集合の見た目に対する感覚的な観察結果と数学的な裏付けを持たない経験則を述べただけのものであることに注意してください。
2位:0.42+0.67i(111周期)

0.42+0.67iが111周期で2位にランクイン。
「2位で初めて100周期を超える」という展開になった競技は第0回大会から数えると6例目になり、割合でいうと12競技中6回なのでちょうど半分が該当しています。
競技の選別が無作為ではない(参加条件が広すぎたり狭すぎたりすると面白くないのでちょうどいいものを選んでいる)とはいえ、共通点のある試合がこう何度も発生するのは不思議な気がします。
1位:-0.33+0.77i(2805周期)

1位の座に輝いたのは、2805周期の-0.33+0.77i。
2位の25倍を超える大記録による勝利となりました。
c(z^2/2+1/z)

続いての競技は、$${c(\frac{z^2}{2}+\frac{1}{z})}$$です。
3回回転対称なマンデルブロ集合が特徴的ですが、どうやらジュリア集合も3回回転対称になるようです。

一般に、$${c_1(c_2z^m-c_3z^n)}$$という形の関数のジュリア集合は$${|m-n|}$$回回転対称になるようです。
ちなみに、これまでに実施してきた競技のうち$${c_1(c_2z^m-c_3z^n)}$$の形をしているものは以下の通りです。

※実施済み競技に該当するものが無いので分かりにくいですが、$${m-n}$$が負の場合でもジュリア集合はちゃんと$${|m-n|}$$回回転対称になります。
また、$${c(\frac{z^2}{2}+\frac{1}{z})}$$は臨界点を3つ($${1}$$、$${\frac{-1+\sqrt{3}i}{2}}$$、$${\frac{-1-\sqrt{3}i}{2}}$$)持つのも特徴的です。
しかし、どの初期値でも全く同じ形のマンデルブロ集合が生成される(≒初期値を変えても競技結果はあまり変わらなそう)ので、今回は$${z_0=1}$$のときの周期のみを記録として扱います。
なお、前回大会までは「臨界点が二つ存在して片方のみを集計対象とする場合、集計対象外の臨界点に対応するサイクルに収束する領域は白で塗る」というルールでジュリア集合を描画していました。

今回は集計対象外の初期値が2つあるので、$${\frac{-1+\sqrt{3}i}{2}}$$に対応する領域は青、$${\frac{-1-\sqrt{3}i}{2}}$$は白で彩色することにしました。
5位:-0.67+0.59i(78周期)

78周期の-0.67+0.59iが5位にランクイン。
「臨界点が3個でジュリア集合が3回回転対称」とのことなので、各臨界点に対応する同じ形の収束領域が3回回転対称に並ぶと予想していたのですが、どうやら違うようです。

4位:-0.75+0.35i(90周期)

-0.75+0.35iが、90周期で4位にランクイン。
3位:0.06+0.11i(94周期)

0.06+0.11iが、94周期で3位にランクイン。
上の画像は実部と虚部が-2から2までの範囲を映したものですが、このジュリア集合はもっと外側の範囲まで収束領域が広がっています。

一般に、$${cf(z)}$$という形の関数のジュリア集合は$${c}$$の絶対値が小さいほどサイズが大きくなる傾向があります。
2位:-0.5+0.13i(142周期)

-0.5+0.13iが142周期で2位にランクイン。
本大会2度目の「2位で初の100越え」が出ました。
1位:-1.05+0.18i(444周期)

1位を勝ち取ったのは、網目模様の美しい-1.05+0.18i(444周期)。
網目模様は多項式関数では(多分)見られない分数関数の特徴ですが、関数やパラメータの違いで大きく印象が変わるのが面白いですね。
ところで、今回のランキングでは青い領域($${\frac{-1+\sqrt{3}i}{2}}$$に対応する領域)のあるジュリア集合が全く出てこなかったのが不思議ですね。
描画プログラムの仕様上$${z_0=1}$$と$${z_0=\frac{-1+\sqrt{3}i}{2}}$$のときの数列が同じサイクルに収束すると青い領域が出現しなくなるのですが、6位以下では普通に青い領域が見られたのでTOP5に1個も入らないのは謎です。
あとこれはめちゃくちゃどうでもいいことですが、444って不吉で嫌ですね。
c(z^3/3-z^2)+2

続いての競技は、$${c(\frac{z^3}{3}-z^2)+2}$$です。
$${c(\frac{z^3}{3}-z^2)+2}$$は3次関数なので最大で2個の臨界点を持つ可能性があり、実際に計算してみると$${z=0}$$と$${z=2}$$の2つの臨界点があることがわかります。
前回大会まででは、臨界点が複数存在する競技に対しては
何かしらの数学的な理由により、1個の臨界点に対応する周期のみを記録として扱う
特に理由もなく、1個の臨界点に対応する周期のみを記録として扱う
「チーム戦」と称して全ての臨界値に対応する記録を集計する
などの対応をとっていました。
今回のケースでは、$${f(0,c)=c(\frac{0^3}{3}-0^2)+2=2}$$が成り立つので、$${z_0=0}$$でも$${z_0=2}$$でも全く同じジュリア集合ができる(もちろん記録も同じ)ことがわかります。
つまり初期値は実質1個しか無いので、$${z_0=2}$$による周期のみを記録として集計することとし、参加条件は「実部と虚部の小数点以下は2桁まで、実部は-2~3、虚部は0~2」としました。
ちなみにこんな感じで「臨界点が実質1個しかないと見做せる3次関数」は他にもたくさんあって、例えば0と1が臨界点である場合は
$${f(0,c)=0}$$:$${f(z,c)=c(2z^3-3z^2)}$$
$${f(f(0,c),0)=0}$$:$${f(z,c)=-\frac{1}{2c^2-3c}(2z^3-3z^2)+c}$$
$${f(f(0,c),c)=f(0,c)}$$:$${f(z,c)=c(2z^3-3z^2)+\frac{3}{2}}$$
$${f(1,c)=1}$$:$${f(z,c)=c(2z^3-3z^2+1)+1}$$
$${f(f(1,c),c)=f(1,c)}$$:$${f(z,c)=c(2z^3-3z^2+1)-\frac{1}{2}}$$
$${f(1,c)=0}$$:$${f(z,c)=c(2z^3-3z^2+1)}$$
$${f(0,c)=1}$$:$${f(z,c)=c(2z^3-3z^2)+1}$$
$${f(f(0,c),c)=f(1,c)}$$:$${f(z,c)=c(2z^3-3z^2+1)+\frac{3}{2}}$$
$${f(f(1,c),c)=f(0,c)}$$:$${f(z,c)=c(2z^3-3z^2)-\frac{1}{2}}$$
・・・等があります。
5位:1.81+0.02i(138周期)

1.81+0.02iが、138周期で5位にランクイン。
このジュリア集合の見た目は、$${c(z^5-1)}$$のランキング中で触れた「3重臨界点を持つ多項式関数のジュリア集合」の特徴と合致しています。
しかし、$${c(\frac{z^3}{3}-z^2)+2}$$は3次関数なので臨界点の多重度が3になることはありえないはずです。
じゃあどういうことなのかというと、どうやら$${f(z,c)}$$は3重臨界点を持たないものの$${f(f(z,c),c)}$$の臨界点が3重になっているようです。
グラフ描画ツールで確認してみると、$${f(f(x,c),c)}$$のグラフの$${x=0}$$の周りの形状は$${y=x^4}$$の$${x=0}$$(3重臨界点)の周りのように潰れた形になっています。


詳細は不明ですが、おそらくこの性質によって3重臨界点を持たないにもかかわらず3重っぽいジュリア集合が生成されるのだと思います。
4位:0.48+0.75i(180周期)

180周期の0.48+0.75iが、4位にランクイン。
左側の卍型の領域は$${z^4+c}$$のジュリア集合に、右側のZ型の部分は$${z^2+c}$$のジュリア集合に似ています。
このように4次関数と2次関数が混ざったような形のジュリア集合は、多項式関数では$${z^5+z^4+c}$$のような5次以上の関数でしか見られないと思っていたので、この関数の発見は個人的にはかなり衝撃的でした。
3位:1.96(242周期)

242周期の1.96が3位に・・・と言いたいところですが、この判定には疑問の余地があります。
まず、上の画像には収束領域が映っていません。
また、マンデルブロ集合上で確認すると、1.96は右側の飛び地の間の線の上にあるように見えます。

なお、ジュリア集合の方の原点付近を拡大してみたところ、計算精度に問題があるのか以下のように正常に描画できず、収束領域の存在は確認できませんでした。

以上を踏まえると、$${1.96(\frac{z^3}{3}-z^2)+2}$$は以下のどれかに該当すると考えられます。
有限の周期を持つが、収束領域は小さすぎて確認不能である(大会の運営・審査体制に問題あり)
有限の周期を持つが、収束領域はない(同上)
無限周期である(失格&誤審)
いずれにせよ、大会の大前提を揺るがしかねない大問題に直面してしまっているようです。
ただ、審査の雑さが問題(Processingによる計算+Excellグラフ目視)なのは明らかですが、センサー内蔵ボールのように正確無比な判定法が見つかるとは正直思えないです。
とりあえず、今回は1.96を242周期で3位とする判定は変更しないでおこうと思います。

ちなみに、$${1.96(\frac{z^3}{3}-z^2)+2}$$が242周期の吸引サイクルを持つかどうかを厳密に判定する方法は存在するのですが、29063214161986986067637023528620257232321357468243916695175073145996989031241146647825183302277227705597018408555209(=3²⁴²)次方程式を解く必要があるため、現実的ではありません。
追記:少し検証してみたところ、どうやら$${1.96(\frac{z^3}{3}-z^2)+2}$$は本当は$${\infty}$$周期っぽいです。
2位:0.81+0.53i(396周期)

細やかな樹枝状構造と渦巻きの組み合わせが美しい0.81+0.53iが、396周期で2位にランクイン。
1位:0.65+0.65i(434周期)

栄えある第1位は、434周期の0.65+0.65i。
2位の0.81+0.53iと似た形のジュリア集合となり、競技の締めくくりとしてはイマイチ盛り上がりに欠ける展開となってしまいましたが、競技自体は完全に想定外の展開が2度も起きる大変刺激的なものとなりました。
z^3/(z+0.1i)+c

今大会4つ目の競技は、$${\frac{z^3}{z+0.1i}+c}$$です。
マンデルブロ集合の見た目は$${z^2+c}$$のものと似ていますが、よく見ると細部の形が違います。



また、上下方向の対称性が無いのも特徴的ですが、これは分母にある$${0.1i}$$のせいで$${f(\text{con}(z),\text{con}(c))=\text{con}(f(z,c))}$$という性質が崩れているためです。($${\text{con}(z)}$$は$${z}$$の複素共役)
対称性が無いという事は結果被りも生じないので、参加条件は「実部と虚部の小数点以下は2桁まで、実部は-2~1、虚部は-2~2」とし、初期値は0としました。(0のほかに-0.15iも臨界点ですが、結果が面白くなさそうだったので無視します)
5位:-0.18-0.78i(120周期)

120周期の-0.18-0.78iが5位にランクイン。
虚部が負であるような選手は今までずっと参加を制限されてきましたが、ようやく日の目を見ることとなりました。
4位:-0.48-0.47i(125周期)

ギラギラで派手派手な-0.48-0.47iが、125周期で4位にランクイン。
このジュリア集合は、奇抜な配色以外にも珍しい(主観)特徴を持っています。
説明しやすくするために、一旦別のジュリア集合を出します。

まず、これは$${z^2+0.37+0.15i}$$のジュリア集合です。
$${z_n}$$の周期サイクルを図示すると以下のようになります。

サイクルを構成する7個は環状に並び、それぞれの点は別々の収束領域に属し、その収束領域は環の中央の1点でつながっています。
今まで紹介してきたジュリア集合でも、「サイクルを構成する点が環状に並び、その中央で収束領域が1点に集まっている」という形をしたものがいくつかありました。

ところが、$${\frac{z^3}{z+0.1i}-0.48-0.47i}$$のジュリア集合は違います。

サイクルを構成する点は環状になっているものの、それらの点を含む収束領域は1点に集まらず収束領域自体が環状に繋がっており、その環の中には別の初期値の収束領域があります。
このような特徴を持ったジュリア集合は、今大会どころか過去の大会でも一切登場例が無く、感覚的には非常に珍しいように感じます。
3位:0.38+0.29i(126周期)

0.38+0.29iが126周期で3位にランクイン。
$${\frac{z^3}{z+0.1i}+c}$$の$${z=0}$$の臨界点は2重臨界点になっているので、収束領域が$${z^3+c}$$のジュリア集合のような三角形っぽい形になることがあります。
2位:-0.48+0.64i(130周期)

130周期の-0.48+0.64iが2位にランクイン。
5位が120周期でその上は125、126、130という並びとなり、狭い範囲に4名の選手がひしめく接戦となっています。
1位:-0.22-0.75i(225周期)

激戦を制したのは、225周期の-0.22-0.75i。
僅差の記録が続いた2位以下に対して大差での勝利となりました。
con(z)^3/3-con(z)^2/2+c
今大会最後の競技は、$${\frac{\text{con}(z)^3}{3}-\frac{\text{con}(z)^2}{2}+c}$$です。($${\text{con}(z)}$$は複素共役)



$${\frac{\text{con}(z)^3}{3}-\frac{\text{con}(z)^2}{2}+c}$$は微分不可能らしいのですが、どうやら$${\frac{z^3}{3}-\frac{z^2}{2}+c}$$の臨界点と同じ0と1を初期値にすることで「ジュリア集合の性質が反映されたマンデルブロ集合」を描画できるようです。
さて、この競技は(臨界点に相当する)初期値が二つ存在し、少し調べたところ初期値によって競技の結果も変わりそうでした。
というわけで、この競技では$${c}$$の値と初期値の組を1名の選手と見做し、チーム対抗戦として$${z_0=0}$$チームと$${z_0=1}$$チームの2陣営に1位の座を奪い合っていただきます。(総合得点とかによる勝敗はなく、1位を取った選手の所属するチームが勝ちです)
前回大会でも0 vs 1によるチーム戦を実施したので、今回は実質リベンジマッチに相当します。
参加条件は、両チームとも「実部と虚部の小数点以下は2桁まで、実部は-2~3、虚部は0~2」とします。
5位:(0,1.57+0.86i),(1,1.57+0.86i) (148周期)

両チームの1.57+0.86iが、148周期で同率5位にランクイン。
4位:(0,-0.48+1.17i),(1,-0.48+1.17i) (180周期)

両チームの-0.48+1.17iが、180周期で4位にランクイン。
両者一歩も譲らない展開が続きます。
3位:(0,-0.34+0.64i),(1,-0.34+0.64i) (242周期)

またしても両チームの-0.34+0.64iが、242周期で同率3位にランクイン。
所々に見られる向かい合った渦巻きが、まるで互いに睨み合う両チームを表しているようです。
2位:(0,-0.32+0.67i) (300周期)

ガラス細工のような繊細な美しさを持つ0チームの-0.32+0.67iが、300周期で2位にランクイン。
3位までの均衡を打ち破り、単独でのランクインとなりました。
1位:(1,-0.36+0.67i) (1080周期)

有終の美を飾ったのは、1チームの-0.36+0.67i(1080周期)。
2位以下に大差をつけ、見事に前回大会の雪辱(?)を果たしました。
最後に
今大会の競技は以上となります。
ここまで読んでいただき(または画像を流し見していただき)ありがとうございました。
それでは、さようなら。
日曜数学 Advent Calendar 2022の明日の記事は、icqk3さんによる微分ガロア理論の記事です。
おまけ
ランキング外だったけど面白かったジュリア集合や、競技結果と直接は関係ないけど面白かった画像などを載せます。


冒頭の説明に出てきた「$${c}$$がマンデルブロ集合のフチにあるパターン」の無限周期ジュリア集合です。
もう一つの方の無限周期パターンに比べるとかなりレアで、他の3つの競技では確認できませんでした。


私は元々こういう見た目のジュリア集合が好きで、第0回大会(の元になった調査)は「いい感じの見た目のジュリア集合を生成できるキリのいいパラメータを見つけたい」という動機により始めたのでした。



$${c(\frac{z^2}{2}+\frac{1}{z})}$$のルール説明では「$${\frac{-1+\sqrt{3}i}{2}}$$に対応する領域は青で塗る」なんて言うルールを作っておきながら、結局ランキングでは青領域のあるジュリア集合は1個も出てきませんでした。
ランキング外でならこのように3つの初期値がそれぞれ別のサイクルに収束するようなパラメータもあったのですが、ジュリア集合の形も初期値の配置も3回回転対称なのにサイクル自体は全然3回回転対称にならないのが非自明で面白いですね。


$${c(\frac{z^2}{2}+\frac{1}{z})}$$の項目で少し触れた「$${c_1(c_2z^m-c_3z^n)}$$の$${|m-n|}$$が負になる関数」の実例です。


「面白くなさそうだから」と雑にあしらった、$${\frac{z^3}{z+0.1i}+c}$$のもう一つの臨界点を使ったマンデルブロ集合です。


ランキング入りはしなかったものの、$${\frac{\text{con}(z)^3}{3}-\frac{\text{con}(z)^2}{2}+c}$$のジュリア集合には$${\frac{z^3}{3}-\frac{z^2}{2}+c}$$と同じように2つの初期値から別々のサイクルが生成されたり変な領域が存在したりするジュリア集合が見られました。
※☟「変な領域」という単語についてはこの記事で説明(?)しています。









地味なジュリア集合ばかりTOP5入りしてしまいましたが、$${\frac{z^3}{z+0.1i}+c}$$のジュリア集合は変わった形のものが多くてめちゃくちゃ面白いです。






没競技です。
$${\frac{z^3}{z+0.1i}+c}$$と同じように収束領域が環状に並んだりするのが面白いと思っていたのですが、$${\frac{z^3}{z+0.1i}+c}$$の方が面白いと判断して没になりました。
