慶應義塾大学2020商学部 数学 大問４ 立体図形

お世話になります。ドリームラーナーズの石原です。鳥取県倉吉市で進路指導と学習法指導の塾を運営しています。学習指導は中学生・高校生・大人、英語の指導は小学生から対応しています。LINEなどを活用して、遠隔地でも進路指導・学習指導に対応しています。

今日は過去問解説にチャレンジします。慶應義塾大学商学部の数学です。問題本体は載せませんので、ご自分で用意してください。

なるべく「与えられた問題文をどう読むか、読んで何を考えるか」と言う点を重点的に解説していきたいと思います。あと、「いかに簡単に、楽して解くか」も重視します。数式を試行錯誤してぐちゃぐちゃやって解けた、と言う話はあまり参考にならないと思いますし。載せているのは考え方だけです。私が普段やっている指導では、これを小出しにしながら誘導していくスタイルを取っています。

多分、クソ真面目に全部やりがちで遅くて間に合わねえ！もっと時間かけたい問題に時間かけられねえじゃねえか！という人にはうってつけの解説かと思います。

大問４：状況整理

立体図形って、ビビる人多いんですよ。なぜかって、「立体で図が描けない」とか思うからなんですけど、この問題は、状況から判断して「立体で図」を書く必要がありません。

本文にはこう書いてあります。

z軸上の点Hを通る平面のうち、
zx平面上の点Aで球面Sと接する平面α
yz平面上の点Bで球面Sと接する平面β

これをこのように情報を追加して、訳していきます。

z軸上の点Hを通る平面のうち、
zx平面上（y座標が0）の点Aで球面Sと接する平面α
（球の対称性から、zx平面で切ると、直線に見える）
yz平面上（x座標が0）の点Bで球面Sと接する平面β
（球の対称性から、yz平面で切ると、直線に見える）

平面αから検証しますが、どっちにしろ対称性から平面βも同じになります。

zx平面が球と接しているということは、zx平面で切ると、平面αはこうやって直線に見えます。直線を書くと見づらくなるので、HH'で切っていますが、直線HH'が平面αであると考えてください。

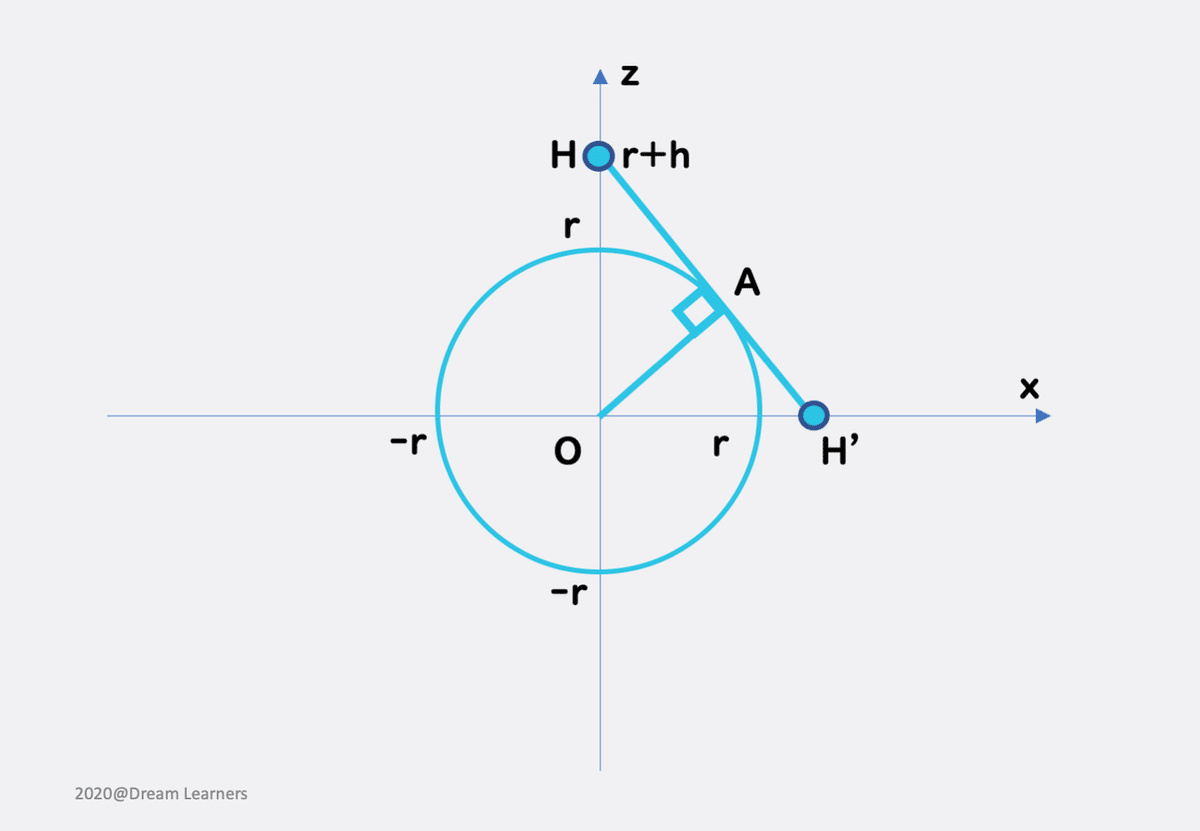
これがわかれば、この問題はあとはやるだけです。進めましょう。

大問４（ⅰ）：点Aの座標

これは相似で考えたら良いでしょう。以下のように、直角三角形に目をつけて相似を見抜いて、角度のsin値だけスッパぬいて点Aの座標を求めます。

大問４（ⅱ）：平面αの方程式

この平面α、前提の図で見えているのはy=0の場合なのですが、これがyがいくらになっても、この方向（y軸の正方向）から見た場合、常に同じ直線でxz平面に現れます。球の原点対称性から、そこが同じでなければxz平面で接していないことになってしまいます。

なので、yが関係ないですから、図で見えてるxz平面での直線の方程式が、そのまま平面αの方程式になります。

上図のθを流用します。直線HH'の傾きは、直線OAの傾きtanθと垂直ですから、欲しい傾きから求めると、

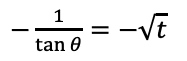
この直線は点Aを通るので、

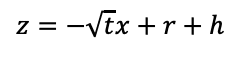
条件から、解答にはrやhを使ってはいけないので、空欄の形に合わせると

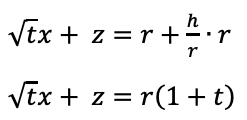
これが求める方程式です。

大問４（ⅲ）：角度？いや、ベクトルで簡単に…

平面βも平面αに倣って図示すると、まとめて以下のようになります。

まず平面α（y座標は0です）。ベクトルOAは、平面αに対する法線ベクトルの１つであることがわかります。

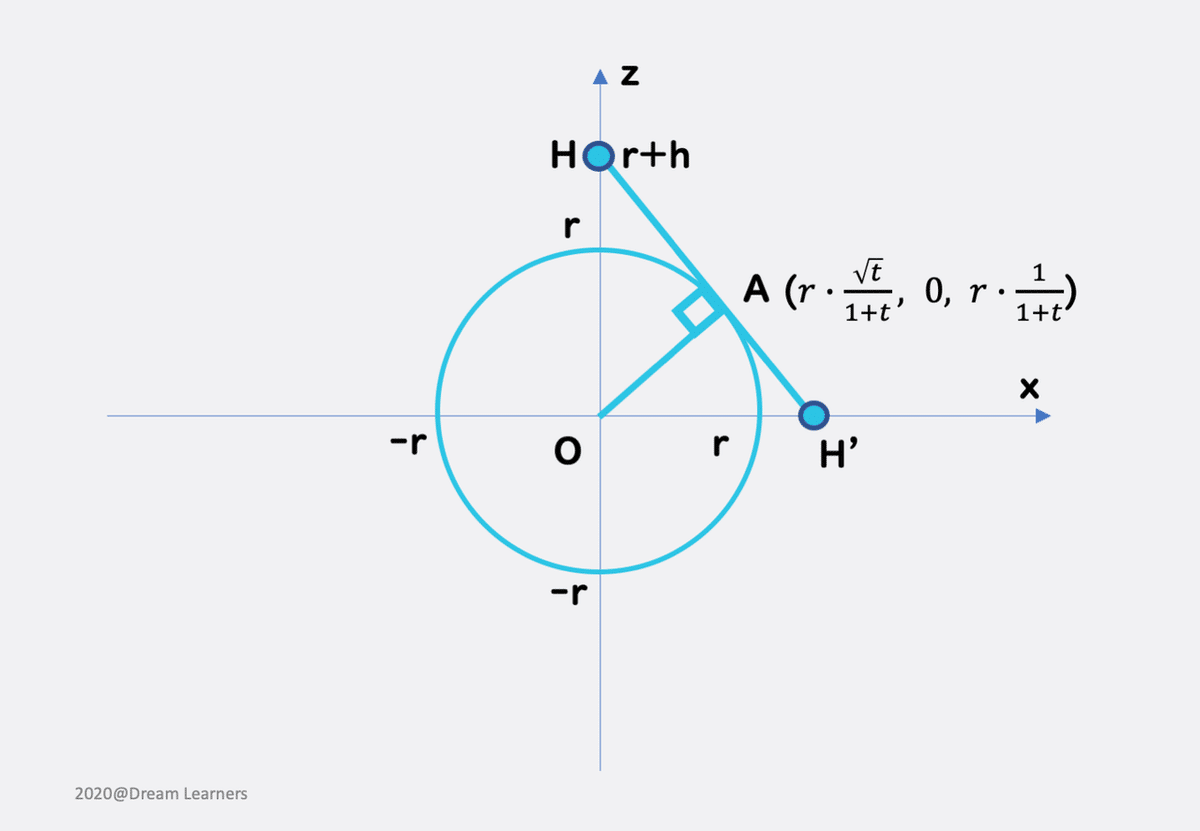
次に平面β（x座標は0です）。ベクトルOBは、平面βに対する法線ベクトルの１つであることがわかります。

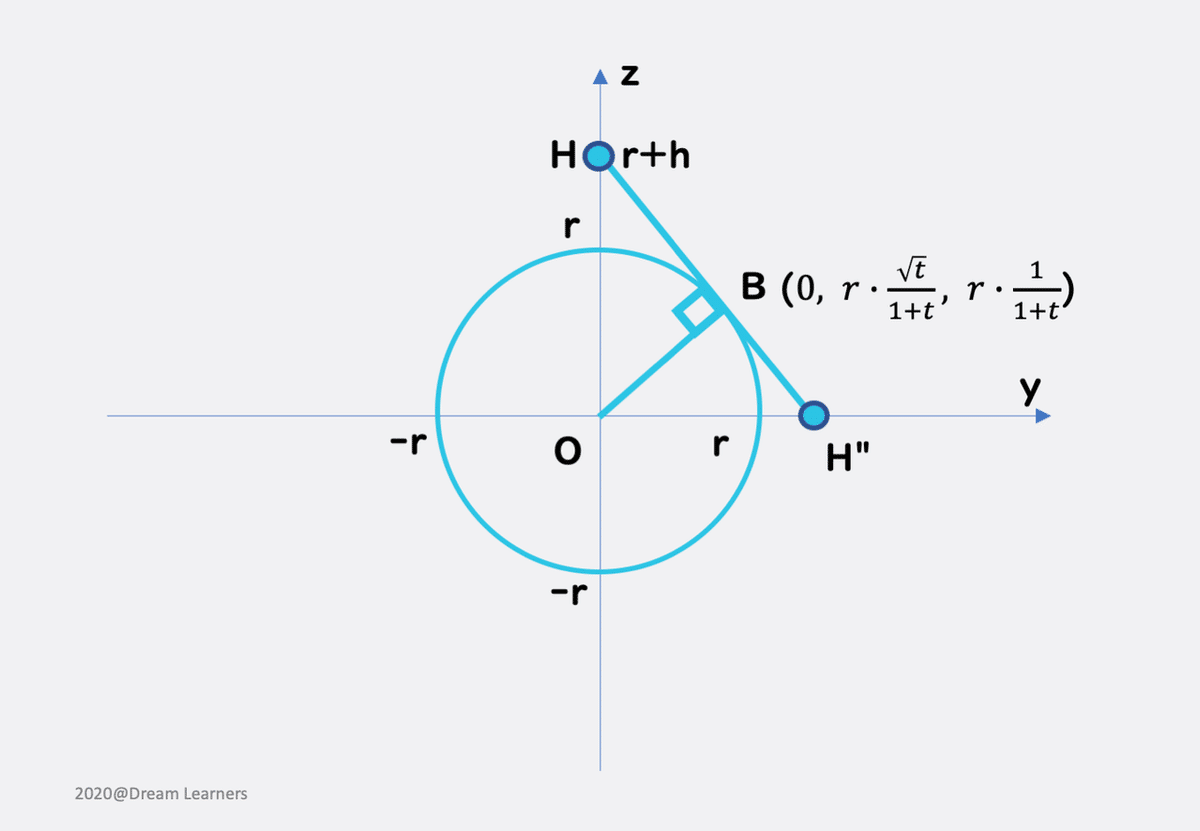
ということで、それぞれ法線ベクトルって、OA、OBのことなので、これを使って、角度を求められます。都合よくゼロがあるので、式は簡単になりますね。

大問４（ⅳ）：θの近似値を三角比表から求める

あとは流れ作業だとは思いますが…

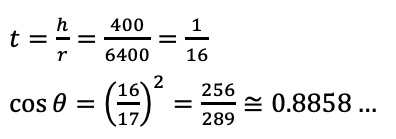
16の二乗とか、17の二乗とか出ていますが、どちらもせいぜい3桁なので、心配せずまず二乗値を計算してから、出してやりましょう。これを表から見て、「近い方」を探せと指示がありますから、探すと、θ＝28°です。

本日は以上です。難易度は、これ自体は例年並みでしょう。平面で書けることに気づけば早いですし、計算も大したものではありません。しかし、他の問題と見比べたときに、難しく見えて優先度が下がるので、当日のセットで考えたらこれは難しい方、つまり、完答できた人が少ない方になるかもしれません。

難関大志望者の中で勝ち残る学習法を公式ウェブサイトで公開中！
LINEやSkypeによる無料相談も受付中！

【初回相談無料】ドリームラーナーズ