20000320　球の裏返し

　球面を裏返すことが出来るか。普通はできない。穴のないゴムボールを裏返すことはMr.マリック$${^{*1}}$$でもなかなかできない。穴が開いたボールならその穴を広げれば靴下を裏返すようにボールを裏返すことができる。しかし穴が一つもなければ無理である。

　そこでボールの皮はいくらでも伸びて、しかも皮の厚さは無限に薄く、その皮はお互いにすり抜けることができるとする。これで裏返すことができるかどうかが議論できるようになる。ただし切り貼りは御法度とする。

　1956年にスメールが裏返すことができることを証明した。

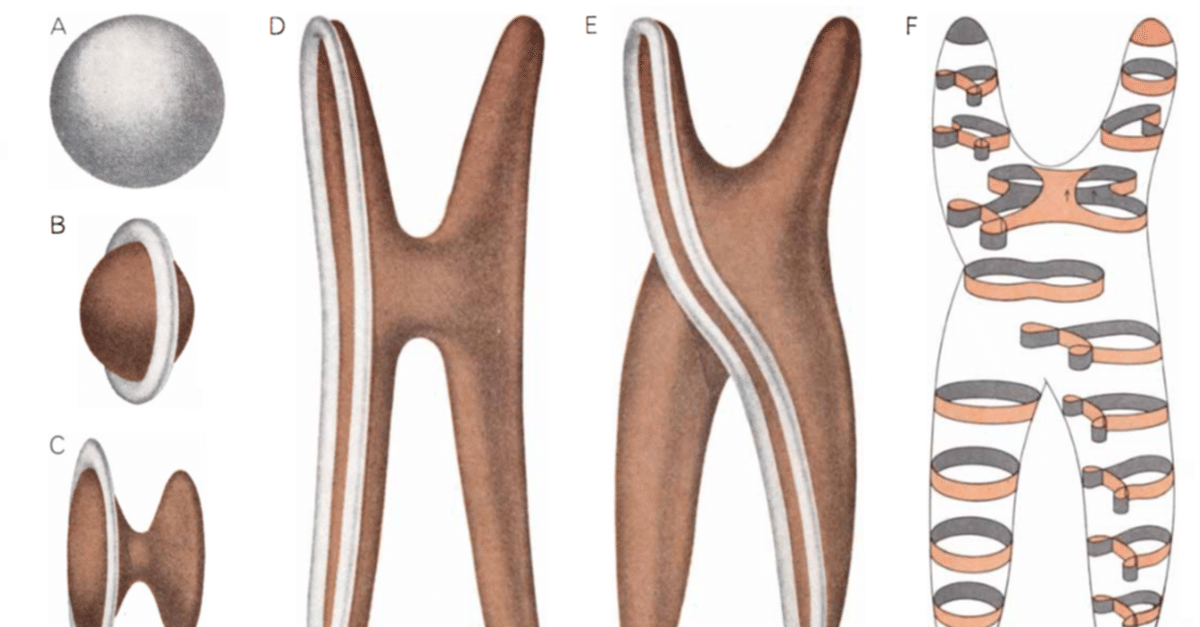
　ゴムボールを地球に見立てて考えてみる。この地球は地表だけの中身が詰まっていない状態である。地球の北極と南極を近づけるようにして潰していく。北極と南極とがぶつかって、極の部分の皮は互いに通り抜け、南極の裏側と北極の裏側が出てくる。通り抜けた裏南極と裏北極を更にお互い反対方向に引張ると、裏返った地球の赤道に丁度ドーナツを巻き付けたような形$${^{*2}}$$ができる。この赤道のドーナツの皮は表側のままである。このドーナツの周辺の皮を引張ればいくらでもドーナツを細くできるのだが、どうしても皮は表側のままで残る。ドーナツを切り離し、裏返して貼り付ければ裏返しは完了する。しかし今考えている地球ボールの皮は切ったり貼ったりができないことになっている。従ってこのままでは滑らかに球面を裏返す事ができない。

　スメールが球の裏返しが可能であることを証明できたと報告した時、彼の指導教授は上記のような直感で彼の証明が間違っていると指摘した。
　もともとスメールの論文は「空間E3に埋め込まれた相異なる向きを持つ球面S2は互いに正則ホモトープである」ということを証明したに過ぎない。この証明は球面を裏返す事ができるという意味にもなるらしいが、その方法を示した訳ではなかったので、スメールは具体的な裏返し方法を明示できなかった。

　後に別の人$${^{*3}}$$がこの裏返す方法を示した。これ$${^{*4}}$$を見た時、裏返す様子$${^{*5}}$$をコンピュータグラフィックで作ってみたいと思っていた。世界には同じようなことを考える人が必ずいるようだ。

　ここ$${^{*6}}$$にあった。

*1　Mr.Maric's Home Page
*2　http://www.geom.umn.edu/docs/outreach/oi/Frames/ring.gif
*3　Outside In: A brief history of sphere eversions
*4　http://www.geom.umn.edu/docs/outreach/oi/Frames/phillips.gif
*5　Outside In: The Script of Outside In
*6　Outside In: Movie Clips and Interactive Graphics