
どんな数にも魔法をかけてご覧いれます〜魔方陣を作るまでの道のり②(1次、2次、3次)
1 はじめに
魔方陣とは、縦・横・斜めの数を足すと、すべて同じ数になる数の並びです。

前回の記事では、$${n}$$次魔方陣($${n×n}$$の表)の縦・横・斜めの数の和(定和)は、
$${\frac{1}{2}n(n^2+1)}$$
という性質を導けました。
例えば、上の図のように4次魔方陣(4×4の表)だと
$${\frac{1}{2}×4×(4^2+1)=34}$$
というように計算でわかる。
では、この定和の性質という武器と$${4k}$$次魔方陣は作れるという武器を使って、$${n}$$次魔方陣を作るアルゴリズムを見つける長~~い旅に出発したいと思います。

2 1次魔方陣は自明
1次魔方陣は、次のようなものです。
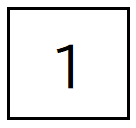
1次魔方陣の定和は、
$${\frac{1}{2}×1×(1^2+1)=1}$$
です。ただ、1次魔方陣は表のマスは1個しかないし、1しか書かれていないから上の図の魔方陣で完成です。自明です。
3 2次魔方陣は・・・
2次魔方陣は表に1~4の数が書かれています。定和は、
$${\frac{1}{2}×2×(2^2+1)=5}$$
です。
魔方陣になる前は、下のような表です。

さて、斜めの和は5(=定和)です。しかし、「2」と「3」を動かしても縦と横の和で5を作ることができません。
よって、2次魔方陣は作ることができません。
4 3次魔方陣は・・・
2次魔方陣は表に1~9の数が書かれています。定和は、
$${\frac{1}{2}×3×(3^2+1)=15}$$
です。
魔方陣になる前は、下のような表です。

では、魔方陣を作っていきます。
・ 2行2列のマスを埋める
最初にどのマスから埋めるか考えると、2行2列のマスがいいと考えました。理由は、3次魔方陣の場合は定和15を作らないといけない3つの数の組み合わせは8通りあります。その8通りの中で2行2列のマスは、4つの和に関わっています。そのため、2行2列のマスから埋めたほうがいいと考えました。

2行2列のマス以外に入る数を、$${a}$$~$${h}$$とします。2行2列のマスに入る数を$${x}$$とします。

2つ前の図の②、⑤、⑦、⑧の和はそれぞれ15なので、
$${(b+x+h)+(d+x+e)+(a+x+i)+(c+x+f)=15×4}$$
$${(a+b+c+d+x+e+f+g+h)+3x=60}$$
$${a+b+c+d+x+e+f+g+h=45}$$だから、
$${45+3x=60}$$
$${3x=15}$$
$${x=5}$$
よって、2行2列のマスは5です。

・ 「9」をどのマスに入れる?
次に「9」をどこに入れるか決めます。なぜ「9」なのかというと、縦・横・斜めの和が15になるようにするとき、大きい数であればあるほど制約が大きくなるからです。
・ 「9」を四隅のマスに入れた場合
では、例えば「9」を3行3列のマスに入れたとします。そうすると、1行1列は「1」で決まりです。では、次に3行目と3列目の和が15になるように4マスを埋めます。2数の和が「6」になる組を、残りの2,3,4,6,7,8から作ればいいです。しかしそのような2数の組は、{2,4}の1組しか作れません。よって、「9」を3行3列のマスに入れたことが間違いだったのです。

このことから、「9」は四隅に入れることができないこともわかります。
よって「9」を、2行3列のマスに入れます。すると、2行1列のマスは「1」で決定です。

・ 「8」をどこに入れる?
次に「8」を入れるマスはどこか考えます。ここで、先ほど書いた「大きい数であればあるほど制約が大きくなる」という意味がわかっていただけると思います。定和が15なので、1行3列と3行3列のマスには書けません。

では、「8」を1行2列のマスに書きます。そうすると、3行2列のマスは「2」で決まりです。
残ったのは3、4、6、7です。ただ、9が2行2列のマスにあるため、1行3列と3行3列のマスには6,7は入れられないため、3と4が入ります。ここで3列目の和が16となってしまいます。

よって、「8」を入れるマスは1行2列のマスではないと言えます。同様に3行2列、1行3列と3行3列のマスでもないです。このことから、「8」は1行1列のマスに書きます。自動的に3行3列のマスは「2」で決まり!また3行1列のマスは「6」で決定です。関連して、1行3列、3行3列、1行2列、3行2列のマスはそれぞれ「4」と「2」と「3」と「7」です。
これで魔方陣の完成です。

5 3次魔方陣は1通りしかないのだろうか?
3次魔方陣は1通りではありません。「5」は2行2列のマスに書くことは決まっていて、その次に「9」を書くマスは4通りあります。その「9」を書くマスの位置によって、「8」を書くマスは2通りあります。よって、3次魔方陣は8通りあります。


しかし、この8通りの魔方陣を書いて分かりましたが、回転したり、対称移動したりすると、1通りしかないことが分かります。
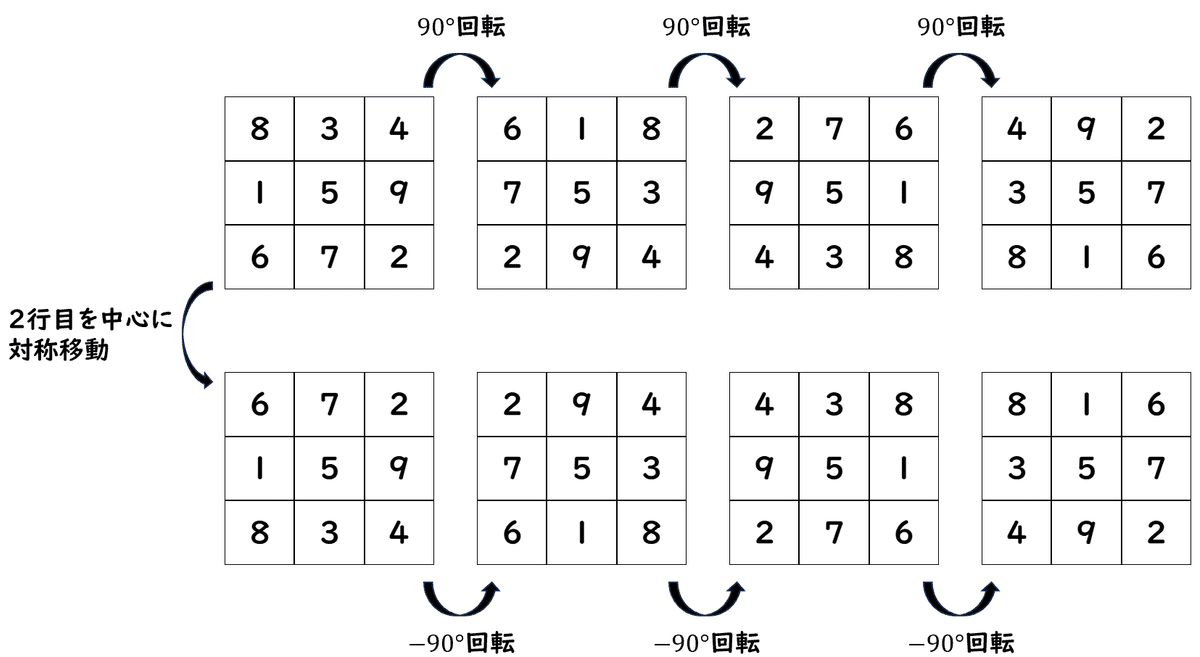
回転したり、対称移動したりして重なるなら、同じ魔方陣とみなすとすれば、3次魔方陣は1通りしかありません。
6 おわりに
今回は、1~3次魔方陣について考え、作ることができました。しかし3次魔方陣を作る「規則性」は、市松模様の時のように規則性を見つけることができませんでした。これは3次魔方陣が特殊だからなのでしょうか?もう少し考察していけばわかるかもしれません。
また、
1次魔方陣・・・1通り
2次魔方陣・・・なし
3次魔方陣・・・1通り
ということもわかりました。$${n}$$次魔方陣は何通りあるのか調べていきます。最後まで読んでいただき、ありがとうございました!

