
数学美術館(連分数)
今回の記事は、数式を「見て」楽しんでいただきたいと思って記事を書きました。
数学が苦手な方でも楽しんでもらえるとうれしいです!!
今回取り上げるのは、「連分数」というものです。
小学校で分数を学習しました。
例えば、
$${\frac{1}{2}、\frac{3}{10}、\frac{51}{113}}$$・・・
数学では、分数の中に分数を入れた式「連分数」というものがあります。
実は連分数で表すと、とても美しいと感じる式がいくつかあるので紹介します!!
・ √2の連分数
中学校で学習した$${\sqrt{2}}$$。
その値を覚えさせられた方もいるのではないでしょうか。
$${\sqrt{2}=1.41421356・・・}$$
(ひとよひとよにひとみごろ・・・)
$${\sqrt{2}}$$は、数字がばらばらにずーと続くのですが、連分数で表すとこうなります。

普通だとばらばらなのに、連分数にすると規則性が見えます。
美しくないですか??
$${sqrt{3}}$$の連分数も紹介しておきます。
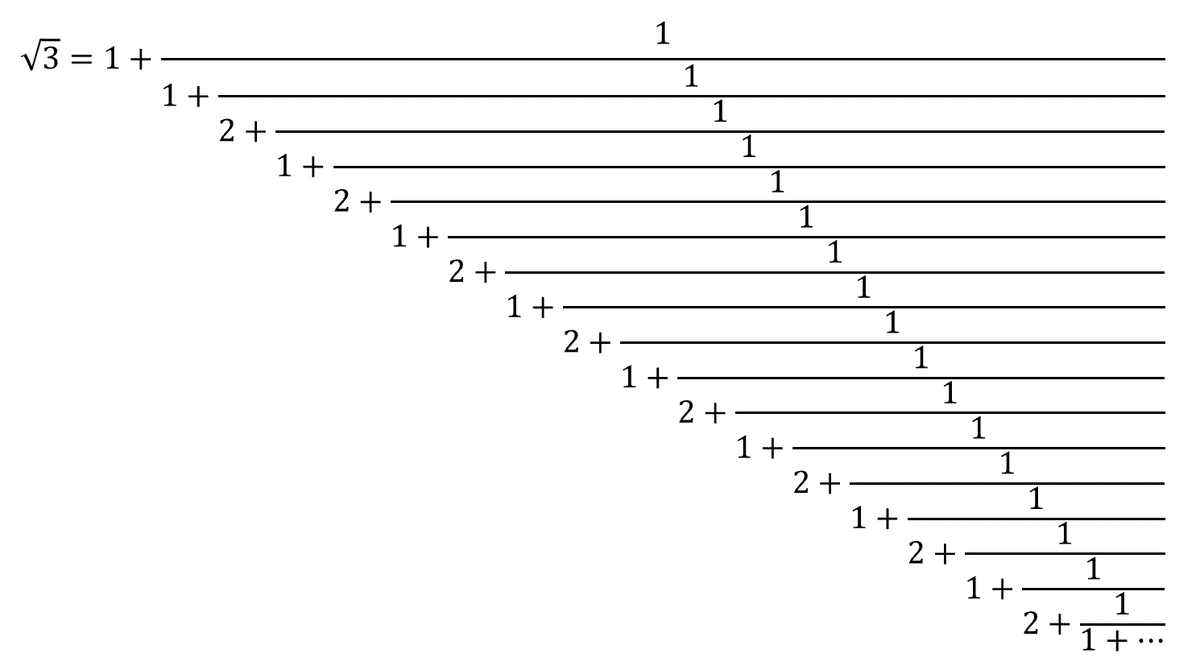
・ 黄金比の連分数
黄金比は、自然界や美術品など、様々なところに表れる比です。
具体的には、$${1:\frac{1+\sqrt{5}}{2}}$$を黄金比といいます。
この$${\frac{1+\sqrt{5}}{2}}$$を連分数で表現するとこうなります。

個人的には、これが最も美しいと感じます。
自然界の「美」を表すには、「1」だけでいいなんて・・・
・ 円周率πの連分数
円周率πは小学校からずーと使い続けますね。
実は、このπを連分数にしてもきれいではありません。
これはπが超越数という、ちょっと特殊な数だからです。
でも、こんなものならあります。

・ ネイピア数eの連分数
高校数学で微分積分まで学習した方なら、このネイピア数もご存じのはず。
ネイピア数も超越数です。

いかがでしたでしょうか?
連分数という、特殊な表現をすると、とてもきれいな数式になる場合があります。
ここでは、連分数について詳しく触れませんでしたが、興味のある方は勉強してみてください。
高校で学習するユークリッドの互除法を理解していれば、考え方はすぐ分かります。
最後まで読んでいただき、ありがとうございました!!

