
角の三等分は「絶対」できないの?
こんにちは。
今回の記事では、角の三等分線は絶対にかけないのか書いていきます。
最後まで読んでいただけると、うれしいです!
1 角の三等分線とは?
$${∠AOB}$$を三等分する直線を$${OC, OD}$$を、角の三等分線といいます。(図1)

実はこの角の三等分線の作図方法については、古代ギリシャ時代から考えられてきた問題で、19世紀にコンパスと定規では作図不可能なことが証明されました。
角の三等分線をかくには、コンパスと定規を使う+αが必要です。
その+αの部分が、折り紙または曲尺です。
2 折り紙で角の三等分線をかく
折り紙を使うと、角の三等分線をかくことができます。
実際に、角の三等分をやってみます。
今回は、角の大きさが60°の角を三等分します。

まず図2のように、下から同じ幅で2回折ります。幅は任意の長さです。

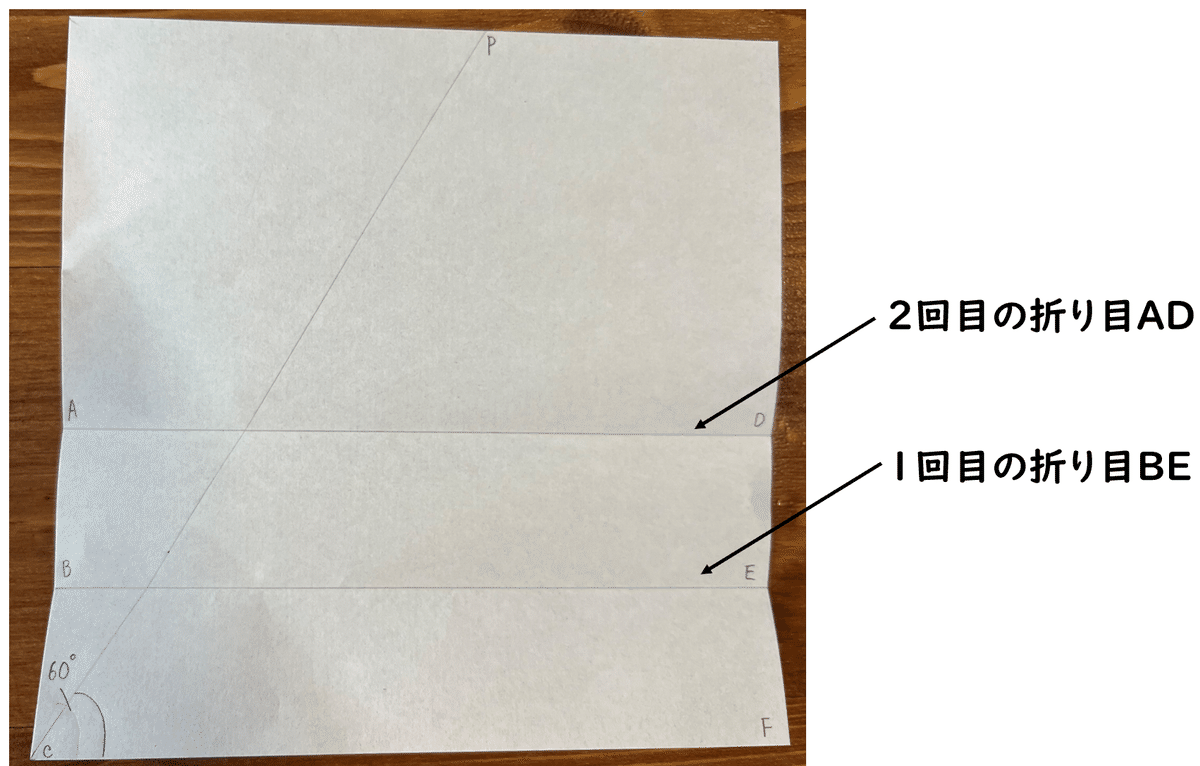
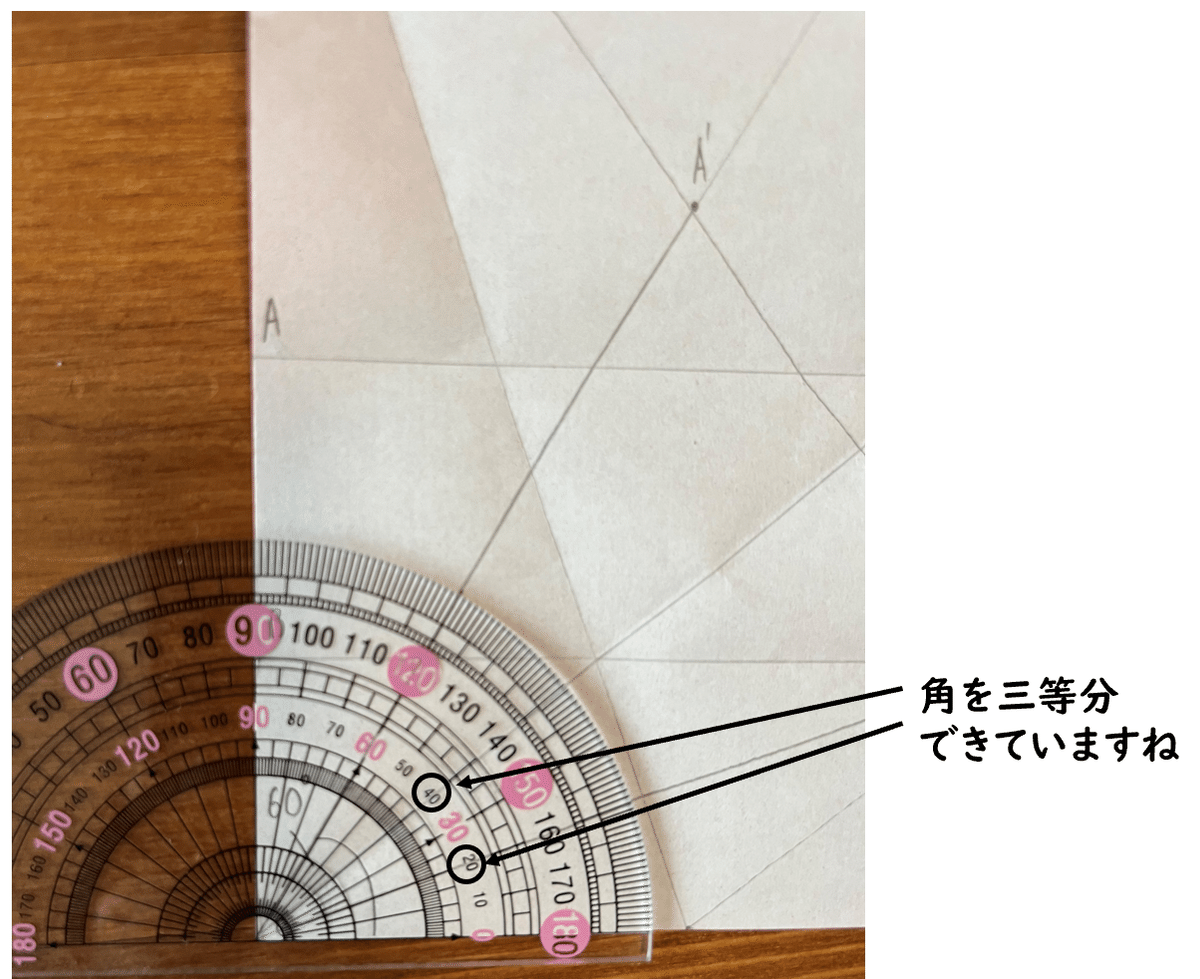
次に、図3の点Aが線分CP上に、点Cが線分BE上にくるように折ります。このとき、点Aが線分CP上にきた点をA'、点Cが線分BE上にきた点をC'とします。(図4)

最後に、線分A'C'を二等分するように折ります。(図5)


線分CC', CGが∠60°の三等分線です。

・ 証明
まず、線分BC'は線分ACを垂直に二等分しています。
このことから、△ABC'とCBC'は、2組の辺とその間の角がそれぞれ等しいので合同です。
合同な図形の性質より、
$${∠AC'B=∠CC'B}$$


次に、図11の赤い線は点Aが点A'に、点Cが点C'にくるように折った折り目です。
このとき、図11の緑と黄の三角形は、線対称だから合同です。
よって、
$${∠A'CC'は二等分されていることがわかります。

最後に、平行線の錯角は等しいから、
$${∠BC'C=∠C'CF}$$

これで、角の三等分線が作れることを示せました。
3 曲尺で角の三等分線をかく
折り紙でできても、現実的じゃない・・・
と思っちゃいますよね。
安心して下さい。曲尺でもできます。

では、折り紙の時と同じように、60°の角を三等分していきます。

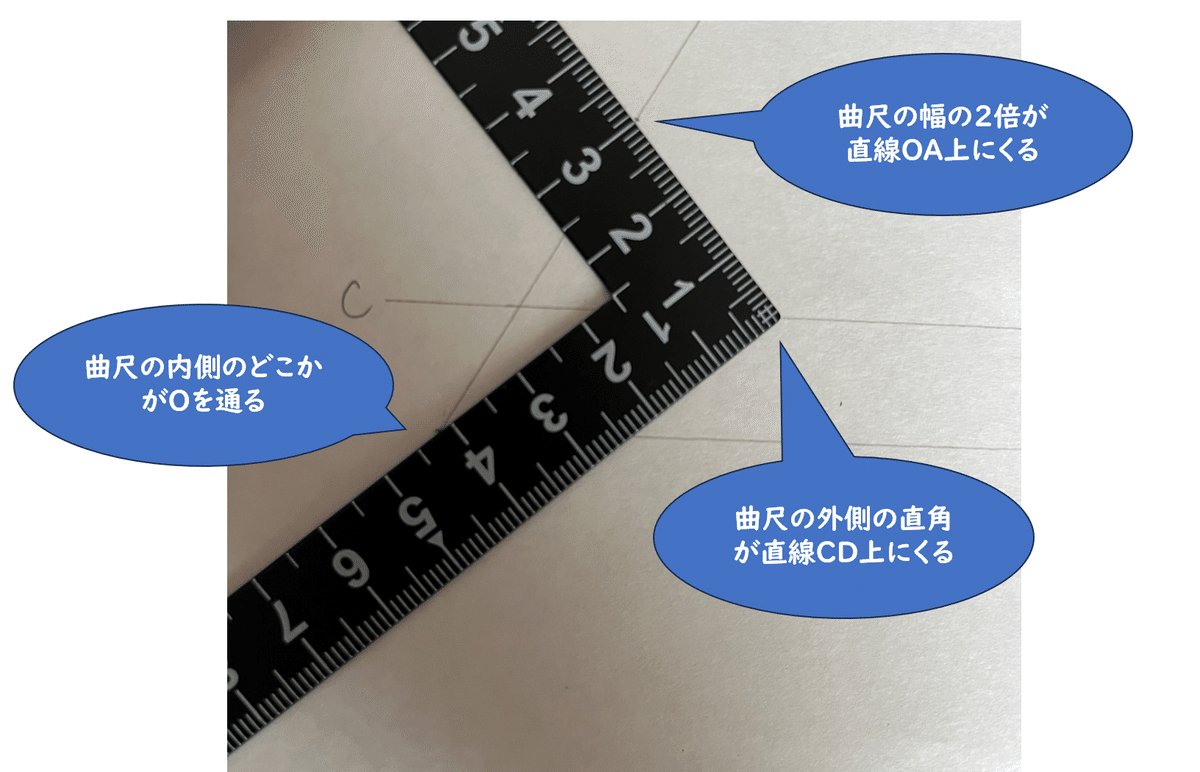
まず、OAと平行で、OAとの距離が曲尺の幅と同じ直線CDをOAの上側にかきます。(図15)

次に、曲尺の内側のどこかがOを通り、曲尺の外側の直角が直線CD上にきて、さらに曲尺の幅の2倍(この曲尺の幅は15mmだから、倍の30mm)が直線OA上にくるようにする。(図15)
このとき、CD上の点をP、OA上の点をQとします。

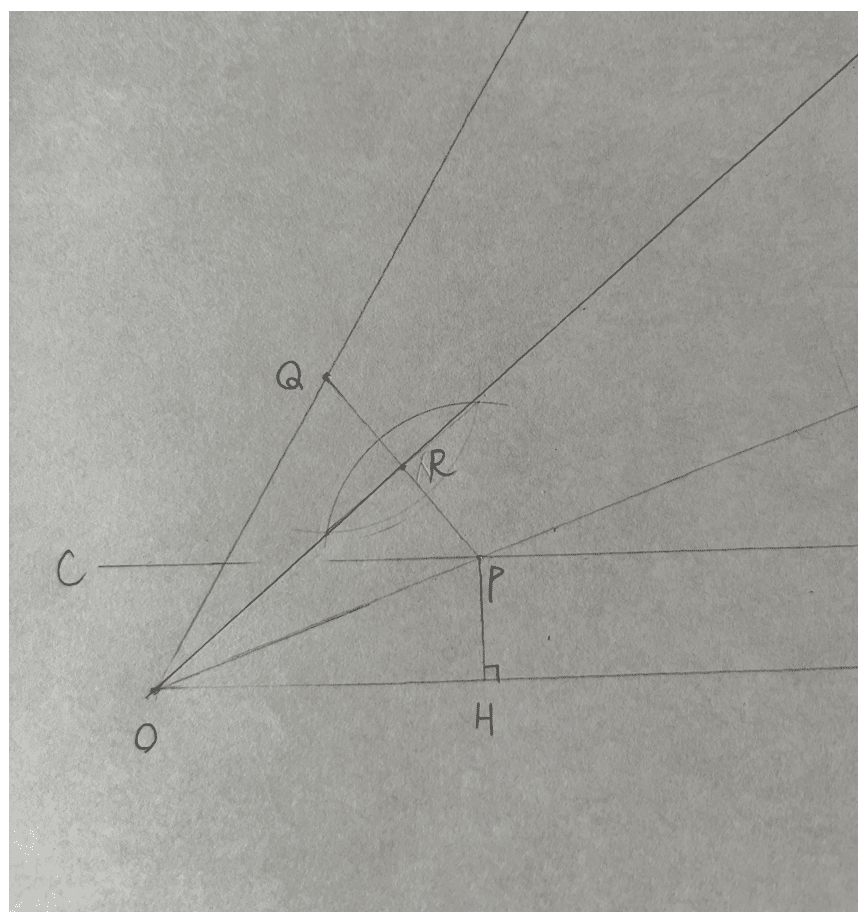
最後に、線分PQの中点Rを作図します。(垂直に等分線をかけばいいです)
半直線OP, ORが∠AOBの三等分線です。

・ 証明
点Pから半直線OAに垂線PHをおろします。
△OPRと△OQRで、
PR=QR
ORは共通
点P, Qの作図方法から
∠ORP=∠ORQ=90°
よって、
△OPR≡△OQR ①
次に、△OPRと△OPHで、
曲尺の幅は、もちろん等しいから
PR=QR
OPは共通
∠ORP=∠OHP=90°
よって、
△OPR≡△OPH ②
①、②より
△OPR≡△OQR≡△OPH
よって、
∠QOR=∠ROP=∠POH
証明終わり
4 おわりに
いかがでしたでしょうか。
このように、コンパスと定規だけではできなくても、他の道具を使えばできるというのはおもしろくないですか?
私は曲尺でできるというのを知った時、先人たちのモノづくりに対する熱意を感じました!!
最後まで読んでいただき、ありがとうございました!!

