
なぜ市松模様で魔方陣がつくれるの?〜数学好きの素人が証明してみた〜
1 はじめに
前回の記事で、市松模様を使えば次数が4や8の魔方陣を作れることを実際に示しました。
その記事の最後に、一般的に次数が$${4k}$$の魔方陣(以降、$${4k}$$次魔方陣という)は市松模様を使って作れるのか?という疑問を書きました。
なので、この記事では証明を考えたので、読んでいただければうれしいです。また、ずぶの素人の証明なので、穴があればコメントでやさし~~く教えていただけると、とても嬉しいです(笑)
2 証明する命題との方針
・ 市松移動
市松移動とは、魔方陣を作るために次のように数字を移動させることです。四次魔方陣を使って説明します。
まず、1~16の数を16のマスに配置します。次に図のように市松模様になるようにマスに色をつけます。

最後に緑に塗ったマス目の数だけ、中心に関して点対称移動させて魔方陣の完成です。

・ 証明する命題
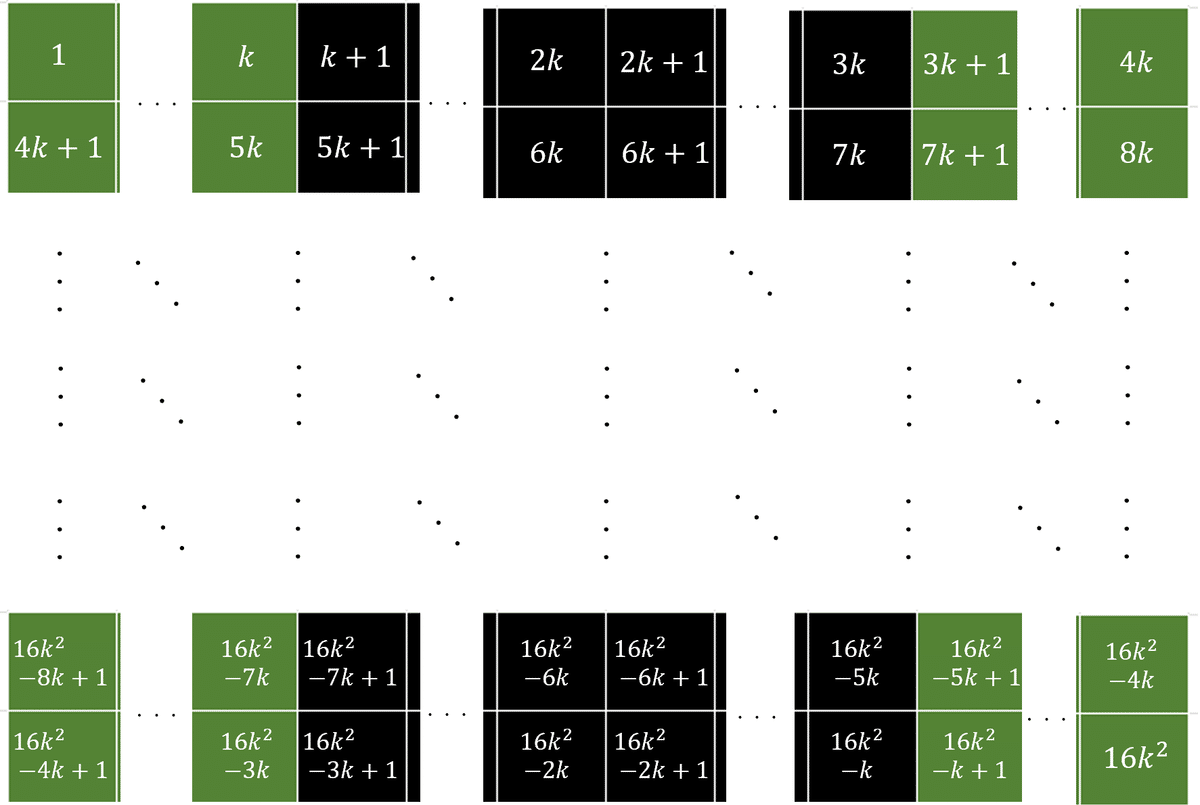
縦に$${4k}$$個、横に$${4k}$$個のマスを作り、そのマスに左上から右に向かって1、2、3、・・・、$${16k^2}$$と書いた表を作ります。
この表に、市松移動を適用すると、$${k}$$次魔方陣を作ることができる。
・ 証明の方針
$${4k}$$次魔方陣を作れた場合の斜めの数の和を求める。
$${a}$$を$${4k}$$以下の任意の自然数とします。上から$${a}$$行目と下から$${a}$$行目に市松移動を適用して、1で求めた和と等しいことを確認する。
3 4k次魔方陣の斜めの数の和を求める
まず4次魔方陣と8次魔方陣を、もう一度よく観察します。そしたら、市松移動をしても斜めの数は移動の対象にならないことがわかります。

このことを使えば、$${4k}$$次魔方陣の斜めの和を求めればよいとることができます。つまり$${1、4k+1、8k+2、12k+3、…、16k^2}$$の和を求めます。この数列は、初項1、公差$${4k+1}$$、項数$${4k}$$の等差数列です。
よって、$${4k}$$次魔方陣の斜めの和は、
$${2k(16k^2+1)}$$
です。
4 上からa行目と下からa行目に市松移動を適用して、3で求めた和と等しいことを確認する
・ 8次魔方陣で確かめる
8次魔方陣を作る前、つまり市松移動させる前の表の2行目に注目します。この行を4等分して、等分したマスに書いてある数の和を求めると、19,23、27、31です。また四等分したブロックを、左から順に第1ブロック、第2ブロック、第3ブロック、第4ブロックと呼ぶこととします。そして、第1ブロックと第4ブロック、第2ブロックと第3ブロックを足すとどちらも50になります。(下の図参照)

これはどの行でも第1ブロックと第4ブロック、第2ブロックと第3ブロックを足すと同じ値になります。理由は、各行に書いてある数の列が等差数列だからです。
市松移動する場合は、7行目の第2・3ブロック(または第1・4ブロック)が2行目に移動してきます。よって上から2行目の和は260です。
この値は、3で求めた式$${2k(16k^2+1)}$$に$${k=2}$$を代入した値と一致する。

・ 一般的に考える
$${4k}$$次魔方陣にする前の上から$${a}$$行目の行の左端の数は、$${4k(a-1)+1}$$です。上から$${a}$$行目の行にある数の和は、初項$${4k(a-1)+1}$$、公差1、項数$${4k}$$の等差数列の和を求めればいいです。
$${\displaystyle\sum_{l=1}^{4k} {4k(a-1)+l}}$$
$${=4k×4k(a-1)+2k(4k+1)}$$
$${=16k^2(a-1)+2k(4k+1)}$$
市松移動で第2、3ブロックを移動させる、つまり残るのは第1、4ブロックの和で、それは上で求めた和の半分の数だから
$${{16k^2(a-1)+2k(4k+1)}÷2}$$
$${=8k^2(a-1)+k(4k+1)}$$ (ア)

次に移動させた第2、3ブロックの位置に移動してくるのは、下から$${a}$$行目の第2、3ブロックで、その和が上から$${a}$$行目の行に加えられます。
では、下から$${a}$$行目の行にある行の第2、3ブロックの和を求めます。
下から$${a}$$行目の行にある行の一番右にある数は、$${16k^2-4k(a-1)}$$です。この行の和は、
$${\displaystyle\sum_{m=0}^{4k-1} {16k^2-4k(a-1)-m}}$$
$${=16k^2×4k-4k×4k(a-1)-2k(4k-1)}$$
$${=16k^2(4k-a+1)-2k(4k-1)}$$
第2、3ブロックの和はその半分だから、
$${{16k^2(4k-a+1)-2k(4k-1)}÷2}$$
$${=8k^2(4k-a+1)-k(4k-1)}$$ (イ)

市松移動したときの上から$${a}$$行目の和は、(ア)と(イ)の和だから、
$${8k^2(a-1)+k(4k+1)}$$
$${+8k^2(4k-a+1)-k(4k-1)}$$
$${=32k^3+2k}$$
$${=2k(16k^2+1)}$$
これは、3で求めた斜めの和と等しいです。
これで、市松移動をすると、必ず和が$${2k(16k^2+1)}$$の行を作れるといえます。
また、列に関しても同じで、魔方陣を作る前の縦に並んだ数は等差数列だから、市松移動をすると、必ず魔方陣が作れることがいえます。
5 おわりに
この証明を考えるのに1日以上かかっちゃいました(笑)
また今回は、魔方陣の斜めの数は市松移動しても変わらない場合を考えましたが、前回の記事でも書いたよう市松模様でなくても、次の条件を満たす模様ならば魔方陣を作ることができる模様があります。
上下左右に対称で、各行各列のマス目の半分が緑に塗られていること。
この条件を満たすのならばなぜ作れるのか、気になりました。
今回の証明は、高校数学の数列の知識があれば解けると思うので、もしこの記事を読んでいただいている高校の先生がいらっしゃいましたら、生徒に出してみていただけるとうれしいです!そのときはコメントで感想をいただけると、励みになります!
最後まで読んでいただいて、ありがとうございます!

