
数学美術館(素数)
今回は私が愛して止まない素数について紹介します!!
この記事を楽しんでもらうために、最初に基礎知識だけお伝えします。
その後は、素数の不思議について紹介します。
基礎知識
素数とは、1とそれ自身以外の数で割り切れない数。
具体的には、2,3,5,7,11,13などである。
素数は無限に存在する
素数が無限にあることは、ユークリッドが「原論」で2000年前にすでに証明しています。
凄いですね!!
以下は、ユークリッドの証明を書きます。
興味のある方のみお読みください。
(証明)
素数が有限であると仮定します。
すべての素数を$${p_1,p_2,…p_n}$$とします。
このとき、自然数$${q}$$を
$${q=p_1p_2…p_n+1}$$
とします。
$${q}$$は、$${p_1}$$でも、$${p_2}$$でも、$${p_3}$$でも割り切れません。
どの$${p_i}$$でも割り切れないので、$${q}$$は合成数ではありません。
しかし、$${q}$$を素数とすると、どの素数$${p_i}$$とも異なるので仮定に反します。
よって、矛盾である。
この矛盾は最初の仮定「素数が有限である」が間違っています。
よって、素数は無限に存在します。
・素数のいる場所(Excel編)
1から100の中にある素数に色をつけてみました。
どうでしょうか?
3,5,7のように1つ飛びで現れることもあれば、89の次の素数は97のように7つ飛びの場合もあります。

つまり、出てくるのはバラバラなんです。

ExcelとCHAT GPTを使って作成しました。
左上が1で、右下が100000です。
この模様に規則性を見つけたら、大発見です。
・素数のいる場所(チェビシェフ編)
上で書いたように、素数の出現する頻度はバラバラ。
でも、どこにあるかはある程度分かる。

具体的には、$${n=1000000}$$のとき
1000000から2000000の間に、必ず素数があると言えるのです。
「ん?そんなに大きな区間なら、素数があるのは当たり前だろ!!」と思うかもしれませんが、絶対あるかどうかは調べないと分かりません。
ですが、これは調べなくても絶対あると言い切っているのです。
ちなみに、素数が出てこない、とても大きな区間を作ることは可能です。
例えば、ある素数の次の素数は1兆個先、みたいなパターンです。
なので、このチェビシェフの定理は、すごいことなんです。
・素数のいる場所(ガウス編)
次に、数学の超天才であるガウスが予想し、その百年後に証明された定理です。
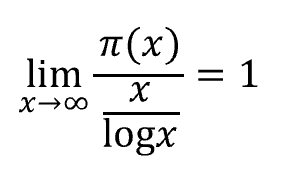
これ、何を表現しているかというと、ある値までの素数の個数がおおよそわかるという定理です。
この「ある値」が大きければ大きいほど、誤差が少なくなります。
例えば、$${10^{28}}$$までに含まれる素数の個数を、概算することができます。
重要なのは、実際に調べなくてもおおよそ分かるということです。
・双子素数
次は、数学界の双子の紹介です。
素数の中で、
3と5
5と7
17と19
のように、引き続いた2つの奇数がともに素数のとき、それらを双子素数といいます。
今分かっている最大の双子素数を紹介します。
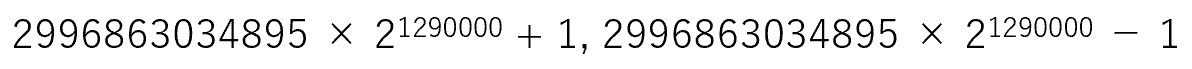
この2つの数は、388342桁もある巨大な数です。
ちなみに、双子素数が無限に存在するかは不明です。
あと、三つ子素数だってあります。
面白いですね!!
・ソフィ・ジェルマン素数
素数$${p}$$があり、$${2p+1}$$も素数になるとき、$${p}$$をソフィ・ジェルマン素数といいます。
例えば、2,3,5,11などがソフィ・ジェルマン素数です。
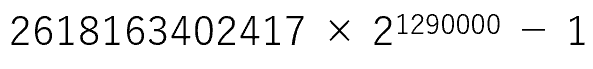
これは、388342桁もある巨大数です。
ソフィ・ジェルマンとは、1700年代から1800年代にかけて活躍した女性数学者の名前です。
この方が生きた時代は、女性が学問を学ぶことが否定的だったため、男性のふりをしてガウスと文通していたようです。
また、この方は、有名なフェルマーの最終定理の解決にとても貢献しました。
おわりに
素数の美術館、いかがでしたでしょうか?
不規則な中に、先人たちが規則を見つけようとした様子が見られたでしょうか?
また、特別な素数についても紹介しました。
このような特別な素数は、こちらの記事でも紹介しているので、ぜひご覧ください!!
もし興味が湧きましたら、整数論という数学の分野を覗いてみてください!
最後まで読んでいただき、ありがとうございました!!

この記事が気に入ったらサポートをしてみませんか?
