人はどんなときに有能な学び手になるのだろうか？
前回までの３つの記事で、これまでの伝統的な学習観を（現行の学習指導要領で獲得させる資質・能力「学びに向かう力」とも絡めて）否定して新しい学習観を創造する必要性や、学び手がどのようなときに能動的な学ぶかについて書いてきました。
前回までの３つの記事は、この記事の最後に掲載しましたので、もしご興味がありましたら、読んでいただけるとうれしいです。
今回の記事では、新しい学習観の「学び手は有能である」というところに焦点を当てています。
１ 学び手が有能であるのはどのようなときか
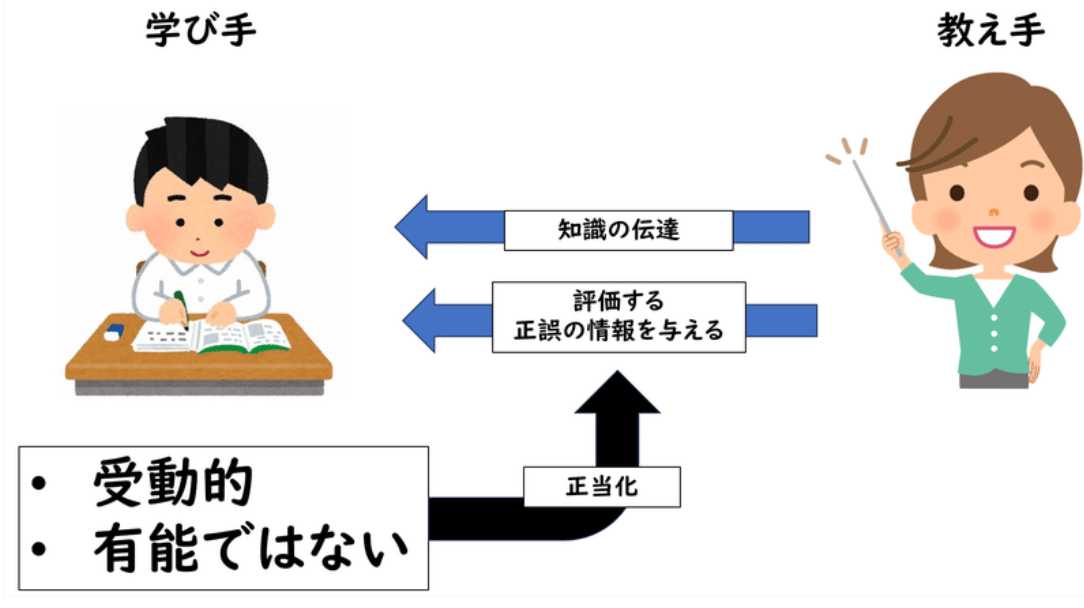
まず、新しい学習観において「学び手は、能動的で有能である」という仮定しました。
ここで気をつけたいのは、能動的だから有能であるわけではないということです。
では、どのようなときに学び手は有能なのでしょうか。
それは、言語や数の獲得における学習のときです。
２ 言語や数の獲得における学習
これは赤ちゃんや幼児をイメージしてもらうと分かりやすいです。
赤ちゃんや幼児は、大人から明確な理論を学んで言語や数を獲得するでしょうか？
・ 言語の獲得において
言語を獲得するというのは、正しい文を作る力を獲得するということです。
正しい文を作るには、
語彙の理解と正しい文法を理解する必要があります。
では、赤ちゃんや幼児が日常生活で耳にする文には、正しい文法を作るための情報が明示的に与えられるでしょうか？
与えられませんね。
文法における品詞の区別や句、節についても明示されません。
また、幼児が文法的に適格でない文を言っても、親は訂正しないことが多いです。
文法のような規則の獲得においては、正しい事例と正しくない事例から、帰納的な推論を通して、規則を獲得します。
ですが、文法の獲得ではこのような推論が起こらない。
でも、文法を理解することができる。
これは、人間が生まれながらにもっている認知的制約のおかげです。
認知的制約とは、次の意味です。
認知的課題を遂行する際に、検討するべき仮説や探索すべき情報があらかじめ制限されている状態を指します。
新生児や幼児が短い時間で学習を進める際に、この制約が重要な役割を果たすと言われています。
例えば、図６のようなに、大人が「半分だね」といったときに、既有知識から「半分」というのが何を指すのか、仮説の範囲を縮小させられます。
・ 数の獲得において
ゲルマン（※）によって、計数（事物を数える）を適切に行う５つの原理が示されました。
事物とラベル（１，２，３、・・・という符号）が１対１で対応する原理
ラベルはいつも同じ順序で配列される（順序の原理）
数え上げたときに最後に用いられたラベルが、その集合の大きさを表す（基数の原理）
計数の手続きは、どんな集合にも適応できる（抽象性の原理）
集合中のどの要素から数えてもよい（順序無関係の原理）
この５つの原理を、完全ではないが人は生得的に獲得しているため、より進んだ数の理解が可能になる。
３ 結論
このように、人は初期の言語や数の獲得においては生得的な認知的制約によって、有能であるといえる。
私も１歳半になるこどもがいるが、順序の原理や抽象性の原理が見られる場面があります。
人間はすごいな～と実感します。
最後まで読んでいただき、ありがとうございました！
・ 参考文献
人はいかに学ぶか 日常的認知の世界 稲垣佳代子 波多野誼余夫 著 中公文庫
※ 数に関する基本的諸能力 ゲルマン 1983
・ 前回までの３つの記事
この記事が気に入ったらサポートをしてみませんか？