無限に足すと、無限に大きくなるの??(後編)
1 はじめに
前回の記事「無限に足すと、無限に大きくなるの??(前編)」では、以下の問題を解くための数列の無限和について基礎知識を紹介しました。
【問題】
面積が1の正三角形があります。この正三角形に次の操作を、次々にしていきます。
(操作)
操作する前の正三角形の各辺の三等分点を頂点にもつ正三角形を、操作する前の正三角形の外側に付け加える。

操作を続けていくと、図形の面積はどうなると思いますか?
では、後編ではこの問題を解いていきます。最後に、この問題に関する数学の一分野を紹介します。
最後まで読んでいただけるとうれしいです。
2 問題の図形の面積は無限に大きくなるタイプだろうか?
・ 数列の無限和は、2つのパターンがある
(パターン1 ある値に収束する)
これは前回紹介した数列の無限和:
$${\frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+…=1}$$
がこのパターンです。この無限和は1に収束します。
(パターン2 無限大に発散する)
$${1+2+4+8+16+…}$$という無限和は、収束せず無限大に発散します。
・ 2つのパターンの違いはなんだろうか?
もう一度、2つの数列の無限和を並べてみて考察します。
$${\frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+…=1}$$・・・①
$${1+2+4+8+16+…=∞}$$・・・②
違いは何かというと、①の数列は足す数が$${\frac{1}{2}}$$倍ずつされているのに対して、②は2倍ずつされている部分です。
このように、足す数が$${r}$$倍ずつされている数列の無限和を、無限等比級数といいます。そして、この$${r}$$の絶対値が1未満になるような無限等比級数は収束して、1以上だと無限和は無限大に発散します。
・ 2つの無限和をグラフにして収束するか見てみる
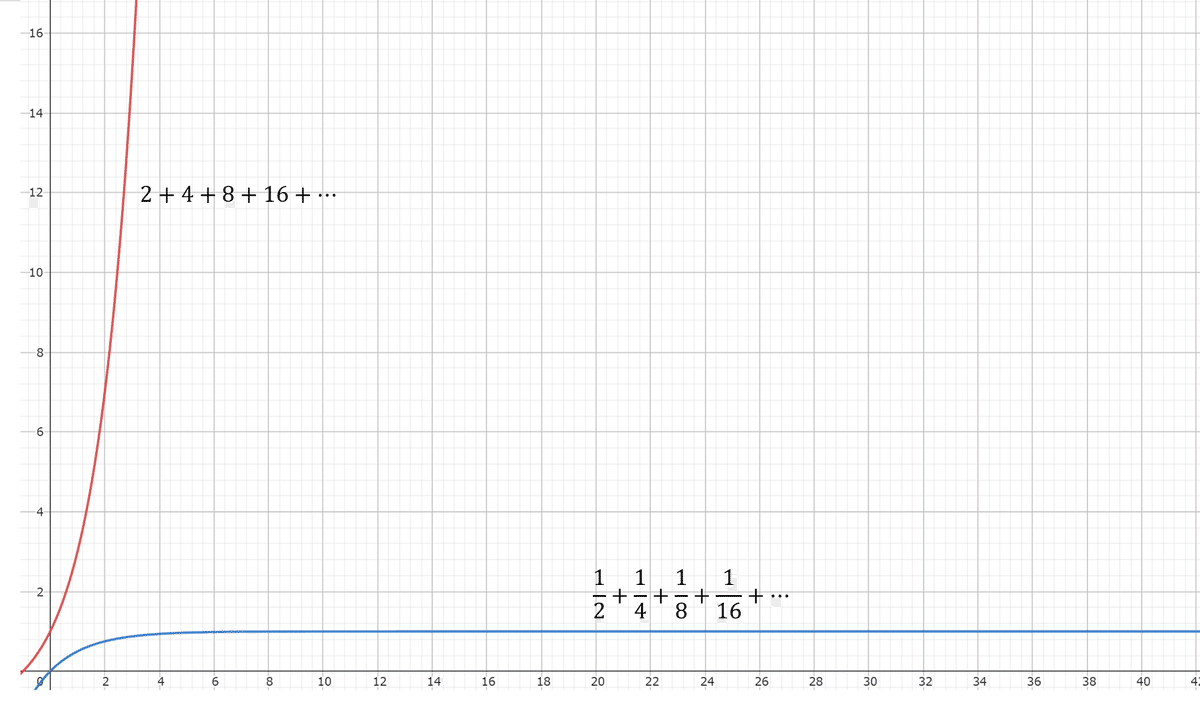
このグラフを見ると、どちらがある値に収束するかは一目瞭然ですね。
・ 図形の面積を求める途中式を書いてみる
操作する前の面積1の正三角形の一辺の長さを$${a}$$とします。
操作を1回したときの面積を求める途中式をかきます。操作1回の図を下に示します。また、元の三角形の外側につけた正三角形に注目します。

赤い正三角形の面積は、
$${\frac{1}{2}×\frac{1}{3} a×\frac{1}{3}a×\sin 60°=(\frac{1}{3})^2×\frac{1}{2}a^2\sin 60°}$$
ここで、$${\frac{1}{2}a^2\sin 60°=1}$$だから、(操作する前の正三角形の面積は1なので)
$${(\frac{1}{3})^2×\frac{1}{2}a^2\sin 60°=(\frac{1}{3})^2×1=(\frac{1}{3})^2}$$
赤い正三角形は3つあるので、操作1回したときの図形の面積は、
$${1+(\frac{1}{3})^2×3=1+\frac{1}{3}=\frac{4}{3}}$$
まだ規則性が見えないので、操作を2回したときの図形の面積も同様に求めます。

この図形の面積は、操作を1回したときの図形に新たに外側に付け加えた正三角形の面積を足せばいいので、
$${\frac{4}{3}+\frac{1}{2}×(\frac{1}{9}a)^2×\sin 60°×12=\frac{4}{3}+(\frac{1}{9})^2×12}$$
これを計算すると、$${\frac{40}{27}}$$です。
・ n回操作した図形の面積と(n+1)回操作したときの図形の面積の関係は?
$${n}$$回操作したときの図形の面積を$${S_n}$$、$${n+1}$$回操作したときの図形の面積を$${S_{n+1}}$$、$${S_n}$$に付け加えた正三角形の面積の合計を$${x}$$とすると、上の途中式から、$${S_{n+1}=S_n+x}$$といえます。
$${x}$$について考えます。
$${S_n}$$に付け加える正三角形の数は、$${S_n}$$の辺の数と等しいです。操作をすると辺が1本から4本に増えることは図から分かります。
$${n}$$回操作したときの図形の辺の数は、$${3×4^n}$$です。

次に増えた三角形1つの面積です。辺の長さが分かればよいので、1辺を3等分していることから、$${n}$$回操作したときの辺の長さは$${(\frac{1}{3})^na}$$です。$${n+1}$$回操作すると、$${n}$$回操作したときの辺の長さが$${\frac{1}{3}}$$されます。
これらを踏まえて、
$${x=\frac{1}{2}×((\frac{1}{3})^na×\frac{1}{3})^2×\sin 60°×3×4^n}$$
$${=(\frac{1}{9})^n×\frac{1}{3}×4^n}$$
$${=\frac{1}{3}(\frac{4}{9})^n}$$
$${S_{n+1}=S_n+\frac{1}{3}(\frac{4}{9})^n}$$だから、
$${S_n=S_{n-1}+\frac{1}{3}(\frac{4}{9})^n+\frac{1}{3}(\frac{4}{9})^{n-1}}$$
$${=S_{n-2}+\frac{1}{3}(\frac{4}{9})^n+\frac{1}{3}(\frac{4}{9})^{n-1}+\frac{1}{3}(\frac{4}{9})^{n-2}}$$
$${=……}$$
$${=S_0+\frac{1}{3}(\frac{4}{9})^n+\frac{1}{3}(\frac{4}{9})^{n-1}+\frac{1}{3}(\frac{4}{9})^{n-2}…+(\frac{4}{9})^0}$$
$${S_0}$$は操作前の正三角形の面積だから1なので、
$${S_n=1+\frac{1}{3}(1+\frac{4}{9}+(\frac{4}{9})^2+…+(\frac{4}{9})^n)}$$
・ nを限りなく大きくすると・・・
$${S_n=1+\frac{1}{3}(1+\frac{4}{9}+(\frac{4}{9})^2+…+(\frac{4}{9})^n}$$で、$${n \to ∞}$$を考えます。
$${1+\frac{4}{9}+(\frac{4}{9})^2+…+(\frac{4}{9})^n}$$の等比級数は、
$${T=1+\frac{4}{9}+(\frac{4}{9})^2+…+(\frac{4}{9})^n)}$$・・・①
両辺$${\frac{4}{9}}$$をかけると、
$${\frac{4}{9}T=\frac{4}{9}+(\frac{4}{9})^2+(\frac{4}{9})^3+…+(\frac{4}{9})^{n+1}}$$・・・②
①ー②
$${\frac{5}{9}T=1-(\frac{4}{9})^{n+1}}$$
$${T=\frac{9}{5}-\frac{9}{5}(\frac{4}{9})^{n+1}}$$
つまり、
$${S_n=1+\frac{1}{3}(\frac{9}{5}-\frac{9}{5}(\frac{4}{9})^{n+1})}$$
$${=1+\frac{3}{5}-\frac{3}{5}(\frac{4}{9})^{n+1}}$$
$${=\frac{8}{5}-\frac{3}{5}(\frac{4}{9})^{n+1}}$$
$${n \to ∞}$$にすると、$${(\frac{4}{9})^{n+1} \to 0}$$だから、
$${S_∞ \to \frac{8}{5}}$$
つまり、操作を続けていくと、面積は$${\frac{8}{5}}$$
3 次々に三等分して出来上がるフラクタル図形
長さが1の線分に対して、次のような操作をします。
線分を三等分して、真ん中の線分を底辺とする正三角形を描くように線分を飛び出させる。
できた線分に対して、1と同じ作図をする。

このように操作をしていくと、「コッホ曲線」という有名な図形が現れます。複雑な図形ですが、全体の一部分を拡大すると同じようなくり返しのパターンが現れます。これを「自己相似性」といい、このパターンを「フラクタル」といいます。フラクタルは、入道雲やカリフラワー、枝分かれした木などなど身近なものにも見られます。
このような複雑な図形を扱う数学の分野の「フラクタル」は、同じく複雑な現象を取り扱う「カオス理論」と合わせて、これまで解析できないとされてきたことの理解をするために武器になるかもしれないと期待されています。
4 おわりに
最初に示した問題から、無限等比級数の収束や数学の1つの分野「フラクタル」について説明しました。最初に示した問題は、香川大学の入試問題として出題された問題です。「フラクタル」は大学で学習する内容ですが、その入り口のような問題は大学入試で出題されることがあります。大学入試問題を入り口に、大学で学習する分野をかいつまんでみるのも面白いですね。
またこの記事で、無限に数を足していっても、無限大に大きくなるわけではないということを知っていただけたら嬉しいです。
最後まで読んでいただき、ありがとうございました!!

