
部分分数分解の公式の納得できなかったところ
こんにちは。
久々の記事になります。
最近仕事と数検1級に向けた勉強に時間を全振りしていて、記事を書く時間を捻出できませんでした。
これはいかん!!
ということで、久々に記事を書きます。
内容は、数学の「部分分数分解」というやつです。
数検1級に向けた勉強をしていて、なぜ?と感じたところだったので自分なりにまとめました。
もし、高校生で同じ疑問を持っている方がいらっしゃれば、一助になると幸いです。
1 部分分数分解とは?
部分分数分解について、簡単に説明します。
なんだか早口言葉にありそうな単語ですね笑
部分分数分解とは、ある分数の式を2つ以上の分数の式に分解することです。
言葉だけだと分かりにくいので、具体例を示します。
例
$${\frac{1}{x^2-1}}$$を部分分数分解すると、
$${\frac{1}{x^2-1}=\frac{1}{2}(\frac{1}{x-1}-\frac{1}{x+1})}$$
左辺は1つの分数の式だったものが、2つの分数の式に分解できました。
2 なぜ部分分数分解をするの?
なぜこんなことをするのか?と思いますよね。
実は部分分数分解することで、積分ができるようになるからなんです。
分数関数の積分に関しては、本題とずれてしまうので、この記事では取り上げません。
もしご興味ある方は参考書で確認いただければと思います。
3 分母の次数と分子の次数の関係
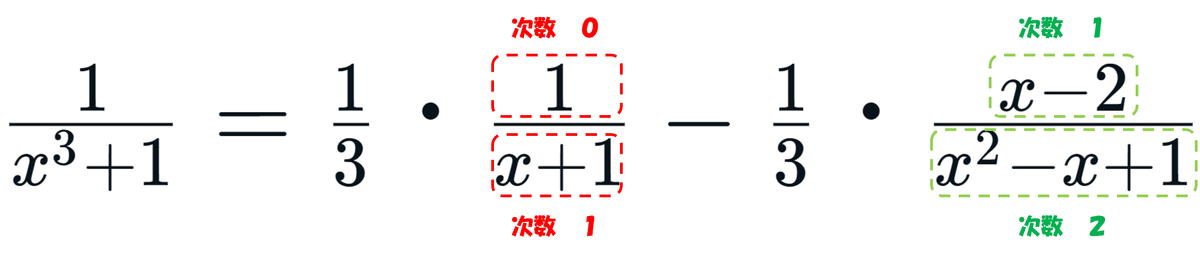
部分分数分解したとき、一般的には分母の次数より分子の次数が1だけ小さくなるように部分分数分解します。
具体的には、下の例の通りです。
4 納得できない公式
数検1級の参考書の問題と、公式を示します。
問題 次の式を部分分数分解しなさい。
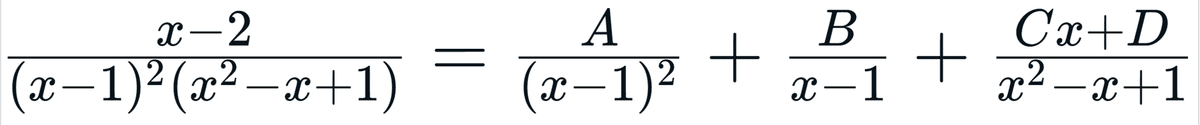
この公式で納得できないところは、下の図1の赤で示した部分です。

一般的には、分子の次数は分母の次数より1だけ小さくなるように部分分数分解しますが、図の赤で示した部分は次数が2小さいです。
これが公式で示されていますが、納得できませんでした。
5 公式を納得できるようにする
では上の図の公式の納得できないところを解決します。
まず一般的な形、つまり分母の次数が分子の次数より1だけ小さい形に部分分数分解したと考えます。(図2)

図2の右辺の第1項に注目して、次のような式変形をします。(図3)

図3の最後の行の第2項を見てください。
分母は$${(x-1)^2}$$で次数は2、分子は$${A+B}$$で次数は0。(図4)

よって、公式のような形に変形できると分かります。
公式を導きます。

図5の最後の式のA+B、A+Cを改めてそれぞれA , Bとする。
またDをC、EをDにする。

6 一般的に・・・
今回は、分母が$${(x-1)^2}$$でした。
では、$${(x-1)^2}$$が$${(x-1)^3}$$だったら、その部分分数分解したときの分子の次数はどうなるでしょうか。

もし部分分数分解すると、次のような形のはずです。(図6)

右辺の第一項に注目して、次のような変形をします。

図7の最後の式の分子の次数は、すべて0です。
この結果から予想できるのは、分母に$${(x+a)^n}$$($${a}$$は任意の実数)が含まれる式を部分分数分解をすると、分子の次数は必ず0だということです。
7 最後に
今回は数学検定1級の勉強をする中で疑問に感じたところを解決できました。
細かいところですが、1つ1つ納得しながら進むというのも大事だと思います。
最後まで読んでいただき、ありがとうございました!!

