
折り紙の数学入門(の入門)
こんにちは。
最近noteで数学の記事を書いていて、数学の面白さをずーっと毎日体感しています。
最近は計算するよりも、作図したり作ったりして数学を楽しんでいます。
今回は、折り紙についての数学を紹介します。
折り紙って小学校の頃にはよくしましたが、中学生以降あまりしませんでした。
でも「数学」という視点で見ると、面白いことがあると分かりました!
それを少しでもこの記事でお伝えできればと思います。
1 なぜ折り紙に興味をもったの?
折り紙に興味をもったのは、我が家のマイバッグを見てからです。
下の写真は、我が家のマイバッグ。(図1)

使わないときは小さく、使うときは結構な容量のあるバッグになります。
私は最初に妻がこれを開いて使っているのを見たとき、「すごい!」と興奮したのを覚えています。(妻はキョトンとしていましたが💦)
なぜ大きなマイバッグをこれほど小さく折りたたむことができるのか興味をもっていたのですが、最近折り紙についての本を何冊か読んで解決できました。
身近にある物に隠れた折り紙の数学について、紹介したいと思い、筆をとった次第です。(パソコンなので、筆ではなくキーボードですが)
2 折り紙とは
折り紙は、古くは平安時代まで遡るともいわれています。
日本人であれば、一度くらい鶴を折ることに挑戦した経験があるのではないでしょうか。
それほど日本人にとって、折り紙はとても身近な遊びです。
近年では、折り紙を遊びではなく、科学に応用するという動きが活発です。
太陽光パネルの「ミウラ折り」、軽量で高剛性の航空宇宙材料を作成するための「ハニカムコア」、製薬分野では細長い構造をもったタンパク質をどのように折りたたむかを研究する「タンパク質の折り問題」などです。
この記事では、折り紙の平坦折について考えていきます。
それが図1の「マイバッグを折りたためるか」の解決につながります。
3 マイバッグの折り目を観察
では、まずマイバッグを折りたたむときに必要な折り目を観察します。
折り方には、山折りと谷折りがあるので、赤線と青線で分けてます。(図2)
ここで念頭に置いておかないといけないのは、反対側からマイバッグを見た場合は、山折りと谷折りが入れ替わるということです。

この折り目を見てみると、折り目が集まってくる頂点が6個あって、そのどれもが山折りが1個、谷折りが3個集まってきています。(反対側から見ると、山折りが3個、谷折りが1個集まってくる)(図3)

上述しましたが、山折りと谷折りは見る面を反対にすると入れ替わるので、こういうことがいえそうだと予想できます。

では、これについての定理があるので、紹介します。
4 前川=ジュスタン定理
定理の主張は、このようになります。
平坦に折られた紙で、$${M}$$個の山折りと$${V}$$個の谷折りが1つの頂点でぶつかっているとする。
このとき$${M}$$と$${V}$$の差は2である。
ここで、平坦に折られた紙とは、折りたためられた紙と翻訳しても問題ないです。
ではなぜこれが成り立つのか、折り紙を折って説明します。
左は平坦に折った紙で、右はそれを展開したものです。
展開した紙の赤い線は山折りで、黒い線は谷折りです。
右の図の中心にある点Oに集まる山折りと谷折りの数の差は、たしかに2ですね。

では、なぜ前川=ジュスタン定理が成り立つのか、直感的に説明します。
ちゃんとした証明は、次の章で行います。
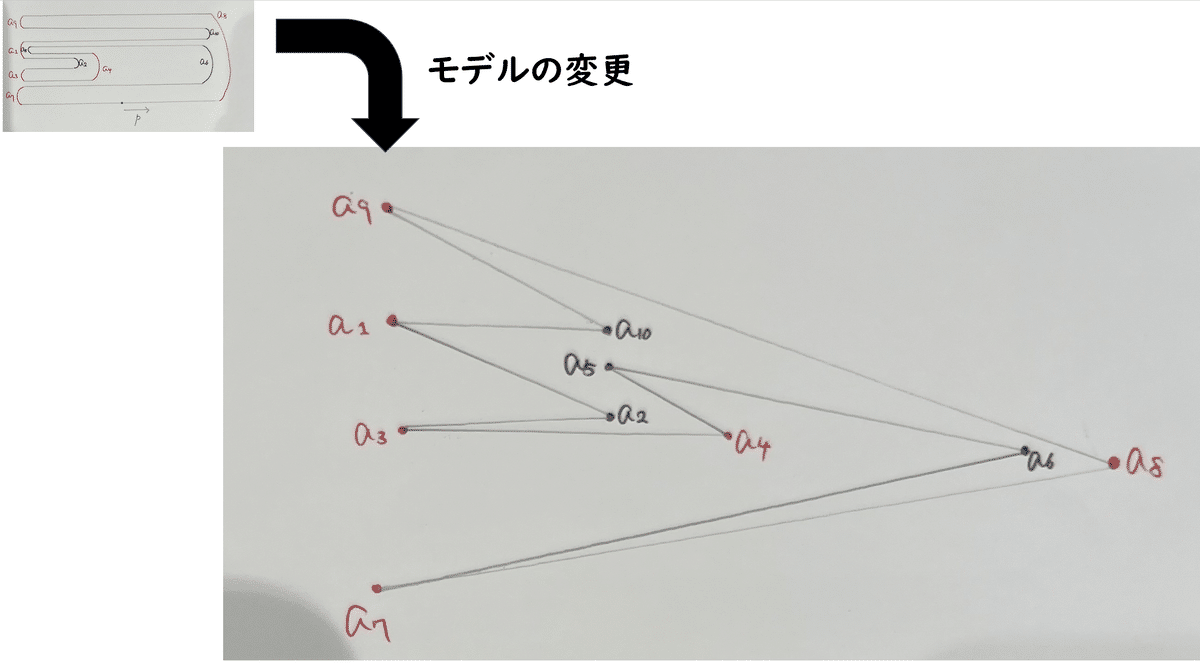
まず、図5のように、折り線と外枠の正方形との交点にラベルをつけます。
この状態で平坦に折ると、そのラベルが同じ側に集まります。

ラベルが集まった様子のモデルをかきます。

モデルに書いた点pを見てください。
この点pは右向きに進みます。
点pは最終的にスタート位置に戻ってくるのがわかります。
戻ってくれることができれば、平坦に折れると考えます。
点pが赤い線(山折り)に到達すると、向きが変わります。
同様に、黒い線に到達すると向きが変わります。
ここで、向きが変わるのを「回転」とみなせば、赤い線は180°回転、黒い線は-180°回転と考えられます。
では、点Pがスタート位置をスタートして、戻ってくるまでの過程と回転角をまとめます。

図7を見たらわかるように、赤い線(赤い文字)を6回、黒い線(黒い文字)を4回通るから、
$${180°×6-180°×4=360°}$$
です。
計算結果の「360°」とは、スタートして1回転して戻ってきていることを表しています。
前川=ジュスタンの定理は、平坦に折られた紙の山折りと谷折りの個数の差が必ず2でしたね?
つまり、差が2になれば図7に示した点pが必ずスタート位置に360°回転して戻ってこれるからなんですね。
5 前川=ジュスタン定理の証明
この定理の証明は、$${n}$$角形の内角の和は、
$${180°×(n-2)}$$
ということを使います。
このことの証明は、山根あきらさんのこちらの記事でわかりやすく解説されていますので、参考にされてください。
さて、さきほどの図6のモデルを、このように尖ったモデルに変えても本質は変わりません。
この証明では、この尖ったモデルを使います。
このモデルを完全に平坦になるまで押しつぶします。
そうすると、すべての山折りの頂点の内角は0°にきわめて近づき、すべての谷折りの頂点の内角は360°に近づけたと考えます。
山折りの個数を$${M}$$個、谷折りの個数を$${V}$$個とすると、完全に平坦になるまで押しつぶした内角の総和は、
$${M×0°+V×360°}$$
です。
この値は$${n}$$角形の内角の和と等しくなるから、
$${M×0°+V×360°=180°×(n-2)}$$
$${V×360°=180°×(n-2)}$$ ・・・①
$${n}$$角形の頂点の数は、$${M}$$と$${V}$$を使って、
$${n=M+V}$$
だから、これを①に代入して、
$${V×360°=180°×(M+V-2)}$$
両辺を180°で割って、
$${V×2=M+V-2}$$
$${V×2=M+V-2}$$
$${M-V=2}$$
これで、証明は終わりです。
6 マイバッグを小さく折りたたむことができたのは
山折りと谷折りが集まる点は、すべて山折りと谷折りの個数の差が2なので、前川=ジュスタン定理より平坦に折りたたむことができる。
7 おわりに
今回は、平坦に折られたマイバッグから、折り紙に関する定理「前川=ジュスタン定理」を考えました。
ちょっとだけ難しい話をすると、今回は予め平坦に折られたマイバッグからこの定理を見つけたので、この定理は必要条件です。
平坦に折られている→前川=ジュスタン定理が成り立つ
では逆はというと、この定理が成り立っていても、平坦に折りたためるかどうかは分かりません。
実は山折りと谷折りが指定されている紙が平坦に折れるかどうかを判定することはNP困難であることが証明されています。
これは効率よく平坦に折れるかどうかを判定する方法が存在しない問題ということです。
折り紙については、他にも面白い定理がいくつもあります。
興味のある方は、この記事を書くにあたっての参考文献を掲載しますので、一度見てみてください。
折り紙に関する本なので、一般的な数学本よりもカラーの図解が多く楽しいです。
最後まで読んでいただき、ありがとうございました。

