
天才が考えたパズル
こんにちは。
今回は数学のパズルを1つ紹介します。
とても有名なパズルです。
必要なのは、「紙」と「ペン」と「ハサミ」と「粘り強く取り組む力」です。
これが一番難しい(笑)
1 問題
巡礼者の1人、小間物行商人が持っている下の絵のような正三角形を4つに切って、正方形を作ることはできるでしょうか?

この問題に取り組まれたい方は、記事を読むのをここで一度止めて考えられてください。
この後、答えを示します。
答えは前半(作図)と後半(ピースの移動)に分けます。
数学的なことを置いといて答えだけ確認したい方は、後半から見てください。
2 答え(前半)
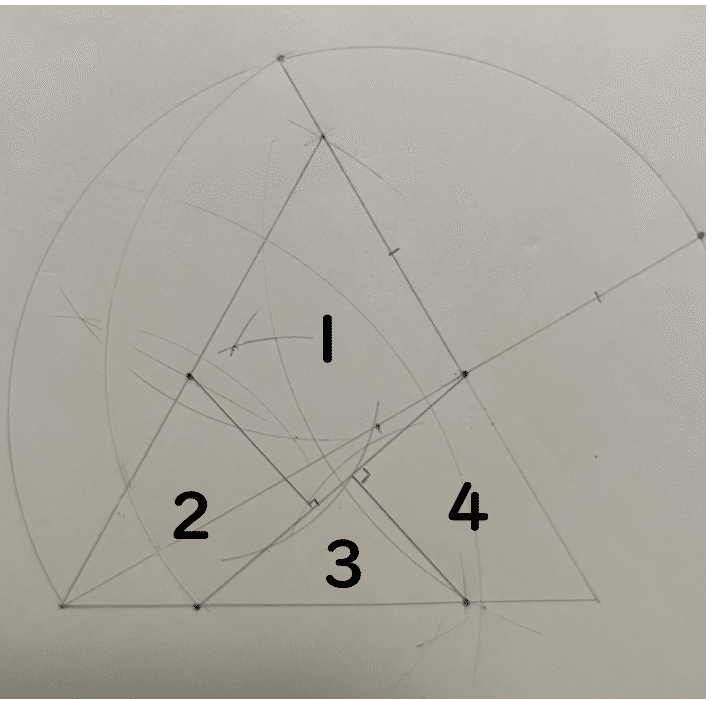
手順1
正三角形の2辺の中点をそれぞれ作図します。

手順2
正三角形の1つの頂点から、先ほど作った中点に向かって直線をひきます。(青矢印で示している)
その直線上に、通った中点からの距離が、正三角形の1辺の半分になるような点をとります。(下図赤矢印で示した点)

手順3
下の図のオレンジの線分の中点を作図する。

手順4
手順3で作図した中点を中心とする半円をかく。
また、正三角形の1辺を延長して、半円との交点をとる。(青矢印)

手順5
正三角形の1辺の中点(青矢印)を中心に、下の図のような弧をかき、正三角形の底辺との交点を作図する。(赤矢印)

手順6
下の図の青矢印の点と赤矢印の点の距離が、赤線と同じ長さになるように、赤矢印の点をとる。

手順7
下の図のような赤線をかき、その線に向かって青矢印の垂線をひく。

これで4つに分けられました。
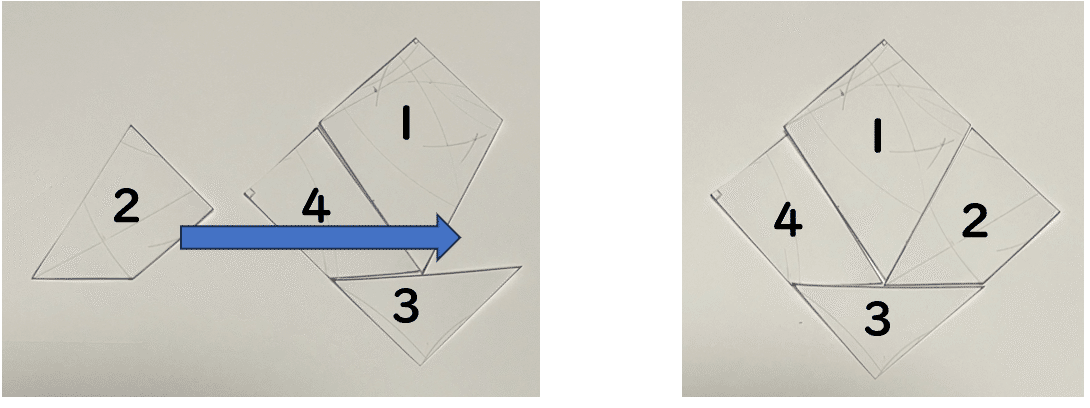
3 答え(後半)
「1」のピースを移動します。

「3」のピースを移動します。

「2」のピースを移動します。
これで正方形が完成します。
4 パズルの作者
このパズルの作者は、ヘンリー・アーネスト・デュートニーという現代パズルのルーツのような方です。
デュートニーは、サム・ロイドと同じ時代に生きた人ですが、この2人の捜索スタイルは対照的でした。
ストーリー仕立てで読者を楽しませるのがロイドのパズルで、面白さ・エレガントさを解答の中にまで持続させ、問題の裏に隠された数学的理論にまで読者を踏み込ませるのがデュートニーのパズルです。
5 今回のパズルに潜む数学
このパズルには、「ボヤイの定理」、「ヒルベルトの第3問題」、「3の4乗根の作図」をパズルの読者に触れさせたかったのかもしれません。
簡単に紹介します。
・ ボヤイの定理
平面上に面積の等しい2つの多角形が与えられたとき、どちらにも組み立てられる有限な面積をもつ三角形が必ず存在する。
イメージは、以下の通りです。

これが、どんな多角形にも成り立つというのがボヤイの定理です
証明は省略します。
興味のある方は、参考文献でユーチューブの動画を紹介しますので、そちらをご覧ください。
・ ヒルベルトの第3問題
同じ体積の多面体が2個与えられたとき、一方を有限個の多面体に切断して組み換えることで、他方を作ることは常に可能か?
これは、先ほどのボヤイの定理の立体バージョンです。
残念ながら、これは常に可能ではないことが証明されています。
・ 3の4乗根の作図
今回のパズルの最初に与えられた正三角形の1辺の長さを2とすると、面積は$${\sqrt{3}}$$です。
正三角形を正方形にできたとき、その面積は$${\sqrt{3}}$$です。
ということは、正方形の1辺の長さは$${^4\sqrt{3}}$$です。
6 デュートニーのすごさ
最初に紹介したパズルの問題は、次の通りでした。
巡礼者の1人、小間物行商人が持っている下の絵のような正三角形を4つに切って、正方形を作ることはできるでしょうか?
実は、上の太線部「4つに切る」というのがこの問題の難しいところです。
4つではなく、5つなら難易度が下がります。

そうすると長方形ができます

本当に正方形なの?と思う方もいらっしゃると思うので、これも参考文献に証明を載せておきます。
この最後の写真の右の正方形を見ると、最初の正三角形が5つのピースに分割されたのが分かります。
7 おわりに
デュートニーのパズルは、その裏に数学の定理が存在している場合があるからとても面白いです。
デュートニーは、正五角形を正方形に並べ替える問題についても考察しています。
とても面白いので、ぜひ調べてみてください。
参考文献
・ ガードナーの数学娯楽
・ 巨匠の傑作パズルベスト100
・ ボヤイの定理の証明
・ 正三角形を5つの小片に分割して正方形にできる証明
