
コメントから生まれた記事!!
こんにちは。
今回は、別の記事で頂いたコメントを基にした記事を作成しました。
記事が記事を生むというのでしょうか?
これは記事を書いた私としては、とても嬉しいことです!!
最後まで読んでいただけると、うれしいです!
1 頂いたコメント
以前書いた記事で、このようなコメントをいただきました。
https://note.com/yuzu_mathlove/n/n05544af90a50
ダビデの星とかソロモンの星は、図形にパワーがあると言われているようです。実験してみると自分のパワーが上がるような気がします。他にもそういう図形があるようですが、それは何故でしょうかね?
私はお恥ずかしいことに、「ダビデの星」や「ソロモンの星」というものを知りませんでした。
そのような幾何学模様があり、運気上昇に使われているということで、気になったため調べてみた次第です。
2 ソロモンの星
まずはソロモンの星です。
これは五芒星とも呼ばれます。(以下、五芒星)
「芒」とは、「のぎ」とも呼びます。
芒(のぎ)は、コメ、ムギなどイネ科の植物の小穂を構成する鱗片(穎)の先端にある棘状の突起のこと。
つまり、五芒星とは、5つの突起(芒)がある星のような図形ということです。
具体的には以下のような図形です。

外側にある正五角形(点線)の各頂点を1つ飛ばしで結んでできる図形になります。たしかに、5つの突起がある星のような図形です。
五芒星は、以下の歴史があるようです。
5つの要素を並列的に図案化できる図形として、洋の東西を問わず使われてきた。世界中で魔術の記号とされ、守護に用いることもあれば、サタニズムに見られるように上下を逆向きにして悪魔の象徴とすることもある。悪魔の象徴としてとらえる際には、デビルスターと呼ばれることもある。
私は、この図形には2つの美しさがあると思います。
・【美しさ1】黄金比
黄金比とは、人間が美しいと感じる比で、ピラミッドやモナリザなどの建造物や美術品、日本では名刺の縦横比などに見られます。
具体的には、黄金比は
$${1:\frac{1+\sqrt{5}}{2}}$$
という比になります。
実は、正五角形の1辺の長さを1とすると、1辺と対角線の長さの比は黄金比になります。

以下、黄金比の導出について記載します。
もし、数学が苦手な場合は飛ばしてください!!
1辺の長さが1の正五角形ABCDEがある。
対角線ADとCEの交点をF、AD=$${x}$$とする。

△ABCと△AEDは二等辺三角形で、正五角形の1つの内角の大きさは108°だから、
$${∠BAC=∠EAD=(180°-108°)÷2=36°}$$
これより、
$${∠CAD=108°-36°×2=36°}$$
同様に、
$${∠ACB=∠ECD=(180°-108°)÷2=36°}$$
これより、
$${∠ACE=108°-36°×2=36°}$$
$${∠BDC=∠ADE=(180°-108°)÷2=36°}$$
これより、
$${∠ADB=108°-36°×2=36°}$$

△CDFに注目すると、
$${∠CFD=180°-36°-72°}$$
$${=72°}$$
$${∠CFD=∠CDF=72°}$$で、2角が等しいから、
△CDFは二等辺三角形である。

△ACFに注目すると、
$${∠CAD=∠ACE=36°}$$
より、2角が等しいから、二等辺三角形といえる。

上のオレンジの三角形と青の三角形は二等辺三角形で、
$${CD=1}$$より、
$${CD=CF=AF=1}$$
である。
またAD={x}$$だから、
$${FD=x-1}$$である。

次に△ACDと△CDFに注目する。
この2つの三角形は、2角がそれぞれ等しいから、相似である。

相似な図形では、対応する辺の比はそれぞれ等しいから、
$${AD:CF=CD:DF}$$
$${x:1=1:(x-1)}$$
この比例式を解くと、
$${x^2-x=1}$$
$${x^2-x-1=0}$$
解の公式を使って、
$${x=\frac{1±\sqrt{5}}{2}}$$
$${x>0}$$より、
$${x=\frac{1+\sqrt{5}}{2}}$$
ということで、正五角形の1辺と対角線の比が黄金比になると示せました。
・【美しさ2】次々に正五角形を作れて、五芒星ができる
最初の正五角形(下の図だと、外側の正五角形)を基に五芒星を描くと、さらに五角形(下の図だと、赤い図形)ができます。
この五角形も正五角形です。
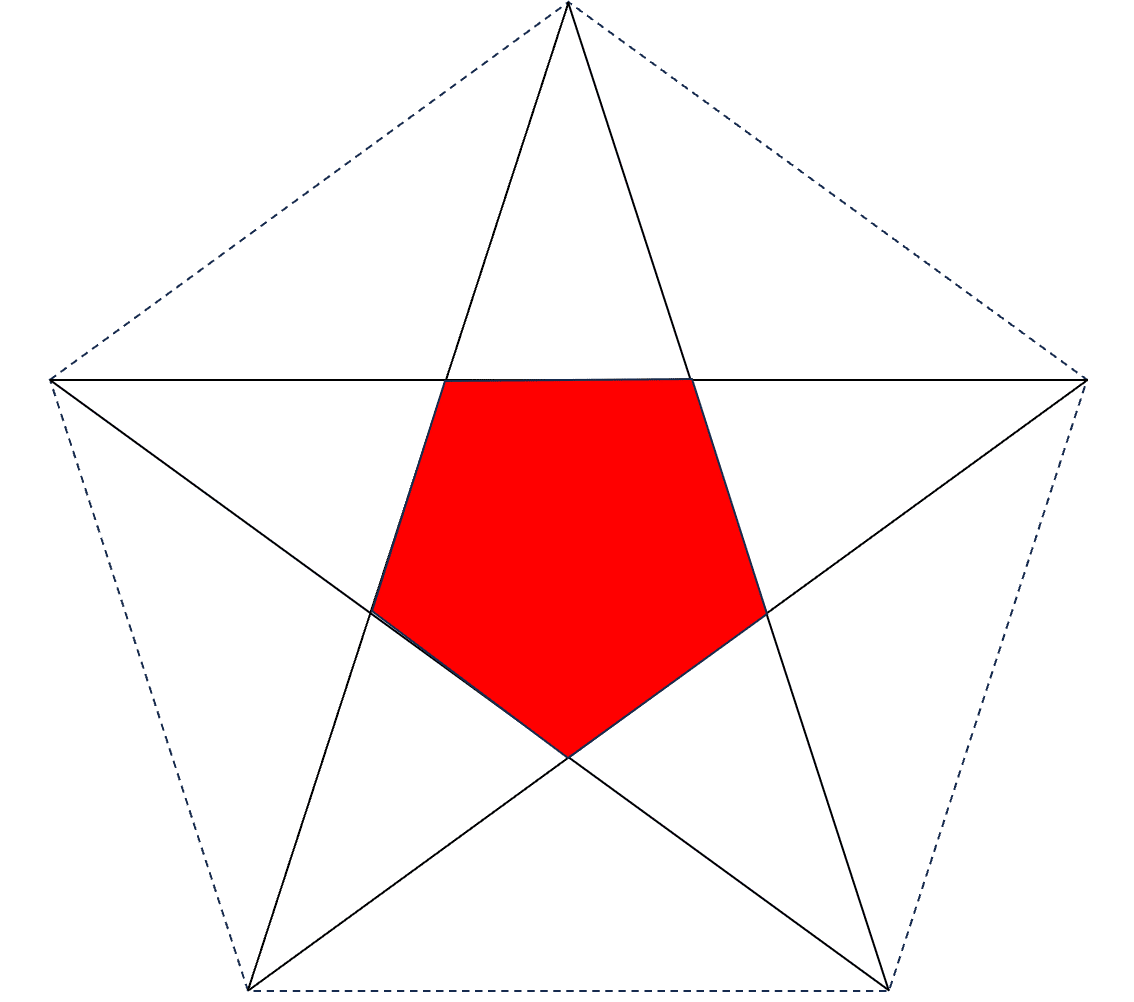
なぜ正五角形といえるかというと、上述したように赤い五角形の外角が全て72°だからです。

よって、この赤い正五角形を基にまた五芒星を描けます。

新しくできた五芒星の1辺(真ん中の正五角形の対角線)と真ん中の正五角形の1辺の比も黄金比です。
これを続けると、五芒星を5つ描けました。

この5つ全てに黄金比があると考えると、美しいなと思えます。
3 ダビデの星
ダビデの星は六芒星とも呼ばれる図形です。(以下、六芒星)
この図形は、正六角形の各辺を延長して作られる図形です。

以下は、ウィキペディアから引用しています。
このしるしは、古代イスラエルのダビデ王に由来するとされるが、歴史的に実在した実際のダビデ王との関連を示す証拠は無い。その起源についても様々な説が唱えられている。
日本でも、同様の「籠目」という文様がある。竹編みの籠の編み目を図案化したもので、魔除けとしてこの図形を用いることがあった。以前は伊勢神宮周辺にある石灯籠に籠目が刻まれていたが現在はすべて撤去され一基も現存していない(そもそも伊勢神宮の管理所有物ではない)。家紋としては籠目紋といい、「籠目」、「丸に籠目」などが使用されている。江戸時代には、小宮氏、曲淵氏などが用いた。
・ 【美しさ1】白金比
黄金比と同様に、人間が「美しい」と感じる「白金比」があります。
白金比とは、
$${1:\sqrt{3}}$$
です。
下の図のように、六芒星を作るための正六角形(赤い線の正六角形)の1辺の長さを1とします。
六芒星の各頂点を結ぶと、正六角形(黒い線の正六角形)になります。
この正六角形の1辺の長さは$${\sqrt{3}}$$です。(下の図参照)

次の項目でも述べますが、六芒星は次々に作れるため、次々に白金比になる正六角形が現れます。
ここに美しさがあります。
・ 【美しさ2】次々に六芒星が作れる
これは五芒星と同じ性質ですが、次々に六芒星が作れます。

小さくなると、汚くなります(笑)
この性質は、このような〇芒星に共通する性質なのかもしれませんね。
4 五芒星と六芒星が使われているもの
私が調べていて、「お~。すごい」と感じたのは、モロッコの100フラン銀貨です。
画像は著作権があると思うので、作ってみました。
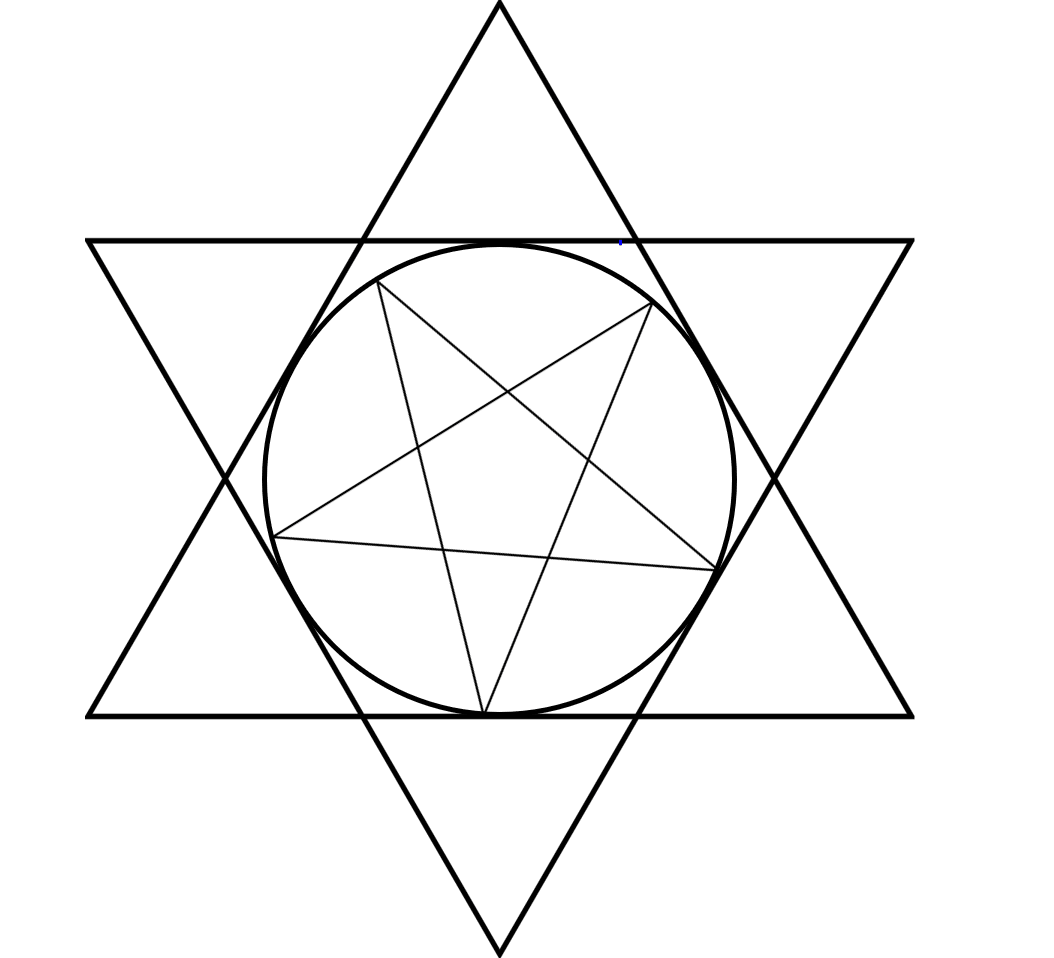
個人的に円があるのもいいですね。
5 おわりに
今回は、頂いたコメントを起点に、記事を書かせていただきました。
私の記事では、「不思議なパワー=図形的美しさ」と捉えて書いてみました。
昔から大切にされている印には、何か神秘的な美しさが秘められており、人間は本能的にそれに吸い寄せられているのかな?と考えてみた次第です。
今回、このような記事を書くヒントを与えていただいた読者様には、この場を借りてお礼申し上げます。
ありがとうございました!!
全ての疑問にはこの記事では答えられていないと思います。
その点は申し訳ございません(´;ω;`)ウゥゥ
また、最後まで読んでいただき、ありがとうございました!!

