見出し画像

”ど”文系人間がPythonで時系列分析(株価予測)に挑戦してみた。

YHの独り言

目次

１．はじめに
２．概要
３．実行環境
４．分析の流れ
５．分析の実践
６．最後に

１．はじめに

2022年10月より、Aidemy Premiumにて『データ分析講座』を3ヶ月受講しました。講座受講の成果物としてこの記事を掲載します。

私は金融系の企業に勤める"ど"文系の人間です。
数学は高校時代に諦めて以降ほぼ関わっておりません。"文系"とはいえ英語も扱えないのですが。。。

AIや機械学習の分野に飛び込んだきっかけは、勤務先でデータ利活用を狙う部署へ異動したことです。エンジニアとしてのスキルを求められているわけではないのですが、プロジェクトの企画立案や協力会社とのコミュニケーションをするにあたり、データ分析の概念だけではなく、具体的な実装方法をインプットする必要性を感じ、講座の受講を決意しました。

講座で学んだ内容を基に"ど"文系人間が株価予測に挑戦しましたので、最後までお付き合い下さい。

２．概要

今回はSARIMAモデルを用い、国内時価総額トップ/トヨタ自動車㈱の株価を予測します。
中期的な株価推移の予測を目的とし、毎月末の終値の数値を基に2024年12月末までの株価予測を行います。

Pythonの基本的な説明は割愛しますが、私と同じような経歴の方向けに分析の流れを出来るだけ分かりやすく記載します！

３．実行環境

環境：Google Colaboratory
Pyhon ver：3.8.16

４．分析の流れ

SARIMAモデルを用いた時系列分析は、以下の流れで進めていきます。

(1)データの読み込み
(2)データの整理
(3)モデルの決定
(4)パラメーターの決定
(5)モデルの構築
(6)データの予測・可視化

５．分析の実践

(1)データの読み込み

①データの取得
まず、使用するライブラリをインポートします。

＃ライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import itertools
from pandas import datetime

続いて、データを取得します。
今回は、Yahoo!finance から株価のCSVデータを取得します。
CSV形式の時系列データをpandasというライブラリを用いて読み込み、TOYOTA_stock_Sorceという変数(箱のイメージ)に格納します。

TOYOTA_stock_Sorce = pd.read_csv("/content/drive/MyDrive/成果物/7203.T.csv")

今回は2016年11月～2022年11月までのデータを取得しています。
取得したデータの中身は以下のイメージです。

TOYOTA_stock_Sorce　(先頭の5行のみ)

②使用するデータを抽出
(1)で取得したTOYOTA_stock_Sorceのうち、使用するデータを抽出します。今回は終値(Close)のみ使用するため、"Close"列のみ抽出し、TOYOTA_stockに格納します。

#終値の抽出

TOYOTA_stock=TOYOTA_stock_Sorce['Close']

③時間情報をインデックスにする
時間情報をpandasのインデックス(TOYOTA_stock_Sorceの左端の0,1,2…の部分)に表示させます。

#indexに期間を設定
index=pd.date_range("2016-11-01","2022-12-01",freq="M")

#indexをTOYOTA_stockのインデックスに代入
TOYOTA_stock.index=index

これでデータの加工ができました。
作成したTOYOTA_stockを使い、分析を進めていきます。

TOYOTA_stock (先頭の5行のみ)

(2)データの整理

①定常性とは
時系列分析を行うには、『定常性』が重要な概念になります。
定常性とは、時間によらずデータの確率分布が変化しないという確率過程の性質です。言い換えると、「時間の経過によらず一定の値を軸に、同程度の幅で変化する」ことを指します。

もし定常性を無視したデータを分析すると意味のない相関を検出する可能性があります。いわゆる疑相関です。「時間の経過」という共通要素により、無意味な相関関係を生んでしまう恐れがあるのです。

このように時系列分析を行う際は定常性のある時系列にしてから分析を進める必要があります。

②データパターンの確認
時系列に定常性を持たせる手法の一つに、季節調整があります。
基の原系列から季節変動を取り除いたデータを季節調整済み系列と呼び、StatsModelsのtsa.seasonal_decompose()を使用することで、トレンド・季節変動・残差(=原系列-トレンド-季節変動)に分けることが可能です。つまり、残差は定常性のある時系列データになります。
TOYOTA_stockのデータパターンを確認してみます。

#データパターンの確認
sm.tsa.seasonal_decompose(TOYOTA_stock,freq=12).plot()
plt.show()
上から原系列、トレンド、季節性、残差

トレンドと季節性があることが分かります。

③自己相関係数・偏自己相関
自己相関係数は、過去の値とどれほど似ているか、を示した値です。
一方、偏自己相関は、ある一時点のデータが前のデータと相関がある場合にその影響を取り除いて相関を求めたものです。
例えば、3日前→2日前→1日前→今日とデータを通じて相関している可能性があるため、この影響を取り除かれたものが偏自己相関です。
自己相関係数、偏自己相関係数を可視化します。

fig=plt.figure(figsize=(9,7))

＃自己相関係数の可視化
ax1=fig.add_subplot(211)
fig=sm.graphics.tsa.plot_acf(TOYOTA_stock,ax=ax1)

＃偏自己相関係数の可視化
ax2=fig.add_subplot(212)
fig=sm.graphics.tsa.plot_pacf(TOYOTA_stock,ax=ax2)

plt.show()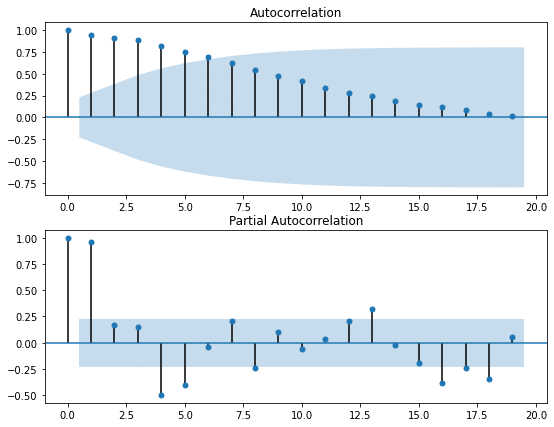
Autocorrelation:自己相関係数　Partial Autocorrelation:偏自己相関係数

(3)モデルの決定・データの周期の把握

(2)②でTOYOTA_stockにはトレンド・季節性があることが分かりました。よって、SARIMAモデルを採用し分析を行います。

【番外編：時系列分析のモデル】

・MAモデル(移動平均モデル)
過去の式と共通部分を持つため自己相関を持ち、過去の誤差に影響されるモデル。q期前までは自己相関を持ち、q＋1期前のデータとは自己相関を持たない、という性質を持ちます。

・ARモデル(自己回帰モデル)
直前のp個の値を用いて次の値を予測するモデル。過去の値から回帰的に値を推定します。

・ARMAモデル
MAモデルとARモデルを組み合わせたモデル。ARMA(p,q)と示す。

・ARIMAモデル
ARMAモデルへ原系列を階差系列に変換し適応させたもの。非定常過程にも適応可能。d時点前との差分をとったARMA(p,q)をARIMA(p,d,q)と表します。pを自己相関度、dを誘導、qを移動平均と呼びます。

・SARIMAモデル
ARIMAモデルをさらに季節周期をもつ時系列データにも拡張できるようにしたモデル。SARIMAモデルは(p,d,q)に加え、(sp,sd,sq,s)のパラメーターを持ちます。sは周期を示し、sp,sd,sqはそれぞれ季節性自己相関、季節性導出、季節性移動平均といいます。

(4)パラメーターの決定

①データの周期の把握
残念ながら、PythonにはSARIMAモデルのパラメーター(p,d,q)(sp,sd,sq,s)を自動で最も適切にしてくれる機能はありません。そのため、最も適切な値を調べるプログラムを書く必要があります。

ただし、パラメーターsは事前に調べる必要があります。
季節変動の周期は12なので、s=12とします。

②パラメーターの決定
情報量基準(今回はBIC/ベイズ情報量基準)によって、パラメーターの適切な値を調べるプログラムを書きます。
情報量基準とは、モデルの良し悪しを示す指標のイメージですBICの場合、数値が小さいほどパラメーターの値は適切です。

#(p,d,q)(sp,sd,sq)を求める
def selectparameter(DATA,s):
    p=d=q=range(0,2)
    pdq=list(itertools.product(p,d,q))
    seasonal_pdq=[(x[0],x[1],x[2],s) for x in list(itertools.product(p,d,q))]
    parameters=[]
    BICs=np.array([])
    for param in pdq:
        for param_seasonal in seasonal_pdq:
            try:
                mod=sm.tsa.statespace.SARIMAX(DATA,order=param,seasonal_order=param_seasonal)
                results=mod.fit()
                parameters.append([param,param_seasonal,results.bic])
                BICs=np.append(BICs,results.bic)
            except:
                continue
    return print(parameters[np.argmin(BICs)])

selectparameter(TOYOTA_stock,12)

＞実行結果
［（１，１，０），（０，１，１，12），735.2488255367572］

(5)モデルの構築

パラメーターを決定したので、早速モデルを構築します。『sm.tsa.statespace.SARIMAX(DATA,order=(p,d,q),seasonal_order=(sp,sd,sq,s).fit()』でモデルを構築し、SARIMA_TOYOTA_stockに格納します。
(p,d,q)(sp,sd,sq,s)は(4)②で取得したパラメーターを記入します。

#モデルの構築

SARIMA_TOYOTA_stock=sm.tsa.statespace.SARIMAX(TOYOTA_stock,order=(1,1,0),seasonal_order=(0,1,1,12)).fit()

(6)データの予測・可視化

モデル名.predict("予測開始時","予測終了時")により予測データが得られます。今回は、2020年11月～2024年12月までの予測結果を得ます。

TOYOTA_stock_pred=SARIMA_TOYOTA_stock.predict("2020-11-30","2024-12-31")
plt.plot(TOYOTA_stock_pred)
plt.show()
TOYOTA_stock_pred：2020年11月~2024年12月の予測結果


予測データを得られたので、元の時系列データと予測データを同時に出力します。

#元の時系列データと予測データの比較
plt.plot(TOYOTA_stock)
plt.plot(TOYOTA_stock_pred,color="r")
plt.show
元の時系列データと予測データ

青が元の時系列データ、赤が予測データです。同時に出力すると、予測データは、実際の時系列データよりも遅れて推移していることが分かります。
ただ、遅れてはいるもののデータの推移は凡そ合致しています。
SARIMA_TOYOTA_stockは、遅れて数値が推移するなど正確な予測には不適かもしれませんが、全体の動きを予測することはできそうです。

６．今後の課題

時系列分析を行ってみて、大きく2つの課題を感じました。

(1)モデルの選択
今回はSARIMAモデルを採用しましたが、別のモデルを使うことで更に精緻な予測ができるかもしれません。SARIMAモデル以外のモデルの学習もしたいと思います。

(2)株価予測するにあたり外部要因の反映
今回サンプルとして採用したトヨタ自動車㈱をはじめ、各企業は企業価値向上の為に多くのIR戦略を実施しています。自然言語処理を用い、各種企業情報のネガポジ分析も加えることで正確で且つタイムリーな予測が可能になるかもしれません。
また、トヨタ自動車㈱の株価には、為替相場や鉄鋼市場価格などが特徴量となる可能性もあります。もしかしたら予想だにしない思わぬ特徴量もあるかもしれません。こういった特徴量も予測に反映させると面白いですね。

７．最後に

Aidemyの講座の受講は大変いい経験でした。
AIや機械学習の概念のみならず実際にコードを書いて実践することで、データの成型やモデルの選択など、データ分析時の注意点を学ぶことができました。勤務先でのデータ利活用プロジェクトでも大いに活用したいと思います。

"ど"文系の私にとっては、正直に言って難しい内容もあり相応に時間がかかりましたが、それだけの価値がある時間でした。
私はまだ初心者中の初心者です。復習＆アウトプットを重ね日々学習を続けたいと思います。


この記事が気に入ったらサポートをしてみませんか？