『数式組版』を組む技術：ディスプレイ数式(1)

本稿において，“本書”とは木枝祐介著『数式組版』ラムダノート（2018）のことである．
>>> https://www.lambdanote.com/collections/mathtypo
また，本書はLuaLaTeXを用いて組まれた．したがって本稿ではLuaLaTeXの使用を前提としている．
本書が組まれた当時はTeX Live 2017が用いられたが，多くのコードはそれより後のTeX Live 2019まで共通して使用可能である．
本稿では，バージョンに強く依存する場合を除いて，各バージョンは明記されないことがある．

揃え

よくしられたように，LaTeXにおいて複数行からなるディスプレイ数式の記述は`eqnarray`環境によって実現するのが基本である．
つぎのコードは数式番号を出力しないように記述した例である（以降の例も同様に数式番号を出力しないものである）．

\begin{eqnarray*}
f(x) &=& ax^8 - bx^6 + cx^4\\
&& - dx^2 + e
\end{eqnarray*}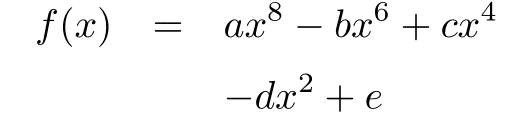

この出力は組版上の不備があるだけでなく，数学的にも不備のある出力になってしまっている．
これを補正する．
なお，なぜこの出力を不備とするのかの詳細は本書を参照のこと．

◆`eqnarray`の問題点
`eqnarray`は`latex.ltx`で定義されている．
よくしられたように，`eqnarray`には問題がある．
その問題のある点は次の箇所である．

\def\eqnarray{%
...
     &\global\@eqcnt\@ne\hskip \tw@\arraycolsep \hfil${##}$\hfil
     &\global\@eqcnt\tw@ \hskip \tw@\arraycolsep
        $\displaystyle{##}$\hfil\tabskip\@centering
...
}

`\hskip \tw@\arraycolsep`と`${##}$`とである．
くわしい挙動はここでは記さないが，この`\arraycolsep`の2倍というスペースが`&`/`&`で挟まれた，上の例でいえば等号（=）の両脇に入っている．
これを補正する必要がある．
つぎは局所的に`\arraycolsep`を0ptにした例である．

\begingroup
\arraycolsep0pt
\begin{eqnarray*}
f(x) &{}={}& ax^8 - bx^6 + cx^4\\
&& - dx^2 + e
\end{eqnarray*}
\endgroup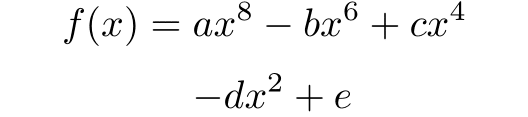

しかし，この出力状態でもまだ不備がある．
これも次のように局所的に対処することができる．

\begingroup
\arraycolsep0pt
\begin{eqnarray*}
f(x) &{}={}& ax^8 - bx^6 + cx^4\\
&& {}- dx^2 + e
\end{eqnarray*}
\endgroup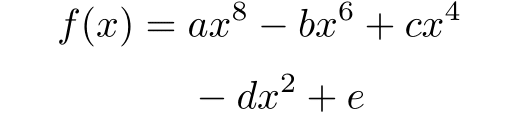

違いは，第2行目のマイナスの直前に`{}`を挿入している点である．
この操作は通常記号アトムを挿入していることに等しい．

なお，実際の運用時に毎回局所的に操作するわけではなく，`eqnarray`環境を適当に再定義してやることで対処するのが合理的である．

◆`amsmath`パッケージの利用
`amsmath`パッケージを利用する場合も安易な記述では不適当な出力となってしまう．

\begin{align*}
f(x) &= ax^8 - bx^6 + cx^4\\
& - dx^2 + e
\end{align*}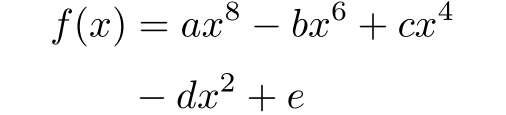

この不備のある出力を補正する．
「`&`の位置で揃えが行われる」これは事実で間違いなのであるが，単に等号（=）の後ろに記述しただけでは，つぎのようにまだ不備のある出力となってしまう．

\begin{align*}
f(x) =& ax^8 - bx^6 + cx^4\\
& - dx^2 + e
\end{align*}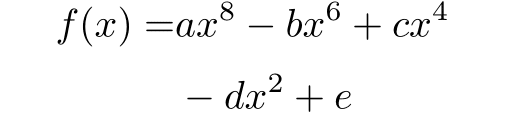

等号の大きさだけ不足していることを鑑み，つぎのようにしても適当な出力は得られない．

\begin{align*}
f(x) & = ax^8 - bx^6 + cx^4\\
& \hphantom{=} - dx^2 + e
\end{align*}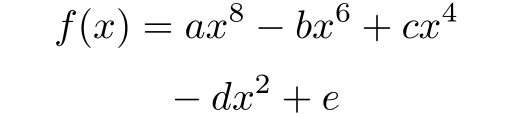

不足していたのは，等号まわりのアトム関係の処理である．
これを補いつぎのようにすることによって，ようやく適当な出力を得ることができる．

\begin{align*}
f(x) & = ax^8 - bx^6 + cx^4\\
& \hphantom{{}={}} - dx^2 + e
\end{align*}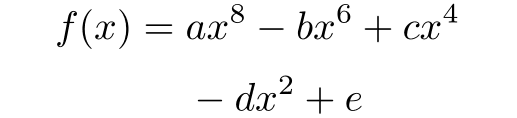

注：`amsmath`パッケージの提供する`align`環境は，かつて`eqnarray`のときと同様にさらに`{}`による処理が必要であったが，現在は`{}`による処理は不要となっている．