『数式組版』を組む技術：\leftと\right (1)

本稿において，“本書”とは木枝祐介著『数式組版』ラムダノート（2018）のことである．
>>> https://www.lambdanote.com/collections/mathtypo
また，本書はLuaLaTeXを用いて組まれた．したがって本稿ではLuaLaTeXの使用を前提としている．
本書が組まれた当時はTeX Live 2017が用いられたが，多くのコードはそれより後のTeX Live 2019まで共通して使用可能である．
本稿では，バージョンに強く依存する場合を除いて，各バージョンは明記されないことがある．

大きさの自動選択

よく知られたように，(La)TeXの数式モードにおいてパーレンなどをつぎのように`\left`と`\right`とをともなって使用することにより，(La)TeXが適当と判断した大きさが選択される．

\left(x\right)
\left(\frac{1}{2}\right)
\left(\sum_{i=1}^{n}A_{i}\right)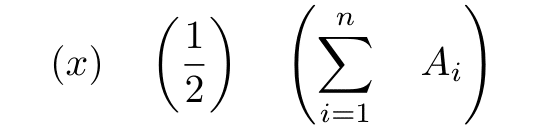

なお，選択される大きさは次のものにも依存するが，本稿では特にふれないことにする．

\delimitershortfall
\delimiterfactor

`\left`と`\right`とをともなって選択される記号の大きさは，しだいに大きいグリフが選択されるが，ある一定の大きさを超えると，ひとつのグリフでなく，複数のグリフの集合体である．
この選択や集合体はマクロではなく，フォント機構によって実現されている．

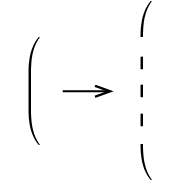
たとえば，`lmex10.tfm`を`tftopl`で得られる結果の一部をみるとのつぎのような記述がある．
`CHARACTER O 0`は「次」のグリフとして`NEXTLARGER O 20`を指定しており，`CHARACTER O 20`は「次」として`NEXTLARGER O 22`を指定しているというぐあいに，`CHARACTER O 40`まで選択され，`CHARACTER O 60`以降は，`VARCHAR`によってグリフの集合体として指定されている．
ここで，`TOP`グリフの集合体の上部分のグリフで，`BOT`はグリフの集合体の下部分のグリフを指定している．
`REP`がその間のグリフとして指定されている．

...
(CHARACTER O 0
  (CHARWD R 0.458336)
  (CHARHT R 0.039999)
  (CHARDP R 1.160013)
  (NEXTLARGER O 20)
  )
...
(CHARACTER O 20
  (CHARWD R 0.597224)
  (CHARHT R 0.039999)
  (CHARDP R 1.760019)
  (NEXTLARGER O 22)
  )
...
(CHARACTER O 22
  (CHARWD R 0.7361145)
  (CHARHT R 0.039999)
  (CHARDP R 2.360025)
  (NEXTLARGER O 40)
  )
...
(CHARACTER O 40
  (CHARWD R 0.79167)
  (CHARHT R 0.039999)
  (CHARDP R 2.9600315)
  (NEXTLARGER O 60)
  )
...
(CHARACTER O 60
  (CHARWD R 0.875003)
  (CHARHT R 0.039999)
  (CHARDP R 1.760019)
  (VARCHAR
     (TOP O 60)
     (BOT O 100)
     (REP O 102)
     )
  )
...
(CHARACTER O 100
  (CHARWD R 0.875003)
  (CHARHT R 0.039999)
  (CHARDP R 1.760019)
  (VARCHAR
     (TOP O 70)
     (BOT O 73)
     (REP O 76)
     )
  )
...
(CHARACTER O 102
  (CHARWD R 0.875003)
  (CHARDP R 0.600006)
  (VARCHAR
     (REP O 102)
     )
  )
...

この機構からわかるように，`\left`と`\right`とをともなったものは，常に適当なものが選択されるわけではない．
既に用意されているもののなかで，対象を超えるもののうちで最小のものが選ばれているにすぎない．
また，`\langle`や`\rangle`のような，グリフの特性上繰り返すグリフが指定できないものもある．
その場合は繰り返しの機構を用いることができず，必要な段階だけ事前にグリフを用意しなければならないことを意味する．

そういったいくつかの括弧類などを拡張するパッケージに，Latin ModernあるいはComputer Modernに使えるものとして，たとえばyhmathパッケージがある．
もちろんこのパッケージはターゲットとする書体が限定的であり，すべてを解決するものではない．
終局的には自らがグリフとフォントを用意することになる．

参照：
> texdoc yhmath