MEGABIGで期待できる収益を簡単にシミュレーションしてみた

2024年9月2日 00:07

昨日、今回（第1476回）のMEGABIGのことをTwitterで知った。
その回のMEGABIGは台風10号の影響でサッカーの試合が12試合中4試合中止になったため、普段よりも格段に当たりやすくなっているらしい。（MEGABIGは中止になった試合は的中判定になる。4試合中止までは開催する）

toto MEGA BIGが熱い。
対象の12試合中4試合が中止（自動的中扱い）なので、8試合分当たれば1等というレイドイベント発生。現在キャリーオーバー61億円。
公営ギャンブルとしてはありえない期待値。
なおtoto BIG/100円BIGは5試合中止のため額面払戻確定
— 極東の珍獣 (@ashikagunso) August 30, 2024

この情報を知ったのは購入可能期間が過ぎてからなので、そもそも手を出すことはできなかったのだがちょっとだけ気になったのでpythonでさくっと収益のシミュレーションをしてみようかなと思った。

収益の期待値などはTwitterで複数人が計算してあげているが、どの程度の分散があるのかを示している人はあまりいなかった（1等のみを考慮したポアソン分布を出している人はいたが）。

ということで、どれくらいのばらつきがあるのかを知りたいが、〇等賞と複数あってそれぞれ配当金が異なっているなど、分布を考えるのが結構めんどくさそう…ただ問題自体は単純なので、pythonで簡単に乱数によるシミュレーションを実装して結果を見てみた。

コードは以下の通りで、各当選の配当金はさらに下に貼ったツイートのものを参考にしている。

※ ちなみに、このプログラムでは自身が購入した口数によって変化する配当金について考慮していないので、極端に大きな口数でシミュレーションをすると現実の収益と乖離してしまうことに注意。

import math
import random
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from tqdm import tqdm

sns.set_theme()

LOOP = 1000
TICKET_NUM = 100000

# Default
# def _prob(rank: int) -> float:
#     n = 13 - rank
#     return math.comb(12, n) * (0.25 ** n) * (0.75 ** (12 - n))

# No.1476
def _prob(rank: int) -> float:
    n = 9 - rank
    return math.comb(8, n) * (0.25 ** n) * (0.75 ** (8 - n))

probabilities = {
    1: _prob(1),
    2: sum([_prob(i) for i in range(1, 3)]),
    3: sum([_prob(i) for i in range(1, 4)]),
    4: sum([_prob(i) for i in range(1, 5)]),
    5: sum([_prob(i) for i in range(1, 6)]),
    6: sum([_prob(i) for i in range(1, 7)]),
    7: 1.1
}

# ref: https://x.com/conferencesix/status/1829824896064766381
profit: dict[int, int] = {
    1: 28662869,
    2: 300,
    3: 300,
    4: 300,
    5: 300,
    6: 300,
    7: 0
}

def get_ticket_profit() -> int:
    """
    Generate a ticket profit based on the probabilities.
    """
    random_number = random.random()

    for rank, prob in probabilities.items():
        if random_number < prob:
            p = profit[rank]
            return p

    raise ValueError("Invalid probabilities")


def simulate(n: int) -> int:
    """
    Simulate n tickets and return the winning ranks.
    """
    return int(sum([get_ticket_profit() for _ in range(n)]))


if __name__ == '__main__':
    ps = []
    for _ in tqdm(range(LOOP)):
        ps.append(simulate(TICKET_NUM))
    fig1, ax1 = plt.subplots()
    ax1.hist(ps, bins=50, rwidth=0.8, log=True)
    fig1.savefig("hist1.png")
    pd.Series(ps).describe().to_csv("describe.csv")

今回のmega bigの期待値算出
最低配当が300円という裏ルールが適用される為、5等・6等に割り当てられた配当額を超えてしまう。その場合、上位配当のプールから捻出することになり今回のmega bigでは2等まで全て配当が300円となり、 1等の配当金も一人当たり330万円減ることになるみたい。 pic.twitter.com/NYIBWe8mxV
— たんじろ (@conferencesix) August 31, 2024

プログラムに書いている設定は以下のみで、その他の当選確率や配当金などはポアソン分布を仮定して計算したり、ツイートを参考にしたりしている。

自身の購入する口数：100,000 口
試行回数：1,000 回

上記の設定を分かりやすく言うと、3,000万（一口300円のため）をぶっこんだ人を1,000人用意してその結果を見てみようって感じ。

ではまず収益の分布を見ていく。
結果はポアソン分布のような形状になっており、収益が3,500万円付近に最頻値を持つ単峰性の分布となっている。ただ特徴的なのは各区間の間隔で、それぞれの区間は2,500万円ほどの間隔が均等に開いており、非常に疎なグラフとなる。

間隔の間に頻度の低い値も存在するか見るために対数軸にしてみたが、そういった値は無いため間隔の中には全く値が存在しないことが分かる。

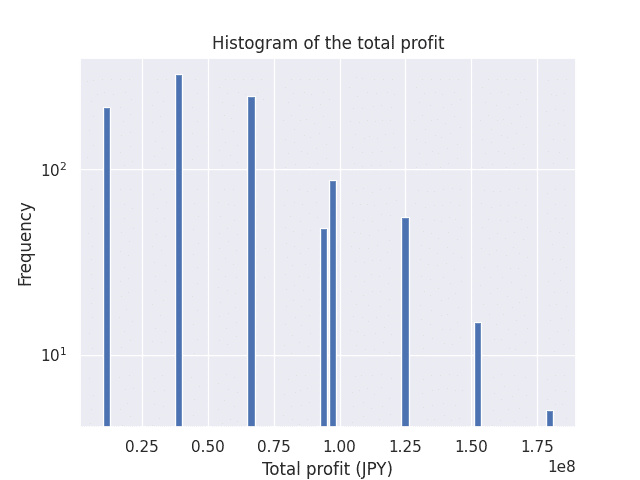
このままでは割合が見にくいため、縦軸を対数軸ではなく、なおかつ、割合の分布にしてみる。そうしてみると、およそ35%の確率で掛金の3,000万円とほぼ同じで、20%の確率で1,000万円になってしまうリスクが存在していることが分かる。Twitterでは「〇%で全損するので博打だ」という意見もちらほら見えるが、実際は2等以下も相当数当たることが予想できるため、全損の可能性は限りなく低い。

ちなみに、この粒度のグラフでは各ポイントが1本のデータに見えてしまうが、あくまでこれはヒストグラムのため範囲とビン数によって見え方が分かってくる。例えば、一番左の区間にズームアップしてみてみるとこのように、一つのデータに見える区間の中にもばらつきがあることが分かる（範囲は940万円から960万円までに適当に決め打ちした）。ただ、1等の配当金が他の等賞に比べて大きすぎるため、単一の区間にばらつきが収まって見えてしまっているだけだ。

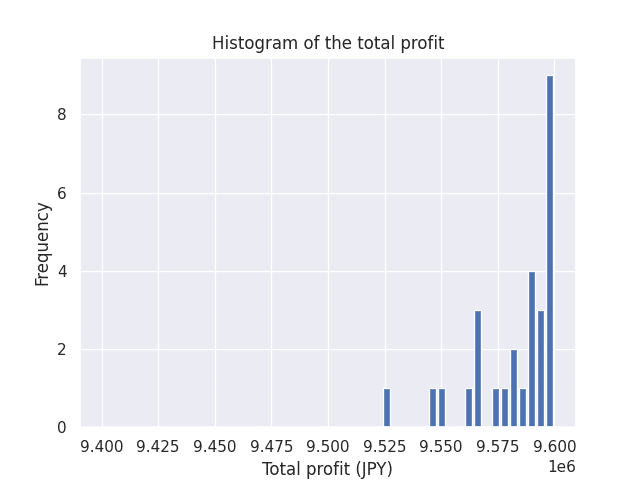
あと、すべてのデータの統計量は以下のような感じで、改めて数値で標準偏差を見ると非常にばらつきの大きい収益であることがうかがえる。

平均　　：　54,471,188.22
標準偏差：　34,886,007.98
最小値　：　9,524,100
25%　　：　38,260,319
50%　　：　38,352,419
75%　　：　67,006,738
最大値　：　181,665,114

最小値はおおよそ1,000万円と思ったより破産リスクは無いように思えるが、標準偏差が平均の6, 7割ほどあることからばらつきは非常に大きいことが分かる。ただ、平均（期待値）は5,400万円と掛金の1.8倍ほどになっているためリターンは非常に大きい。

でも、いざ自分が数千万持っていたとしても、やるかと言われたら絶対にやらない。自分の中では、数十%の損失が現実的（5%以上かな）に出るようなものは投資ではなくギャンブルだと思っていて、心配性だしギャンブルには弱いのでやろうとは思わない。

ただ、掛金が大きくなってくると話が変わってくるのだろうなと思う。例えば、掛金が1億円（333,333口）で同じように分布と統計量を出してみる。

平均　　：　179,182,965.87
標準偏差：　65,734,269.01
最小値　：　32,099,400
25%　　：　118,272,507
50%　　：　175,453,645
75%　　：　232,668,983
最大値　：　404,724,197

1億円をかけるとそもそも損をする可能性が2%未満で、98%の確率で利益を得ることができる。また、中央値が1.7億円程度のため、50%の人は7,000万円以上の利益を短期間で出せるようになるため、これは投資として間違いではないように思える。

補足

全体を通しての補足だが、そもそもTwitterで期待値を出している人やこのシミュレーションは宝くじの割り振り（？）に偏りがないものと仮定している。MEGABIGではくじを購入すると自動的に試合の合計得点の予想結果が生成されるが、それが一様分布でなく偏りがあった場合に、予想結果の被りが大量発生してしまい予測とも乖離してしまう。

まあ、そもそも宝くじの運営が統計的に負けるような仕組みにはなっていないと思うので、流石に偏らせるメリットがそこまで大きくないはず。なので、上記のはただの杞憂だとは思うが…

この記事が気に入ったらサポートをしてみませんか？