Factorization Machinesについて
1.Factorization Machinesの概要
全体紹介したMatrix Factorizationについてですが、
Matrix Factorizationは
ユーザーとアイテムの評価値行列から、特異値分解(SVDとは少し異なる)して未評価の値を予測するものでした。
これにはコールドスタート問題というのがありまして、実際に評価されたアイテム(明示的な評価)のみを考慮しており、暗黙的な評価は扱っていないところです。
例えば、新しく追加されたアイテムに関しては当然購入している人もいませんし、アイテムの評価もつけようがありません
つまり、既存のアイテムのみにしかこのアルゴリズムは使えない訳です。
これがコールドスタート問題と言われております。
そこで、Factorization Machinesというアルゴリズムが提案されました。
現論文
https://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf
Matrix Factorizationでは、2つの特徴量のみの交互作用のみしか扱うことができないことが一つの課題でした。
FMは暗黙的なデータや年齢や性別といった特徴ベクトルも考慮に入れることができ、それぞれの交互作用を加味したアルゴリズムとなっております。
2.FMの数式理解
下の図がFMのデータの持ち方になっております。

各列が特徴量の値となっております
次はFMの予測誤差の算出の仕方になっております

左項はlinear regressionで右がそれぞれの特徴量の交互作用を用いています
i:特徴量の数
n:ユーザーの数
<fi,fj>に関しては

となっており、kは因子数になっております。
xixjについては実際の値が0でない場所のみの交互作用をとってきております(Matrix Factorizationと似ていますね)
そのため、更新されるのは
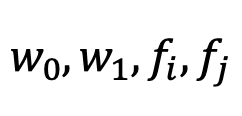
この4つとなります。論文では、それぞれをSGDで更新する形と記載されております。

3.まとめ
このアルゴリズムの強みはなんと言っても
コールドスタート問題が解決されることです
各特徴量にどのアイテムのページに何秒訪れたかなどを特徴量とすれば、新規のアイテムに関しても評価を行うことができます。
H&Mなどの日々アイテムが変わるようなサイトはこのアルゴリズムがとても有効に働くかもしれませんね。
それではまた。
この記事が気に入ったらサポートをしてみませんか?
