レコメンドエンジンのまとめ

1.レコメンドとは？

現在のYoutubeやNetflix、Amazonでは、さまざまなおすすめの動画や商品、「この商品をチェックした人はこのアイテムを購入しています。」などといった興味が引きそうな広告を見ないだろうか？

私たちがそのサービスで
・購入している情報
・商品のレビュー情報
・該当商品のページに訪れた
などの情報は、ユーザー体験を向上させるために推薦システムに利用されております。

現に、Netflixに関しては驚くことに推薦システム経由の視聴が80％
とかなり高い数値を出しております。
(Youtubeに関してはおよそ35％とされているそう)

対して、ニュースアプリについては
時系列的に最新のニュースをおすすめすれば見られるといった傾向もあり、

サービスによって、推薦システムは全く異なるものなのです。

これから様々な推薦システムについて紹介していきたいと思います。

2.ユーザーの評価の違いについて

ユーザーの評価には大きく２つの種類が存在します。

一つ目は、
明示的な評価(explict feedback)です。
これはユーザーが明示的に評価したことを指します。
例えば、あるアイテムにおける5段階評価などを指します。

二つ目は、
暗黙的な評価(implict feedback)です。
これはユーザーが直接評価したものではなく、あるアイテムのサイトを見た回数などのユーザー行動履歴からアイテムに対する関心を推定して嗜好データとする方法です。

この二つをしっかり区別してアルゴリズムを用いる訳なのですが、まずはこの二つの評価について、特徴をまとめました

3.評価方法

アルゴリズムの説明に入る前に、推薦システムにおける評価指標にはどういったものがあるか簡潔に説明します。

3.1 Precision@K

ユーザーにK個アイテムをおすすめしたとしたときに、その中に実際に好きなアイテムがどのくらいの割合であったかという指標になります。

3.2 Recall@K

再現率と同じようなもので、ユーザーにK個アイテムをおすすめしたときに、ユーザーの好きなアイテム群のうち何個当てることができたかという割合になります。

この２つの値を各ユーザーごとに算出し、その平均を評価指標にしたりしています。

実際には、必ずしも評価値があるわけではないため、
クリック数や購入したかしてないかなどの回数を利用したりしているそうです。

4.アルゴリズムの紹介

ここからは、簡単なアルゴリズムから順を追ってアルゴリズムの紹介をしていきたいと思います。

4.1　ランダム推薦

その名の通り、ランダムにアイテムを推薦するものになっております。基本的にはあまり用いられることはないのですが、のちに出てくるMatrix Factorizationなどのアルゴリズムでは
多様性が存在しない（のちに詳しく説明します）という問題が生じております。それが存在するという意味においては、
完全に意味のないアルゴリズムではなさそうです。

4.2　統計情報や特定のルールに基づく推薦

こちらも名前の通りの推薦になります。例えばこのような推薦方法があったとします。

・直近1ヶ月の売り上げ数がトップのアイテムを推薦する
・ユーザーの年齢や特定の属性情報に基づいて、アイテムを推薦する

このような年齢や売り上げ個数などの情報はサービス提供側で保持していることが多く、比較的扱いやすいデータです。

先月の売り上げ順であれば一番上推薦されているアイテムは先月一番売りあげたアイテムであり、ユーザーによってとてもわかりやすい推薦理由は売り上げに向上に繋がるので、無視することはできません。

ただ、明示的にユーザーの属性情報が入力しているとは限りません。
Amazonの用に明示的に自らの性別を入力することをないかもしれません。

また、別の問題としてマッチングサービスのような比較的ユーザーが能動的にプロフィールを入力することがあっても、自分をよく見せようとして誤った情報を入力したりと正しい予測ができない場合もあります。

ユーザーの年齢や性別などの人工統計学的なデータに基づいてアイテムを推薦することをデモグラフィックフィルタリングと言います。

この推薦システムを使うことには大きな問題点が他にあります。

例えば、性別ごとに推薦システムを変えるなどは
男性だからこれ
女性だからこれ
などというようにジェンダーレスの世の中で、公平性が欠けてしまう
ことがあります。

そのため、この推薦システムを使う際は注意しておかなければならないですね。

今回は、単純に全体的に評価が高いものを推薦するシステムとし、
10件をおすすめするとします。

また、既にユーザーが評価したものは推薦対象から除くものとします。

注意する点としては、評価数がかなり少なく評価が高いものだったり低いものには注意することです。

評価数が少ないと評価値の信頼性に欠けるため、今回は評価数が100以上存在するもののみを推薦システムに組み込みます。

4.3 アソシエーションルール（アプリオリアルゴリズム）

協調フィルタリング推薦の中でも、昔から現在まで幅広い業界で活用されています。

具体的な手法は、購買履歴データから
アイテムAとアイテムBは同時に購入されることが多いといった法則を見つけることです。

これに大事になってくるのが、
支持率と確信度とリフト値になります。

例えばこんな売り上げデータがあったとします

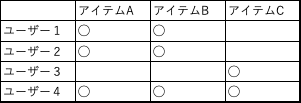
これでいう支持率というのは
アイテムAが出現した割合になります
（Aの出現数）／全データ数　＝ 3/4 ＝  0.75
ということになります。理解しやすいですね

同時出現数も計算していきます
ここではAとBが同時に出現してきた割合を出していきます。

支持度（AandB）＝　（AとBの出現回数）／　全データ数　＝0.75

この同時出現回数はリフト値を出す際に使います。

次に確信度になります。
確信度とは、アイテムAが出現した時にアイテムBが出現する割合になります。ベイズの定理みたいな感覚でしょうか。

確信度（A＞＝B）＝（AとBの同時出現回数）／（Aの出現数）＝
3/3 = 1.0

リフト値については、アイテムAとアイテムBの出現がどのくらい相関しているかを表すものになっています。

リフト値 = (支持度AandB）/（（支持度（A）＊支持度（B））

分子が大きくなればなるほどリフト値が大きくなるので、二つのアイテムは相関していることがわかります。

また、このリフト値の対数をとるとPMI（自己相互情報量）と呼ばれるものになります。
word2vecというアルゴリズムでもそれを要素とする行列を行列分解したものになることが知られております。

リフト値を使って、最適なアイテムを推薦するものが
アプリオリアルゴリズムというものになっております。

ただし、アイテムの数が多すぎるとリフト値の計算にかなり時間が経ってしまいます。
そのため、あるアイテムの支持率が超えたものに限定して、
アルゴリズムを組むものがアプリオリアルゴリズムとなっております。

4.1．特異値分解（SVD:Singular Value Decomposition）

次は行列分解について紹介します。

左側にあるのが元の評価値行列と言われるものです。
これを
Uというユーザー因子行列
Vというアイテム因子行列
に分解させます。

kは潜在因子数(数学的には特異値)と呼ばれており、アルゴリズム作成の際はこれはハイパーパラメーターとなっております。

基本的には因子行列は説明ができないものとなっております。
例えばk=2とし、ユーザー数をmとした場合、U行列はm*kとなります。

1列目(k=1)の要素はファンタジー度合い
2列目(k=2)の要素はアクション度合い
が好きな要素だとします。

そうすることで、因子行列を使うことでベクトル空間を使って表現することができます（kが2または3の場合のみ）

ただし、先ほど述べた通り因子行列の各列の要素は基本的には説明ができないものになっています。

このUとV.tの内積はm*nとなり、元の評価値行列と同じになり、値が元の評価値行列と近似されることになります。

このように簡潔にSVDを紹介しましたが、
レコメンドにおいてはそのままSVDを使うことはほぼありません。

その代わりにSVDを実際のレコメンドに応用させることができたMatrix Factorization
というアルゴリズムを説明していきます。

4.2. Matrix Factorization(明示的な評価値に対する行列分解)

ここからようやくレコメンドの機械学習に近づいたのではと思います。
先ほど説明したSVDでは、未観測の場所においては欠損値保管をしなくてはいけませんでした。

ただし、今回説明するMatrix Factorizationに関しては欠損値を埋めることなく、観測された評価値だけを使って行列分解する手法を取ります。

実際にも、Netflixが主催した映画の評価値を予測するコンペティションでは、MFを用いた手法が提案され、成果を残しました。

求めたい最適化問題はこちらになります。

話を戻すと、結局求めたいのは上の因子行列になります。
つまり、因子行列の各要素を求めたいわけですよね。
ここで、勾配降下法を用いて各要素の偏微分を求めます。

これが各要素で勾配降下法をした場合の更新式になります。

ここで、ru,vは
実際の観測値であり
puとqiベクトルは内積をとっており、実測値のru,vとの差の誤差を最小にすることを目的としています。
第二項については、正則化項（L2ノルム）であり、過学習を抑制しております。

ここで肝になってくるのが、未観測の値についてはこの式を適用しないことです。これがSVDとの大きな違いです。

直感的に説明すると、未観測の値を仮に0にした場合、その0の値と初期にランダムに設定した各因子行列の対象箇所の内積が最小になってしまいます。

未観測は必ずしも嫌いだから見ていない訳ではなく、そもそも存在を知らないから見ていない訳です。

そのため、変に欠損値補完した0との誤差を最小にするのは意味が全くありません。

このMatrix Factorizationは、BigqueryやSparkにも実装されています。

4.3.暗黙的な評価に対する行列分解  (implict Matrix Factorization)

先ほどのMatrix Factorizationは、明示的な評価に対する行列分解で適用できるものになります。
第二章で説明しましたが、暗黙的な評価の方が実際にはデータとしては取りやすいです。

そのため、暗黙的なデータに対しての行列分解も存在します。

例えば、各アイテムごとにサイトが異なっていたとします。
アクセスログから、どのユーザーがどのアイテムのサイトにアクセスして
何回訪問したのかがわかるとします。

ruiは、そのサイトに訪れた回数になってます。
rui_barは、そのサイトを一度でも訪れれば1とする二値変数とします。

また、ruiの回数が多ければ多いほどそのアイテムに好意を頂いてることを仮定し、このような好意度の式を与えます。

一度でも見なれば1、見た数だけCuiが大きくなります。

ここで、暗黙的な評価に対する行列分解の最適化問題は

となります。明示的な場合と似ていますが、
これは全ての行列に対して計算を行います。また、Cuiを導入することで、好意度も考慮に入れていることがわかりますね。

また、Cuiのαとλに関しては、ハイパーパラメーターなので
データによって変える必要があります。

データが明示的なのか、暗黙的なのかしっかりとわかった上で、アルゴリズムの選択を行なっていきましょう。

5.次回のアルゴリズム説明について

MatricsFactorizationはとても様々な場面で用いられています
また、次回説明する
BPR(暗黙的に評価したアイテムと未評価のアイテムを考慮したアルゴリズム)
もMatrics Factorizationの派生と言えます。

また、Factorization Machinesというアルゴリズムについても説明していきたいと思います。

簡単に説明すると、ユーザーの様々な属性情報（年齢や性別）や映画の評価など様々な情報を扱うことによって、コールドスタート問題に対処できるメリットがあるアルゴリズムになっております。

最後には、MatrixFactorizationを深層学習化したアルゴリズムも紹介していきたいと思います。

自分の学習日記でもあるので、もし違うなどの指摘があれば教えてください笑
それではまた。