
【岐阜県公立高校入試】2022数学 解説
2022年3月3日に実施された岐阜県公立高校入試(第1次選抜)の数学について解説を公開します。
※問題は各自で入手してください。
1⃣は小問集合です
(1)正負の計算です(1年)。
$${6-4×(-2)=6+8=14}$$
です。積を先に計算しましょう。答えが -4 になった人は要注意です。
(2)文字式の計算です(1年)。
$${3(-x+y)-(2x-y)=-3x+3y-2x+y=-5x+4y}$$
です。( )を正しく外しましょう。
(3)文字式への代入です(3年)。$${x=5+√3}$$、$${y=5-√3}$$ のとき、式$${ x^2+2xy+y^2}$$ の値を求めます。そのまま代入しても解けますが、そんな「日向君の強引なドリブル」のような解き方をしていては、高校入学後に若林君に止められてしまいます。この問題は、
$${x^2+2xy+y^2=(x+y)^2}$$
と変形して、$${x+y=10}$$ を代入することで、$${10^2=100}$$ と解きます。
(4)さいころの確率です(2年)。出る目の積が5の倍数になる確率です。
「2個のさいころには1から6の数字がひとつずつ書かれており、どの目が出る確率も同様に確からしい」と問題文に書いていないため解答不能ですが、仕方がないので解きます。
5 (1,5)(5,1)
10 (2,5)(5,2)
と考えていけば、30までに12通りありそうですが、25のみ(5,5)の1通りとなるため、確率は、$${\frac {11} {36} }$$ となります。
(5)連立方程式です(2年)。
$${5x+2y=4}$$ かつ$${3x-y=9}$$ です。代入法でも加減法でも好きな方で解きましょう。$${x=2}$$,$${y=-3}$$ となります。連立方程式の解には、{ をつけ忘れないようにしましょう。
(6)立体の体積です(1年+3年)。
正四角すいの投影図が書かれており、底面は1辺6cmの正方形、正面から見るとは1辺6cmの正三角形となっています。立体の高さは正三角形の高さと等しいので、三平方の定理から、3√3cmとなります。
体積は、
$${6×6×3√3÷3=36√3}$$ となり、36√3㎤ です。
2⃣は2次方程式です(3年)
$${x^2+ax-8=0}$$ について解きます。
(1)$${a=-1}$$ のとき、2次方程式は、$${x^2-x-8=0}$$ となり、2次方程式の解の公式を用いて、
$${x=\frac{1\pm\sqrt{33}}{2}}$$
です。
(2)$${x=1}$$ が解の一つである場合、
(ア)$${x=1}$$ を代入して、$${1+a-8=0}$$ から、$${a=7}$$
(イ)このとき、$${x^2+7x-8=0}$$ を解くと、他の解は、$${x=-8}$$
3⃣はヒストグラムの問題です(1年)
(20人の)バスケットボール部員が5回ずつシュートをして成功した回数を人とグラムで表しています。
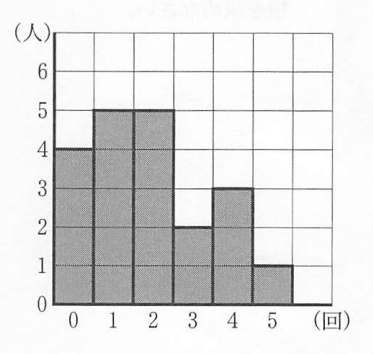
(1)人数は、$${4+5+5+2+3+1=20}$$ で、20人です。
(2)平均値は、$${(5+10+6+12+5)÷20=38÷20=1.9}$$ です。
(3)一人のデータを追加することで、平均値と中央値が一致します。
新しく加わるデータは、0から5のいずれかです。元の中央値は2ですが、新しいデータが加わったとき、0~5のいずれのときも、中央値に変動はありません。したがって、平均値が2になればよく、$${21×2=42}$$ から、$${42-38=4}$$ となるので、花子さんの成功した回数は4回となります。
4⃣は関数です(3年、2年)
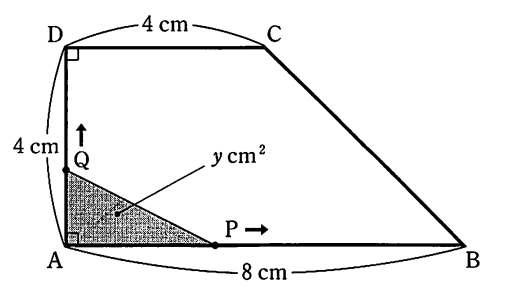
台形の辺上を2点P、Qが一定の速さで移動したとき、x秒後の△APQの面積をyとします。点Pは毎秒2cmでA→B→A、点Qは毎秒1㎝でA→D→Aと移動します。
(1)表中の空欄を埋めます。
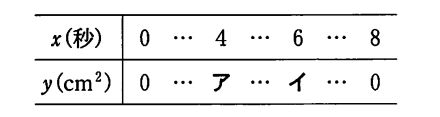
(ア)4秒後は、点Pが点B、点Qが点Dにいますので、△ABDの面積と等しくなります。$${8×4÷2=16}$$ から、アには16が入ります。
(イ)6秒後は、点Pが点Bから戻ってきて、辺ABの中点におり、点Qは点Dを通過して、辺CDの中点にいます。点Qが辺CD上にいる場合、△APQの高さは4㎝で一定となるので、AP=4㎝から、△APQ=$${4×4÷2=8}$$ イは8です。
(2)(ア)$${0≦x≦4}$$のときは、AP=$${2x}$$、AQ=$${x}$$ となり、
$${y=2x×x×\frac 1 2=x^2}$$ となります。
(イ)$${4≦x≦8}$$のときは、底辺がAP=$${(16-2x)}$$、高さが4㎝で一定 となり、
$${y=(16-2x)×4×\frac 1 2=-4x+32}$$ となります。
(3)グラフは、以下のようになります。
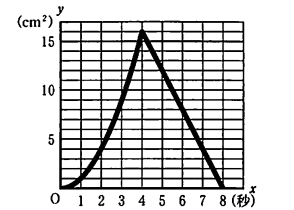
(4)△APQの面積と、台形ABCDから△APQを除いた面積の比が、3:5になる時を考えます。台形ABCD=$${(4+8)×4÷2=24}$$なので、3:5に分けると、△APQ=9になります。
$${0≦x≦4}$$のときは、$${x^2=9}$$ $${x=±3}$$ $${x=3}$$
$${4≦x≦8}$$のときは、$${-4x+32=9}$$ $${x=\frac {23} {4}}$$
以上から、3秒後、$${\frac {23} {4}}$$(5.75)秒後の2つです。
5⃣は図形の問題です(3年)
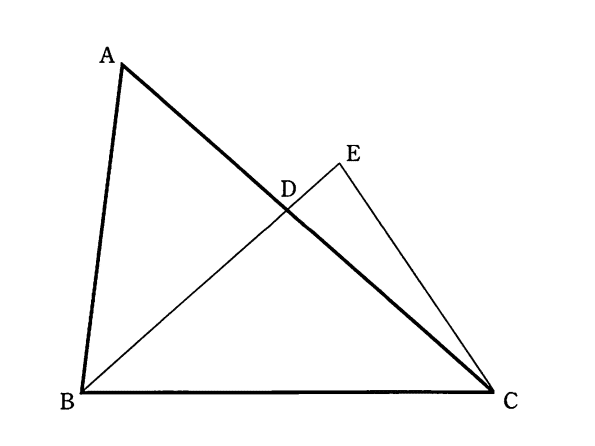
点Dは∠ABCの二等分線と辺ACとの交点、点Eは線分BDの延長上にあり、CD=CEです。
(1)△ABD∽△CBE であることを証明します。
【証明】
△ABDと△CBEにおいて、
仮定より、∠ABD=∠CBE ・・・①
△CDEで、仮定より、CD=CEであるから
二等辺三角形の底角は等しいので、
∠CDE=∠CED ・・・②
対頂角は等しいので、
∠ADB=∠CDE ・・・③
②、③より、∠ADB=∠CED ・・・④
①、④より、2組の角がそれぞれ等しいので、
△ABD∽△CBE
【証明終】
上記の証明は、解答の一例です。
(2)AB=4㎝、BC=5㎝、CA=6cmのとき
(ア)CEの長さを求めます。
角の二等分線の性質より、
BA:BC=AD:CD が成り立ちます。
したがって、AD:CD=4:5です。
いま、$${CE=x}$$とすると、$${CD=x}$$、$${AD=(6-x)}$$となるので、
$${(6-x):x=4:5}$$ から、
$${4x=5(6-x)}$$
$${4x=30-5x}$$
$${9x=30}$$
$${x=\frac {10} {3}}$$
したがって、CE=$${\frac {10} {3}}$$ となります。
(イ)△ABDの面積は、△CDEの面積の何倍になるか、を求めます。
(ア)より、AD:CD=4:5であることから、
△ABCの面積を9Sとすると、△ABD=4S、△BCD=5Sとなります。
また、(1)より、△ABD∽△CBEで、相似比は4:5なので、
面積比は、16:25です。△ABD=4Sのとき、△CBE=$${\frac {25S} {4}}$$
△CDE=△CBE-△BCD=$${\frac {25S} {4}}$$-5S=$${\frac {5S} {4}}$$
したがって、4S÷$${\frac {5S} {4}}$$=$${\frac {16} {5}}$$
$${\frac {16} {5}}$$倍となります。
6⃣ 数字の規則性の問題です(1~3年)
一定の規則で、数字が並べられます。

規則性の問題としては、それほど珍しくないタイプです。
(1)5回目について
(ア)新たに書く自然数の個数は、17~25の9個です。
(イ)正方形の右下に書く数字は、21です。
(2)は空欄補充形式の問題です。
n回目の作業で書く最も大きい数字は、(ア)$${n^2}$$です。
(n-1)回目の作業で書く最も大きい数字は、(イ)$${(n-1)^2}$$です。
したがって、n回目の作業では、$${n^2-(n-1)^2=2n-1}$$ (ウ)$${(2n-1)}$$個の連続した自然数を書くことになります。
以上から、n回目の作業で、正方形の右下に書く自然数は、(エ)$${n^2-n+1}$$ になります。
(エ)の求め方はいろいろありますが、縦1列の個数がn個なので、$${n^2-n}$$とすると1列すべてなくなってしまうことから、+1して$${n^2-n+1}$$と求める方法など、中1の文字式で扱うやり方がわかりやすいでしょう。
(※)高校生なら、右下の自然数を階差数列にして求めることもできます。
初項が1、階差数列が2nですから、
$${S=1+\displaystyle\sum_{k=1}^{n-1} 2k}$$
$${S=1+n(n-1)}$$
$${S=n^2-n+1}$$
(3)10回目の作業について、
(ア)右下の自然数は、$${10^2-10+1=91}$$ です
(イ)新たに書く自然数の和は、82~100までの自然数の和です。
時間が残っていれば、「日向君の強引なドリブル」のような解き方をしていても構いませんが、それでは高校入学後に若林君に止められ(以下略
82+83+・・・+99+100
+)100+99+・・・+83+82
のように、縦に順序を逆にした足し算の式を並べて加えると
182が19組できます。
同じ和が2つありますので、2で割れば、
$${(82+100)×19÷2=1729}$$
となります。
(※)これも高校生は等差数列の和の公式で解けます(上記もその一例)。
以上です。極端な「難問」はなかったので、平均点はそれなりになりそうです。昨年よりもやや易化したでしょうか。
